【LeetCode:1954. 收集足够苹果的最小花园周长 | 等差数列 + 公式推导】

发布时间：2023年12月24日

在这里插入图片描述

🚀 算法题 🚀

🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样?
🌲 作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯

🚀 算法题 🚀

在这里插入图片描述

在这里插入图片描述

🍔 目录

🚩 题目链接

? 题目描述

给你一个用无限二维网格表示的花园，每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。

你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ，且每条边都与两条坐标轴之一平行。

给你一个整数 neededApples ，请你返回土地的 最小周长 ，使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。

|x| 的值定义为：

如果 x >= 0 ，那么值为 x
如果 x < 0 ，那么值为 -x

示例 1：
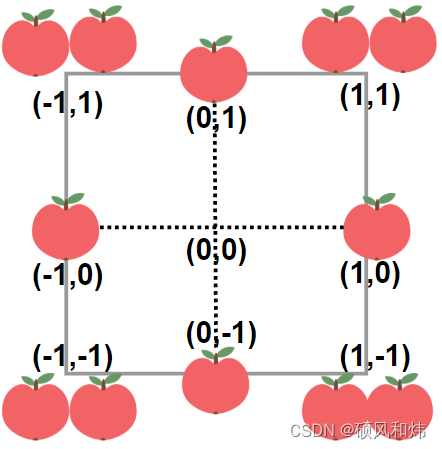
在这里插入图片描述

输入：neededApples = 1
输出：8
解释：边长长度为 1 的正方形不包含任何苹果。
但是边长为 2 的正方形包含 12 个苹果（如上图所示）。
周长为 2 * 4 = 8 。
示例 2：

输入：neededApples = 13
输出：16
示例 3：

输入：neededApples = 1000000000
输出：5040

提示：

1 <= neededApples <= 1015

🌟 求解思路&实现代码&运行结果

? 等差数列 + 公式推导

🥦 求解思路

  1. 通过等差数列求和公式计算正方形中包含的苹果个数，具体公式推导参考如下的题解，不做过多的解释。

  2. 力扣官方题解

  3. 实现代码如下所示：

🥦 实现代码
class Solution {
    public long minimumPerimeter(long neededApples) {
        long x = 1;
        while (2 * x * (x + 1) * (2 * x + 1) < neededApples) {
            ++x;
        }
        return 8 * x;
    }
}
🥦 运行结果

在这里插入图片描述

💬 共勉

最后，我想和大家分享一句一直激励我的座右铭，希望可以与大家共勉！

在这里插入图片描述

在这里插入图片描述

文章来源:https://blog.csdn.net/Coder_ljw/article/details/135180327
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章