【白话机器学习的数学】读书笔记(4)评估(评估已建立的模型)
四、评估(评估已建立的模型)
目录
1.评估什么
在进行回归和分类时,为了进行预测,我们定义了函数 f θ ( x ) f_θ(x) fθ?(x),然后根据训练数据求出了函数的参数 θ。最后求出了参数更新表达式,然后不断重复更新参数。
但是我们不要忘了我们的目标是通过预测函数得到预测值。所以我们要评估的就是预测函数 f θ ( x ) f_θ(x) fθ?(x)的正确性。
2.交叉验证
把全部训练数据分为测试数据和训练数据的做法称为交叉验证。
1 回归问题的验证
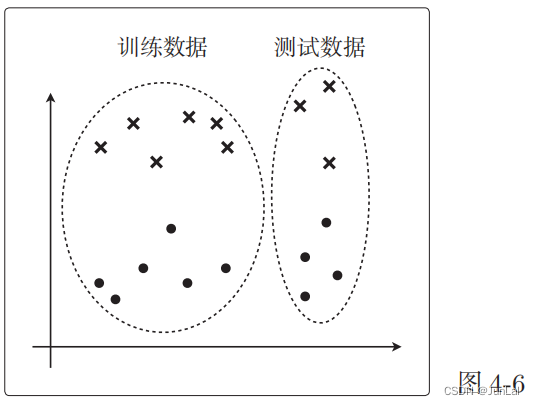
把获取的全部训练数据分成两份:一份用于测试,一份用于训练。然后用前者来评估模型。
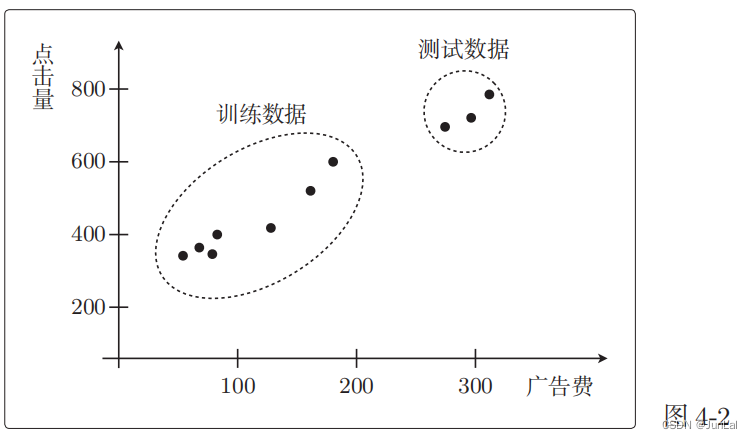
用一次函数预测的效果 f θ ( x ) = θ 0 + θ 1 x ? f_θ(x) = θ_0 + θ_1x^* fθ?(x)=θ0?+θ1?x?:
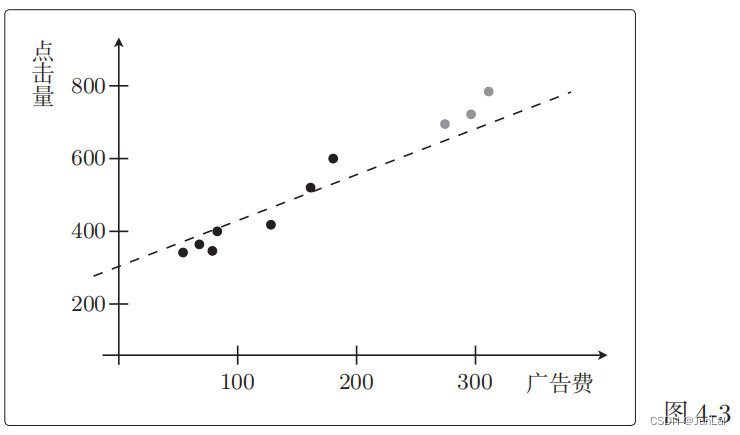
二次函数预测的效果:
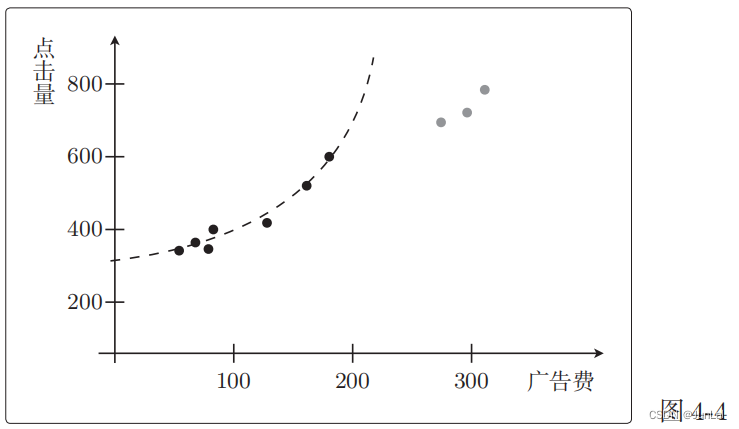
那么,二次函数是只有对训练数据才是正确的。
如果只看训练数据,那么二次函数比一次函数拟合得更好。但是,如果将测试数据也考虑进来,那么二次函数就完全不行了。
模型评估就是像这样检查训练好的模型对测试数据的拟合情况。
评估:对于回归的情况,只要在训练好的模型上计算测试数据的误差的平方,再取其平均值就可以了。假设测试数据有 n 个,那么可以这样计算。
M
S
E
=
1
n
∑
i
=
1
n
(
y
(
i
)
?
f
θ
(
x
(
i
)
)
)
2
MSE = \frac1n\sum_{i=1}^n\left(y^{(i)}-f_\theta(\boldsymbol{x}^{(i)})\right)^2
MSE=n1?i=1∑n?(y(i)?fθ?(x(i)))2
-
这个值被称为均方误差或者 MSE,全称 Mean Square Error。
-
对于预测点击量的回归问题来说,y(i) 就是点击量,而 x(i) 是广告
费或广告版面的大小
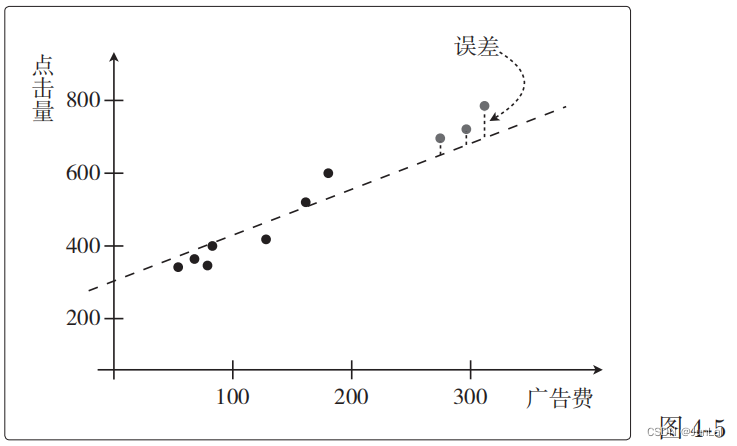
其实,回归的目标函数也是误差函数。因为他们要做的事情是一致的,为了让误差函数的值变小而更新参数时所做的事情是一样的。
2 分类问题的验证
首先还是数据的分配:
对于分类的结果有以下几种情况:
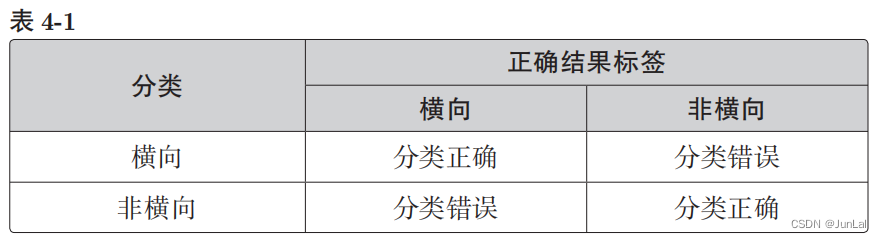
设横向的情况为正、非横向的情况为负,那么一般来说,二分类的结果可以用这张表来表示:
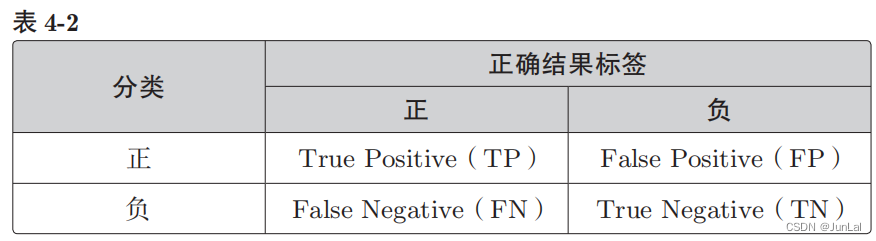
即分类结果为正的情况是 Positive、为负的情况是 Negative。分类成功为 True、分类失败为 False。
那么精度Accuracy就可以表示成:
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
F
P
+
F
N
+
T
N
Accuracy=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{FP}+\mathrm{FN}+\mathrm{TN}}
Accuracy=TP+FP+FN+TNTP+TN?
假如 100 个数据中 80 个被正确地分类了,那么精度就是:
A
c
c
u
r
a
c
y
=
80
100
=
0.8
Accuracy = \frac{80}{100} = 0.8
Accuracy=10080?=0.8
3 精确率和召回率
假设有 100 个数据,其中 95 个是 Negative。那么,哪怕出现模型把数据全部分类为 Negative 的极端情况,Accuracy 值也为 0.95,也就是说模型的精度是 95%
不管精度多高,一个把所有数据都分类为 Negative 的模型,不能算作一个好模型。
所以,我们要引入别的指标。
1.精确率Precision
P r e c i s i o n = T P T P + F P Precision=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} Precision=TP+FPTP?
- 这个指标只关注 TP 和 FP(只关注分类为Positive的部分)
- 它的含义是在被分类为 Positive 的数据中,实际就是 Positive 的数据所占的比例
- 这个值越高,说明分类错误越少。假设TP = 1,FP = 2,那么Precision = 33.3%。虽然被分类为 Positive 的数据有 3 个,但其中只有 1 个是分类正确的。所以计算得出的精确率很低。
2.召回率Recall
R e c a l l = T P T P + F N Recall=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} Recall=TP+FNTP?
- 这个指标只关注 TP 和 FN
- 它的含义是在Positive 数据中,实际被分类为 Positive 的数据所占的比例
- 这个值越高,说明被正确分类的数据越多
- 假设TP = 1,FN = 4(FN是数据是Positive但被分类为Negative的个数),那么Recall = 1/5。
- 虽然 Positive 数据共有 5 个,但只有 1 个被分类为 Positive。所以计算得出的召回率也很低。
4 F值
精确率和召回率会一个高一个低,这时候就需要了评定综合性能的指标 F 值。
F
m
e
a
s
u
r
e
=
2
1
P
r
e
c
i
s
i
o
n
+
1
R
e
c
a
l
l
=
2
?
P
r
e
c
i
s
i
o
n
?
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
Fmeasure=\frac2{\frac1{Precision}+\frac1{Recall}} = \frac{2\cdot Precision\cdot Recall}{Precision+Recall}
Fmeasure=Precision1?+Recall1?2?=Precision+Recall2?Precision?Recall?
精确率和召回率只要有一个低,就会拉低 F 值。
有时称 F 值为 F1 值会更准确,这一点需要注意。有的时候含义相同,有时候却并不相同。除 F1 值之外,还有一个带权重的 F 值指标:
W
e
i
g
h
t
e
d
F
m
e
a
s
u
r
e
=
(
1
+
β
2
)
?
P
r
e
c
i
s
i
o
n
?
R
e
c
a
l
l
β
2
?
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
WeightedFmeasure=\frac{(1+\beta^2)\cdot Precision\cdot Recall}{\beta^2\cdot Precision+Recall}
WeightedFmeasure=β2?Precision+Recall(1+β2)?Precision?Recall?
- 我们可以认为 F 值指的是带权重的 F 值,当权重为 1 时才是刚才介绍的 F1 值。
- F1 值在数学上是精确率和召回率的调和平均值。
之前介绍的精确率和召回率都是以 TP 为主进行计算的,也能以 TN 为主:
Precision
=
T
N
T
N
+
F
N
Recall
=
T
N
T
N
+
F
P
\begin{aligned} \text{Precision}& =\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FN}} \\ \text{Recall}& =\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}} \end{aligned}
PrecisionRecall?=TN+FNTN?=TN+FPTN??
我们选择TP和TN的一个重要依据是当数据不平衡时,使用数量少的那个会更好。
5 K折交叉验证
- 把全部训练数据分为 K 份
- 将 K ? 1 份数据用作训练数据,剩下的 1 份用作测试数据
- 每次更换训练数据和测试数据,重复进行 K 次交叉验证
- 最后计算 K 个精度的平均值,把它作为最终的精度
假如我们要进行 4 折交叉验证,那么就会这样测量精度:
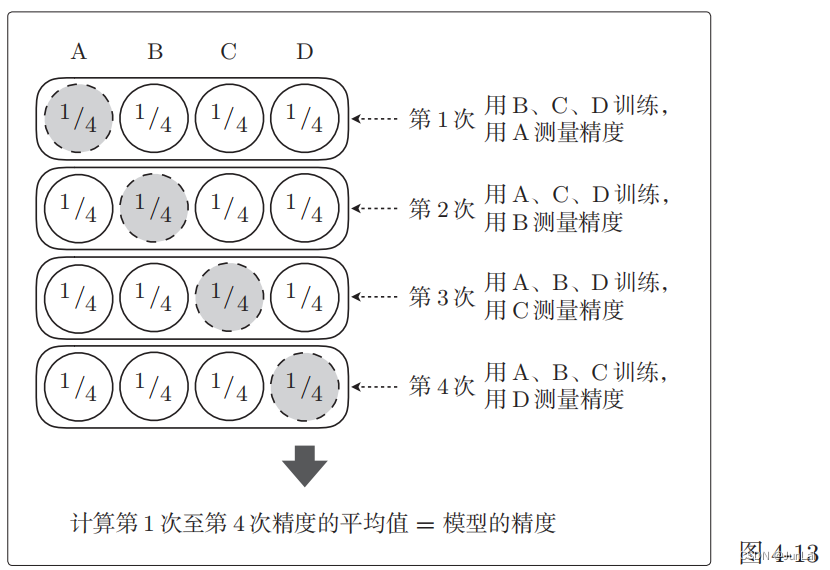
不切实际地增加 K 值会非常耗费时间,所以我们必须要确定一个合适的 K 值
3.正则化
模型只能拟合训练数据的状态被称为过拟合,英文是 overfitting。
避免过拟合的几种方法:
- 增加全部训练数据的数量
- 使用简单的模型
- 正则化
1 正则化的方法
回归的目标函数:
E
(
θ
)
=
1
2
∑
i
=
1
n
(
y
(
i
)
?
f
θ
(
x
(
i
)
)
)
2
E(\boldsymbol{\theta})=\frac12\sum_{i=1}^n\left(y^{(i)}-f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})\right)^2
E(θ)=21?i=1∑n?(y(i)?fθ?(x(i)))2
我们要向这个目标函数增加下面这样的正则化项:
R
(
θ
)
=
λ
2
∑
j
=
1
m
θ
j
2
R(\boldsymbol{\theta})=\frac\lambda2\sum_{j=1}^m\theta_j^2
R(θ)=2λ?j=1∑m?θj2?
就变成了:
E
(
θ
)
=
1
2
∑
i
=
1
n
(
y
(
i
)
?
f
θ
(
x
(
i
)
)
)
2
+
R
(
θ
)
=
1
2
∑
i
=
1
n
(
y
(
i
)
?
f
θ
(
x
(
i
)
)
)
2
+
λ
2
∑
j
=
1
m
θ
j
2
\begin{aligned} E(\boldsymbol{\theta})& \begin{aligned}=\frac{1}{2}\sum_{i=1}^{n}\left(y^{(i)}-f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})\right)^2+R(\boldsymbol{\theta})\end{aligned} \\ &=\frac12\sum_{i=1}^n\left(y^{(i)}-f_\theta(\boldsymbol{x}^{(i)})\right)^2+\frac\lambda2\sum_{j=1}^m\theta_j^2 \end{aligned}
E(θ)?=21?i=1∑n?(y(i)?fθ?(x(i)))2+R(θ)?=21?i=1∑n?(y(i)?fθ?(x(i)))2+2λ?j=1∑m?θj2??
我们要对这个新的目标函数进行最小化,这种方法就称为正则化。
-
一般来说不对 $θ_0 应用正则化。所以仔细看会发现 ? j ? 的取值是从 1 开始的。 应用正则化。所以仔细看会发现 *j* 的取值是从 1 开始的。 应用正则化。所以仔细看会发现?j?的取值是从1开始的。θ_0$ 这种只有参数的项称为偏置项,一般不对它进行正则化。
-
假如预测函数的表达式为 f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 fθ(x) = θ_0 + θ_1x + θ_2x^2 fθ(x)=θ0?+θ1?x+θ2?x2,那么 m = 2 就意味着正则化的对象参数为 θ1 和 θ2。
-
λ 是决定正则化项影响程度的正的常数。需要我们自行确定。
2 正则化的效果
把目标函数分成两个部分:
C
(
θ
)
=
1
2
∑
i
=
1
n
(
y
(
i
)
?
f
θ
(
x
(
i
)
)
)
2
R
(
θ
)
=
λ
2
∑
j
=
1
m
θ
j
2
\begin{aligned} &C(\boldsymbol{\theta}) =\frac12\sum_{i=1}^n\left(y^{(i)}-f_\theta(\boldsymbol{x}^{(i)})\right)^2 \\ &R(\boldsymbol{\theta}) =\frac\lambda2\sum_{j=1}^m\theta_j^2 \end{aligned}
?C(θ)=21?i=1∑n?(y(i)?fθ?(x(i)))2R(θ)=2λ?j=1∑m?θj2??
- C(θ) 是本来就有的目标函数项,R(θ) 是正则化项
C(θ) 和 R(θ) 相加之后就是新的目标函数,所以我们实际地把这两个函数的图形画出来。
参数太多就画不出图来了,所以这里我们只关注 θ1。而且为了更加易懂,先不考虑 λ。
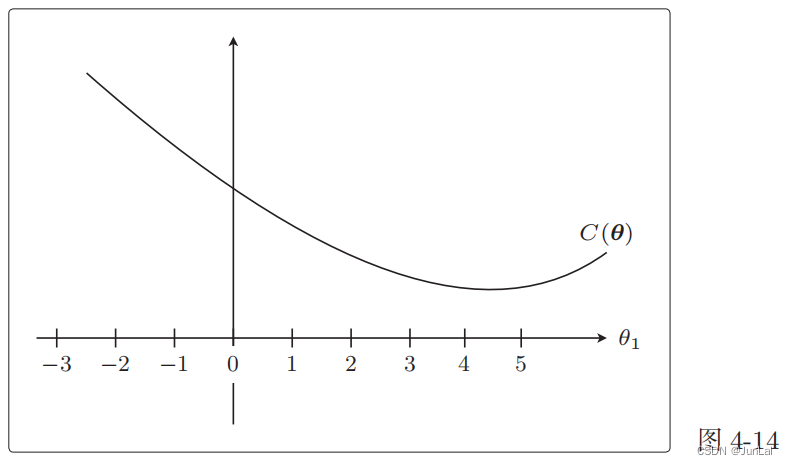
从这个目标函数在没有正则化项时的形状来看, θ 1 = 4.5 θ_1 = 4.5 θ1?=4.5 附近是最小值。
接下来是 R(θ),它就相当于
1
2
θ
1
2
\frac{1}{2}\theta_1^2
21?θ12?,所以是过原点的简单二次函数。
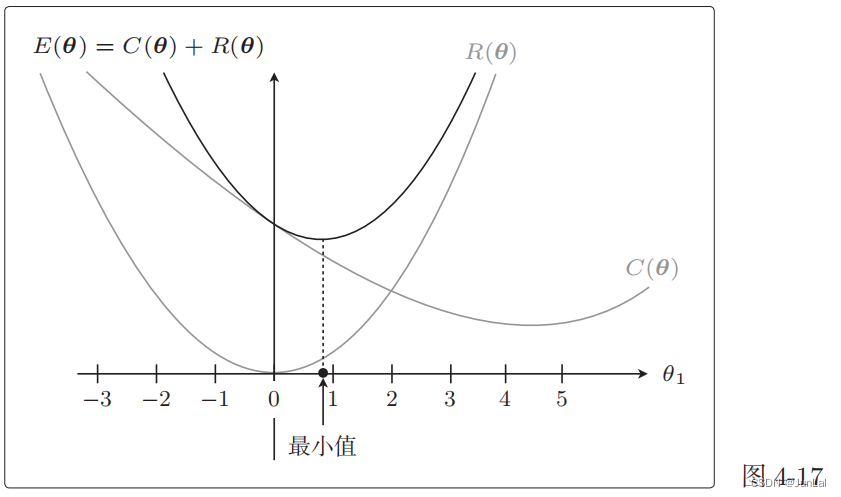
实际的目标函数是这两个函数之和 E ( θ ) = C ( θ ) + R ( θ ) E(θ) = C(θ) + R(θ) E(θ)=C(θ)+R(θ)
与加正则化项之前相比, θ 1 θ_1 θ1? 更接近 0 了。本来是在 θ 1 = 4.5 θ_1 = 4.5 θ1?=4.5 处最小,现在是在 θ 1 = 0.9 θ_1 = 0.9 θ1?=0.9 处最小,的确更接近 0 了。
这就是正则化的效果。它可以防止参数变得过大,有助于参数接近较小的值。虽然我们只考虑了 θ 1 θ_1 θ1?,但其他 θ j θ_j θj? 参数的情况也是类似的。
参数的值变小,意味着该参数的影响也会相应地变小。比如,有这样的一个预测函数
f
θ
(
x
)
f_θ(x)
fθ?(x)。
f
θ
(
x
)
=
θ
0
+
θ
1
x
+
θ
2
x
2
f_{\boldsymbol{\theta}}(\boldsymbol{x})=\theta_0+\theta_1x+\theta_2x^2
fθ?(x)=θ0?+θ1?x+θ2?x2
极端一点,假设
θ
2
=
0
θ_2 = 0
θ2?=0,这个表达式就从二次变为一次了。这就意味着本来是曲线的预测函数变为直线了。
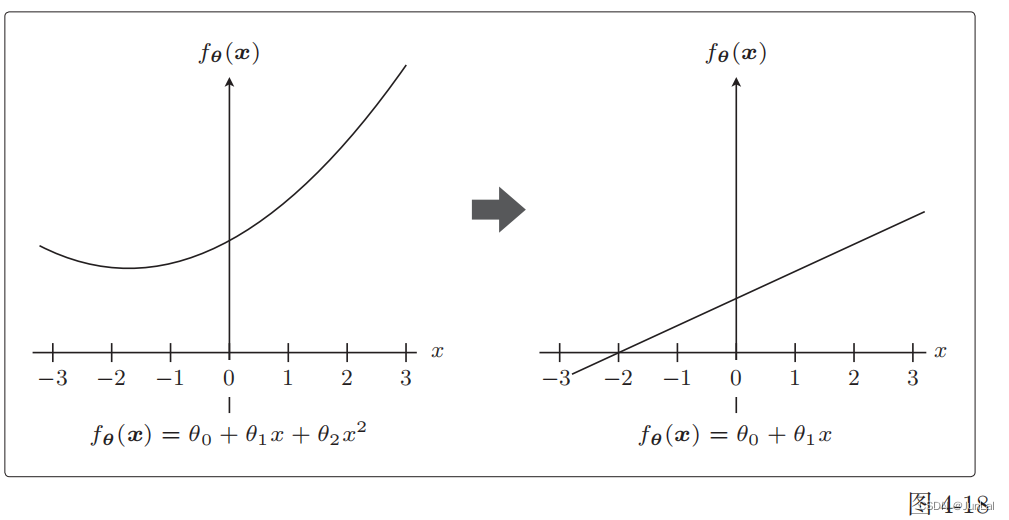
这正是通过减小不需要的参数的影响,将复杂模型替换为简单模型来防止过拟合的方式。
为了防止参数的影响过大,在训练时要对参数施加这样的一些惩罚。
λ 是可以控制正则化惩罚的强度。
- 令 λ = 0,那就相当于不使用正则化
- λ 越大,正则化的惩罚也就越严厉
3 分类的正则化
前面讨论的是回归的情况,分类也是可以正则化的。
逻辑回归的目标函数:
log
?
L
(
θ
)
=
∑
i
=
1
n
(
y
(
i
)
log
?
f
θ
(
x
(
i
)
)
+
(
1
?
y
(
i
)
)
log
?
(
1
?
f
θ
(
x
(
i
)
)
)
)
\log L(\boldsymbol{\theta})=\sum_{i=1}^n\left(y^{(i)}\log f_\theta(\boldsymbol{x}^{(i)})+(1-y^{(i)})\log(1-f_\theta(\boldsymbol{x}^{(i)}))\right)
logL(θ)=i=1∑n?(y(i)logfθ?(x(i))+(1?y(i))log(1?fθ?(x(i))))
分类也是在这个目标函数中增加正则化项就行了:
log
?
L
(
θ
)
=
?
∑
i
=
1
n
(
y
(
i
)
log
?
f
θ
(
x
(
i
)
)
+
(
1
?
y
(
i
)
)
log
?
(
1
?
f
θ
(
x
(
i
)
)
)
)
+
λ
2
∑
j
=
1
m
θ
j
2
\begin{aligned}\log L(\theta)&=-\sum_{i=1}^n\left(y^{(i)}\log f_\theta(x^{(i)})+(1-y^{(i)})\log(1-f_\theta(x^{(i)}))\right)+\frac{\lambda}{2}\sum_{j=1}^m\theta_j^2\end{aligned}
logL(θ)?=?i=1∑n?(y(i)logfθ?(x(i))+(1?y(i))log(1?fθ?(x(i))))+2λ?j=1∑m?θj2??
- 对数似然函数本来以最大化为目标。但是,这次我想让它变成和回归的目标函数一样的最小化问题,所以加了负号。
4 包含正则化项的表达式的微分
1 回归加入正则化后的更新表达式
目标函数的形式变了,参数更新的表达式也会变,不过只要再把正则化项的部分也微分。
E
(
θ
)
=
C
(
θ
)
+
R
(
θ
)
?
E
(
θ
)
?
θ
j
=
?
C
(
θ
)
?
θ
j
+
?
R
(
θ
)
?
θ
j
E(\boldsymbol{\theta})=C(\boldsymbol{\theta})+R(\boldsymbol{\theta})\\ \frac{\partial E(\boldsymbol{\theta})}{\partial\theta_j}=\frac{\partial C(\boldsymbol{\theta})}{\partial\theta_j}+\frac{\partial R(\boldsymbol{\theta})}{\partial\theta_j}
E(θ)=C(θ)+R(θ)?θj??E(θ)?=?θj??C(θ)?+?θj??R(θ)?
第一部分:
?
C
(
θ
)
?
θ
j
=
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
(
i
)
\frac{\partial C(\boldsymbol{\theta})}{\partial\theta_j}=\sum_{i=1}^n\Big(f_\theta(\boldsymbol{x}^{(i)})-y^{(i)}\Big)x_j^{(i)}
?θj??C(θ)?=i=1∑n?(fθ?(x(i))?y(i))xj(i)?
第二部分:
R
(
θ
)
=
λ
2
∑
j
=
1
m
θ
j
2
=
λ
2
θ
1
2
+
λ
2
θ
2
2
+
?
+
λ
2
θ
m
2
?
R
(
θ
)
?
θ
j
=
λ
θ
j
\begin{aligned} R(\boldsymbol{\theta})& =\frac\lambda2\sum_{j=1}^m\theta_j^2 \\ &=\frac\lambda2\theta_1^2+\frac\lambda2\theta_2^2+\cdots+\frac\lambda2\theta_m^2 \end{aligned} \\ \frac{\partial R(\boldsymbol{\theta})}{\partial\theta_j}=\lambda\theta_j
R(θ)?=2λ?j=1∑m?θj2?=2λ?θ12?+2λ?θ22?+?+2λ?θm2???θj??R(θ)?=λθj?
整合:
?
E
(
θ
)
?
θ
j
=
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
(
i
)
+
λ
θ
j
\frac{\partial E(\boldsymbol{\theta})}{\partial\theta_j}=\sum_{i=1}^n\left(f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})-y^{(i)}\right)x_j^{(i)}+\lambda\theta_j
?θj??E(θ)?=i=1∑n?(fθ?(x(i))?y(i))xj(i)?+λθj?
所以加入了正则化项的参数更新表达式:
θ
0
:
=
θ
0
?
η
(
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
(
i
)
)
θ
j
:
=
θ
j
?
η
(
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
(
i
)
+
λ
θ
j
)
(
j
>
0
)
\begin{aligned}\theta_0&:=\theta_0-\eta\left(\sum_{i=1}^n\left(f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})-y^{(i)}\right)x_j^{(i)}\right)\\\\\theta_j&:=\theta_j-\eta\left(\sum_{i=1}^n\left(f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})-y^{(i)}\right)x_j^{(i)}+\lambda\theta_j\right)&(j>0)\end{aligned}
θ0?θj??:=θ0??η(i=1∑n?(fθ?(x(i))?y(i))xj(i)?):=θj??η(i=1∑n?(fθ?(x(i))?y(i))xj(i)?+λθj?)?(j>0)?
一般不对
θ
0
θ_0
θ0? 应用正则化。
R
(
θ
)
R(θ)
R(θ) 对
θ
0
θ_0
θ0? 微分的结果为 0,所以 j = 0 时表达式中的
λ
θ
j
λθ_j
λθj? 就消失了。
2 逻辑回归包含正则化项的更新表达式
其实和回归的处理是一样的。
C
(
θ
)
=
?
∑
i
=
1
n
(
y
(
i
)
log
?
f
θ
(
x
(
i
)
)
+
(
1
?
y
(
i
)
)
log
?
(
1
?
f
θ
(
x
(
i
)
)
)
)
R
(
θ
)
=
λ
2
∑
j
=
1
m
θ
j
2
E
(
θ
)
=
C
(
θ
)
+
R
(
θ
)
\begin{aligned} &C(\boldsymbol{\theta}) \begin{aligned}=-\sum_{i=1}^n\left(y^{(i)}\log f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})+(1-y^{(i)})\log(1-f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)}))\right)\end{aligned} \\ &R(\boldsymbol{\theta}) =\frac\lambda2\sum_{j=1}^m\theta_j^2 \\ &E(\boldsymbol{\theta}) =C(\boldsymbol{\theta})+R(\boldsymbol{\theta}) \end{aligned}
?C(θ)=?i=1∑n?(y(i)logfθ?(x(i))+(1?y(i))log(1?fθ?(x(i))))?R(θ)=2λ?j=1∑m?θj2?E(θ)=C(θ)+R(θ)?
然后求微分:
?
E
(
θ
)
?
θ
j
=
?
C
(
θ
)
?
θ
j
+
?
R
(
θ
)
?
θ
j
\frac{\partial E(\boldsymbol{\theta})}{\partial\theta_j}=\frac{\partial C(\boldsymbol{\theta})}{\partial\theta_j}+\frac{\partial R(\boldsymbol{\theta})}{\partial\theta_j}
?θj??E(θ)?=?θj??C(θ)?+?θj??R(θ)?
现在考虑的是最小化问题,所以要注意在前面加上负号。也就是要进行符号的反转。
?
C
(
θ
)
?
θ
j
=
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
(
i
)
?
R
(
θ
)
?
θ
j
=
λ
θ
j
\frac{\partial C(\boldsymbol{\theta})}{\partial\theta_j}=\sum_{i=1}^n\left(f_\theta(\boldsymbol{x}^{(i)})-y^{(i)}\right)x_j^{(i)} \\ \frac{\partial R(\boldsymbol{\theta})}{\partial\theta_j}=\lambda\theta_j
?θj??C(θ)?=i=1∑n?(fθ?(x(i))?y(i))xj(i)??θj??R(θ)?=λθj?
所以更新表达式为:
$$
$$
θ 0 : = θ 0 ? η ( ∑ i = 1 n ( f θ ( x ( i ) ) ? y ( i ) ) x j ( i ) ) θ j : = θ j ? η ( ∑ i = 1 n ( f θ ( x ( i ) ) ? y ( i ) ) x j ( i ) + λ θ j ) ( j > 0 ) \begin{aligned}\theta_0&:=\theta_0-\eta\left(\sum_{i=1}^n\left(f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})-y^{(i)}\right)x_j^{(i)}\right)\\\\\theta_j&:=\theta_j-\eta\left(\sum_{i=1}^n\left(f_{\boldsymbol{\theta}}(\boldsymbol{x}^{(i)})-y^{(i)}\right)x_j^{(i)}+\lambda\theta_j\right)(j>0)\end{aligned} θ0?θj??:=θ0??η(i=1∑n?(fθ?(x(i))?y(i))xj(i)?):=θj??η(i=1∑n?(fθ?(x(i))?y(i))xj(i)?+λθj?)(j>0)?
上面介绍的方法是L2正则化。
5 L2正则化 VS L1正则化
L2 正则化方法之外,还有 L1 正则化方法。它的正则化项 R 是:
R
(
θ
)
=
λ
∑
i
=
1
m
∣
θ
i
∣
R(\boldsymbol{\theta})=\lambda\sum_{i=1}^m|\theta_i|
R(θ)=λi=1∑m?∣θi?∣
对比:
- L1 正则化的特征是被判定为不需要的参数会变为 0,从而减少变量个数。而 L2 正则化不会把参数变为 0。
- L2 正则化会抑制参数,使变量的影响不会过大,而 L1 会直接去除不要的变量。
没有绝对的好坏,使用那种正则化取决于实际问题。
4.学习曲线
展示了数据数量和精度的图称为学习曲线。
1 欠拟合
欠拟合是没有拟合训练数据的状态,用英文说是 underfitting。
2 区分欠拟合和过拟合:
以数据的数量为横轴、以精度为纵轴,然后把用于训练的数据和用于测试的数据画成图:
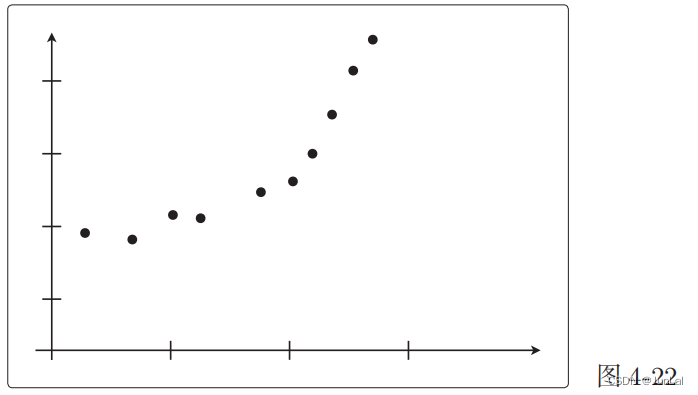
a.欠拟合
当目标函数很简单, f θ ( x ) f_\theta(x) fθ?(x)为一次函数时:
- 只选用2个数据进行训练
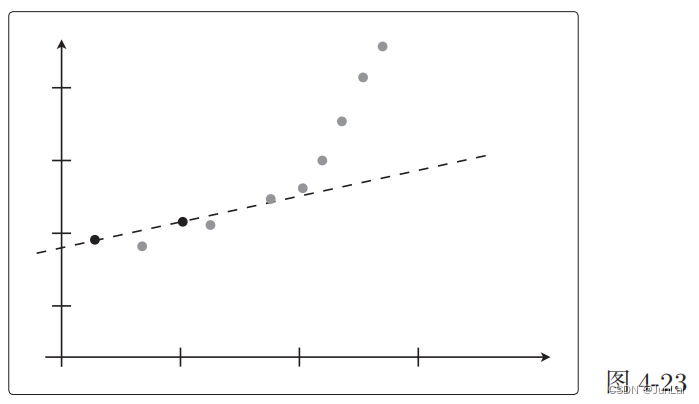
在这个状态下,2 个用来训练的点都完美拟合,误差为 0。
- 把 10 个数据都用来训练
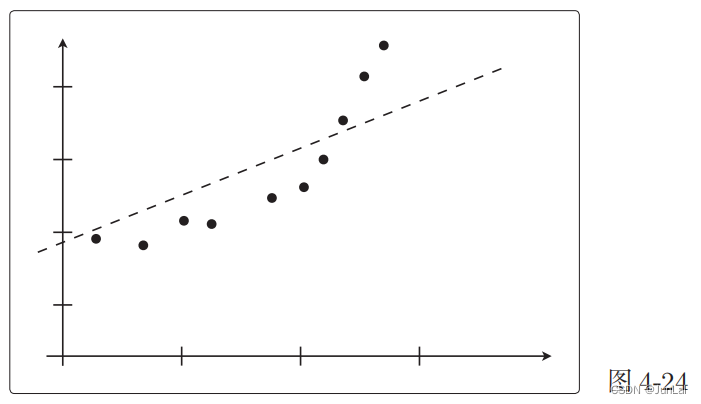
在这种情况下,误差已经无法为 0且很大。
模型过于简单,那么随着数据量的增加,误差也会一点点变大。也就是精度会一点点下降。
以数据的数量为横轴、以精度为纵轴的图:
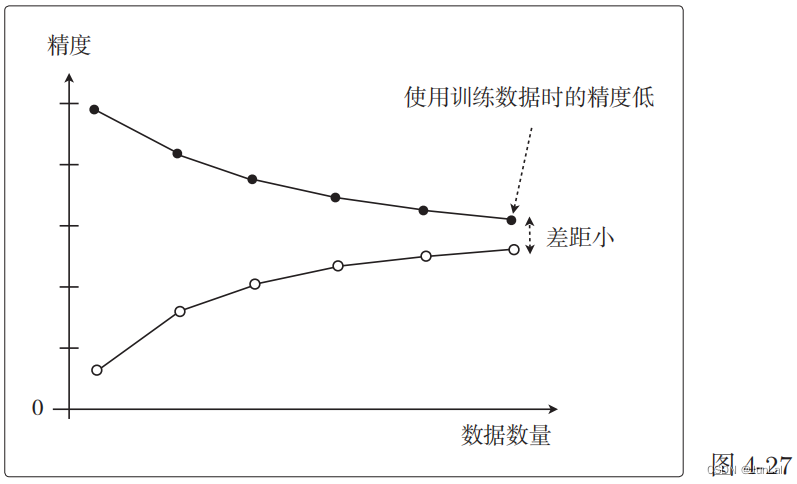
用测试数据先评估根据 2 个训练数据训练好的模型,再评估根据10 个训练数据训练好的模型,我们可以得出结论:
- 训练数据较少时训练好的模型难以预测未知的数据(测试数据),所以精度很低;相反,训练数据变多时,预测精度就会一点点地变高
两份数据的精度用图来展示后,如果是这种形状,就说明出现了欠拟合的状态。也叫作高偏差。
b.过拟合
过拟合的情况下,图是这样的。这也叫作高方差:
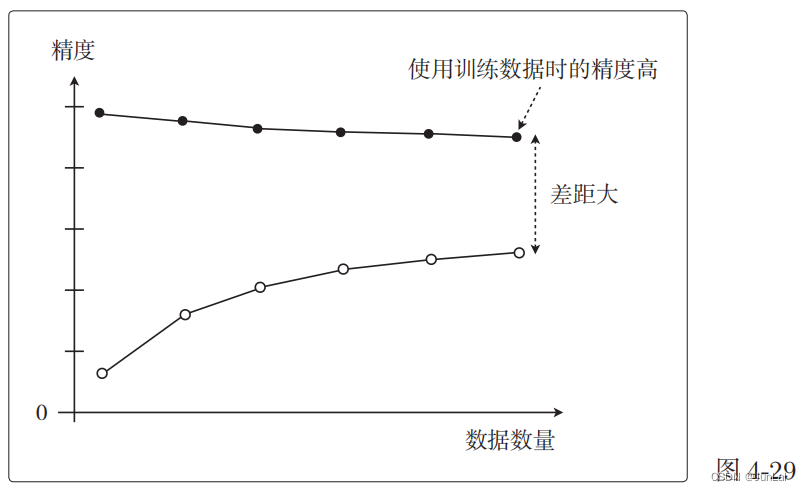
随着数据量的增加,使用训练数据时的精度一直很高,而使用测试数据时的精度一直没有上升到它的水准。
只对训练数据拟合得较好,这就是过拟合的特征。
3 总结
像这样展示了数据数量和精度的图称为学习曲线。
通过学习曲线判断出是过拟合还是欠拟合之后,就可以采取相应的对策以便改进模型。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 程序员必备的面试技巧
- CSC行业合作项目|政府公务员赴英国南安普顿大学访学交流
- 读书笔记-《数据结构与算法》-摘要5[归并排序]
- 在加载第三方库过程中,无法加载到库的问题(使用readelf, patchelf命令)
- DDD领域驱动设计(三)
- STM32CubeMX教程17 DAC - 输出三角波/噪声波
- 用标记接口定义类型
- 2023.1.4 使用python的update方法快速将字典数据补齐
- 【VTKExamples::Filtering】第一期 TestContoursFromPolyData
- 基于Spring Boot、Mybatis、Redis和Layui的企业电子招投标系统源码实现与立项流程