AcWing.898.数字三角形（线性DP）

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

输入格式

第一行包含整数?n，表示数字三角形的层数。

接下来?n?行，每行包含若干整数，其中第?i?行表示数字三角形第?i?层包含的整数。

输出格式

输出一个整数，表示最大的路径数字和。

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

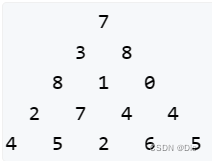
?我们可以把三角形划分成以下形式，这样三角形中每个点可以由左上或是右上到达，即(i,j)可以由(i-1,j-1)到达也可以由(i-1,j)到达

?

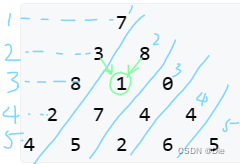
根据题意，让f[i][j]表示所有从起点到达(i,j)的路径的最大值，用a[i][j]代表(i,j)点的数值，得状态转移方程

????????????????????????f[ i ][ j?] = max(f[ i-1, j-1 ] + a[ i ][ j ]，f[ i-1 ][ j ] + a[ i ][ j ]);

写出代码：

#include<iostream>
using namespace std;
const int N = 505;
const int INF = -0x3f3f3f3f;

int f[N][N];	//f[i][j]代表从起点到(i,j)的最大路径
int a[N][N];	//存每个点的数值
int n;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);

	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= i; j++) {
			cin >> a[i][j];
		}
	}

	for (int i = 0; i <= n; i++) {			
		for (int j = 0; j <= i + 1; j++) {	//初始化为负无穷的范围要涵盖到所有点的左上和右上点
			f[i][j] = INF;					//初始化为负无穷使状态转移方程不会被没有读取的点扰乱
		}
	}

	f[1][1] = a[1][1];		//起点设置为其本身数值

	for (int i = 2; i <= n; i++) {
		for (int j = 1; j <= i; j++) {
			f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);	//状态转移方程
		}
	}

	int ans = INF;

	for (int j = 1; j <= n; j++) {	//如果从上而下进行dp，到最后会得到三角形最后一排的n个最大值，从里面取最大
		ans = max(ans, f[n][j]);
	}

	cout << ans;
	return 0;
}

?如果想要删去最后一层答案取最大值的循环，可以对三角形自下往上进行dp。