机器学习_通过梯度下降找到最佳参数

---

训练机器要有正确的方向

所谓训练机器，也称拟合的过程，也就是确定模型内部参数的过程。具体到线性模型，也就是确定y’=wx+b 函数中的w和b。

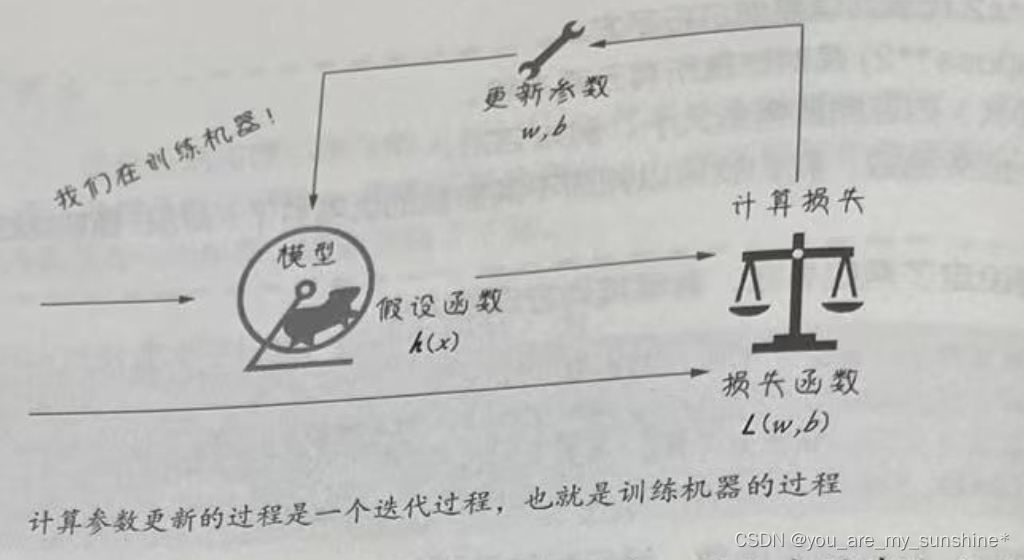
对于线性回归来说，针对损失函数的梯度下降(gradient descent )方法可以使猜测沿着正确的方向前进，因此总能找到比起上一次猜测时误差更小的w和b组合。

梯度下降可以说是整个机器学习的精髓，堪称机器学习之魂。在我们身边发生的种种机器学习和深度学习的奇迹，归根结底都是拜梯度下降所赐。

凸函数确保有最小损失点

只是前进的方向对了，这还不够，还有另外一个关键点是凸函数，能够找到全局最低点，就是你要知道什么时候停下来最合适。

回忆一下均方误差函数:

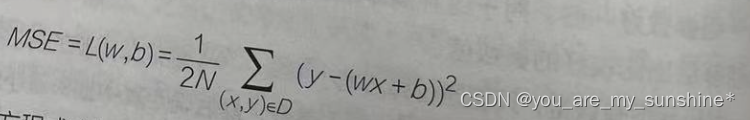
函数方程式中的x，y都可以视为常量，则L就只随着w和b 而变，而函数是连续的平滑曲线，每一个微小的w和b的改变都会带来微小的L的改变，而且这个函数很显然是个二次函数(w和b被平方)。为了简化描述，方便绘图，先忽略参数b。对于给定的数据集来说，平均损失L和w的对应关系如下图所示。

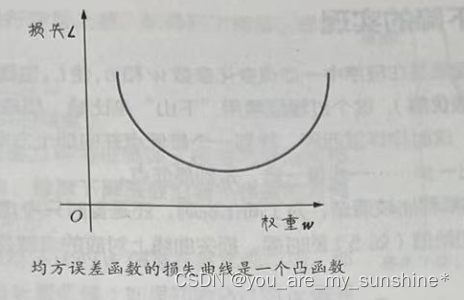
我们将这个函数图像称为损失曲线，这是一个凸函数。凸函数的图像会流畅、连续地形成相对于y轴的全局最低点，也就是说存在着全局最小损失点。这也是此处选择MSE作为线性回归的损失函数的原因。

梯度下降的实现

梯度下降的过程就是在程序中一点点变化参数w和b,使L也就是损失值,逐渐趋近最低点（也称为机器学习中的最优解）。这个过程经常用“下山”来比喻:想象你站在一座山的山腰上，正在寻找一条下山的路，这时你环望四周，找到一个最低点并向那个方向迈出一步;接着再环望四周朝最低点方向再迈出一步……一步接一步，走到最低点。
这里用图来详细解释比较清楚，为了简化说明，还是暂时只考虑权重w和损失L之间的关系、 给w随机分配一个初始值(如5)的时候，损失曲线上对应的点就是下图中有小猴子的地方。

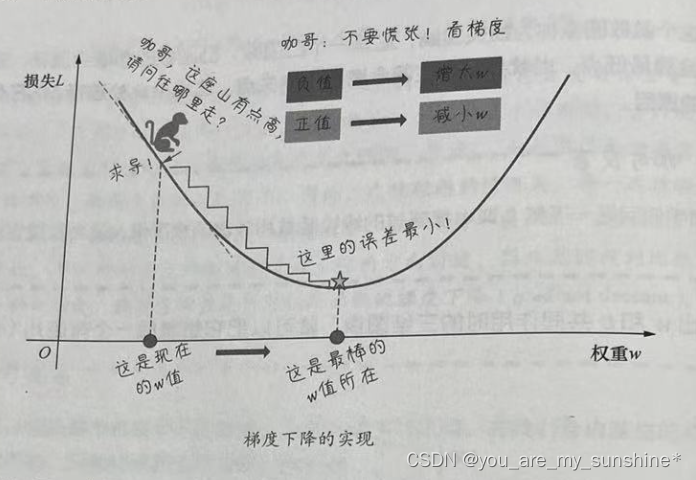
此时w等于5，下一步要进行新的猜测了，w应该往哪个方向移动，才能得到更小的损失L?也就是说，w应该是增大(5.01)还是减小(4.99)，L才能更快地趋近最小损失点(五角星)?
秘密武器正是导数。导数描述了函数在某点附近的变化率(L正在随着w增大而增大还是减小),而这正是进一步猜测更好的权重时所需要的全部内容。
程序中用梯度下降法通过求导来计算损失曲线在起点处的梯度。此时，梯度就是损失曲线导数的矢量，它可以让我们了解哪个方向距离目标“更近”或“更远”。

• 如果求导后梯度为正值,则说明L正在随着w增大而增大,应该减小w,以得到更小的损失。
• 如果求导后梯度为负值,则说明L正在随着w增大而减小,应该增大w,以得到更小的损失。

此处在单个权重参数的情况下，损失相对于权重的梯度就称为导数;若考虑偏置，或存在多1个权重参数时，损失相对于单个权重的梯度就称为偏导数。

因此，通过对损失曲线进行求导之后，就得到了梯度。梯度具有以下两个特征。

• 方向(也就是梯度的正负)。
• 大小(也就是切线倾斜的幅度)。
  这两个重要的特征，尤其是方向特征确保了梯度始终指向损失函数中增长最为迅猛的方向。梯度下降法会沿着负梯度的方向走一步，以降低损失。
  
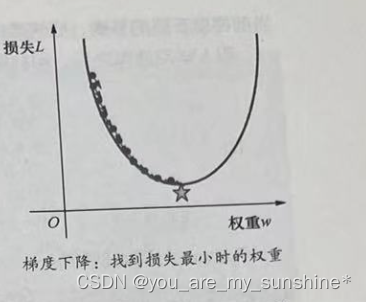
  通过梯度下降法，如果初始估计的w值落在最优值左边，那么梯度下降会将w增大，以趋近最低值;如果初始估计的w值落在最优值右边，那么梯度下降会将w减小，以趋近最低值。这个逐渐趋近于最优值的过程也叫作损失函数的收敛。

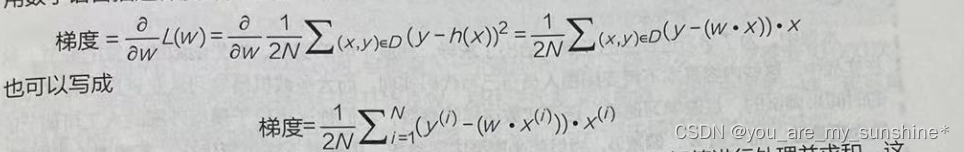
此处的N是数据集的数目。符号Σ代表对所有训练数据集中的特征和标签进行处理并求和，这是已经推导出来的求梯度的具体步骤。如果不熟悉导数(也就是对损失函数的微分)的演算也没有什么影响。因为梯度的计算过程都已经封装在各种机器学习框架中，并不用我们自己写代码实现。
而且即使要通过Python来实现梯度下降公式，代码同样是非常的简洁:

y_hat weight*x + bias这是向量化运算实现的假设函数
loss =y_hat-y#这是中间过程，求得的是假设函数预测的y'和真正的y值之间的差值 
derivative_wight - X.T.dot(loss)/len(X)#对权重求导，len(X)就是样本总数 
derivative_bias - sum(loss)*1/len (X)对偏置求导，len(X)就是样本总数

简单地解释一下这段代码。

• weight*X 是求出X数据集中的全部数据的y’值，就是w·x(i)的实现，是对数组的整体操作，不用通过循环去分别操作每一个数据。
• 对weight 求导的过程中，使用了上一课中介绍过的多项式点积规则一-两个相同维度的向量对应元素先相乘，后相加。这其中的两个向量是X和loss，也就是y(i)-( w·x(i))·x(i)的实现。
• 对偏置b求导并不需要与特征X相乘，因为偏置与权重不同，它与特征并不相关。另外还有一种思路，是把偏置看作W，那么就需要给X特征矩阵添加一行数字1,形成x0，与偏置相乘，同时确保偏置值不变——我们会在多变量线性回归的代码中试一下这个技巧。

学习速率也很重要

下一个问题是应该以多快的速度下山。这在机器学习中被称为学习速率(learing rate)的确定。学习速率也记作a，读作alpha。
学习速率乘以损失曲线求导之后的微分值，就是一次梯度变化的步长(step size )。它控制着当前梯度下降的节奏，或快或慢，w将在每一次迭代过程中被更新、优化。
引入学习速率之后，用数学语言描述参数w随梯度更新的公式如下:

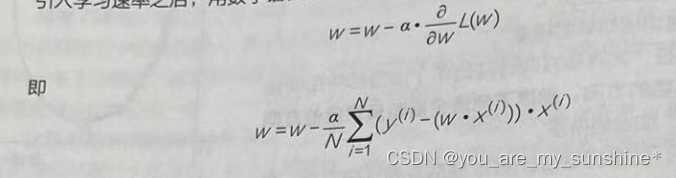
Python 代码实现如下:

weight = weight - alpha*derivative_wight#结合学习速率alpha更新权重
bias = bias - alpha*derivative_bias #结合学习速率alpha更新偏置 

大多数机器学习从业者真正花费相当的时间来调试的，是像学习速率、迭代次数这样的参数，我们称这类位于模型外部的人工可调节的参数为超参数。而权重w、偏置b，当然都是模型内部参数，由梯度下降负责优化，不需要人工调整。

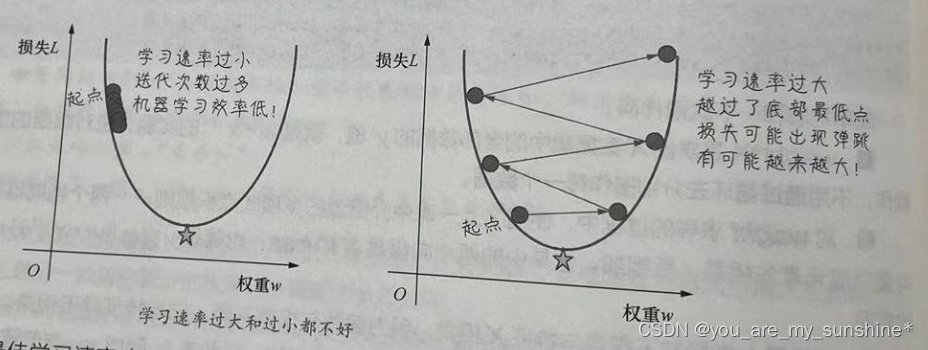
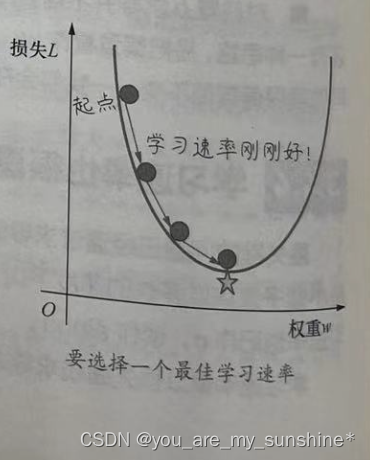
如果所选择的学习速率过小，机器就会花费很长的学习时间，需要迭代很多次才能到达损失函数的最底点，如下面左图所示。相反，如果学习速率过大，导致L的变化过大，越过了损失曲线的最低点，则下一个点将永远在U形曲线的底部随意弹跳，损失可能越来越大。

在机器学习实战中，这种损失不仅不会随着迭代次数减小，反而会越来越大的情况时有发生。

最佳学习速率(如图所示)与具体问题相关。因为在不同问题中，损失函数的平坦程度不同。如果我们知道损失函数的梯度较小，则可以放心地试着采用更大的学习速率，以补偿较小的梯度并获得更大的步长。
寻找最佳学习速率很考验经验和感觉。一个常见的策略是，在机器学习刚刚开始的时候，学习速率可以设置得大一些，快速几步达到靠近最佳权重的位置，当逐渐地接近最佳权重时，可以减小学习速率，防止一下子越过最优值。

---

学习机器学习的参考资料：
（1）书籍
利用Python进行数据分析
西瓜书
百面机器学习
机器学习实战
阿里云天池大赛赛题解析(机器学习篇)
白话机器学习中的数学
零基础学机器学习
图解机器学习算法
…

（2）机构
光环大数据
开课吧
极客时间
七月在线
深度之眼
贪心学院
拉勾教育
博学谷
…