Bit Extraction and Bootstrapping for BGV/BFV
参考文献:
- [GHS12] Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1-16.
- [AP13] Alperin-Sheriff J, Peikert C. Practical bootstrapping in quasilinear time[C]//Annual Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 1-20.
- [HS15] Halevi S, Shoup V. Bootstrapping for helib[J]. Journal of Cryptology, 2021, 34(1): 7.
- [CH18] Chen H, Han K. Homomorphic lower digits removal and improved FHE bootstrapping[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Cham: Springer International Publishing, 2018: 315-337.
- [GV23] Geelen R, Vercauteren F. Bootstrapping for BGV and BFV Revisited[J]. Journal of Cryptology, 2023, 36(2): 12.
文章目录
GHS12
多项式环 R : = Z [ X ] / ( F ( X ) ) R:=\mathbb Z[X]/(F(X)) R:=Z[X]/(F(X)),明文空间 p = 2 p=2 p=2,密文模数 gcd ? ( q , p ) = 1 \gcd(q,p)=1 gcd(q,p)=1,BGV 方案的解密分为三步:
- 计算私钥上的依赖密文的线性函数, Z = ? c , s ? ? m o d ? F Z=\langle c,s\rangle \bmod F Z=?c,s?modF
- 模掉密文模数, e = [ Z ] q e = [Z]_q e=[Z]q?,这里 e = 2 u + μ ∈ R e=2u+\mu \in R e=2u+μ∈R
- 提取最低比特位, μ = [ e ] 2 \mu = [e]_2 μ=[e]2?
[GHS12] 的一个重要观察是:如果 q = 2 r + 1 q=2^r+1 q=2r+1,那么解密过程可以简化。我们用 z [ i ] z[i] z[i] 表示整系数 z z z 的第 i i i 个比特(索引从 0 0 0 开始),用 z [ j : i ] z[j:i] z[j:i] 表示截取部分比特。
-
假如 Z Z Z 某个系数 z z z 的规模远小于 q 2 q^2 q2 量级(这是合理的,因为 c c c 的系数规模仅为 q q q 量级),那么必定有
[ [ z ] q ] 2 = [ z [ r ? 1 : 0 ] ? z [ 2 r ? 1 : r ] ] 2 = [ z [ 0 ] ? z [ r ] ] 2 = z [ r ] ⊕ z [ 0 ] \begin{aligned} \big[[z]_q\big]_2 &= \big[z[r-1:0] - z[2r-1:r]\big]_2\\ &= \big[z[0] - z[r]\big]_2\\ &= z[r] \oplus z[0] \end{aligned} [[z]q?]2??=[z[r?1:0]?z[2r?1:r]]2?=[z[0]?z[r]]2?=z[r]⊕z[0]? -
(仅在自举时)采用新的明文空间 p ′ = 2 r + 1 p'=2^{r+1} p′=2r+1,我们将私钥 s s s 作为空间 R p ′ R_{p'} Rp′? 中的明文,加密为 BK 公开
-
同态计算出 Z ( m o d p ′ ) Z \pmod{p'} Z(modp′),它的各个系数恰为 z [ r : 0 ] z[r:0] z[r:0],我们只需再同态提取出 z [ r ] z[r] z[r] 和 z [ 0 ] z[0] z[0] 即可
现在的问题就是,如何同态提取出 R p ′ R_{p'} Rp′? 的 MSB 和 LSB?
Extracting the Top and Bottom Bits
[GHS12] 的另一个重要观察是:因为
p
′
p'
p′ 是二的幂次,从而有
[
z
2
]
p
′
=
[
(
z
[
r
:
1
]
?
2
k
+
z
[
0
]
)
2
]
p
′
=
[
z
[
r
:
1
]
2
?
2
2
k
+
z
[
r
:
1
]
?
z
[
0
]
?
2
k
+
1
+
z
[
0
]
]
p
′
=
[
z
[
r
:
1
]
2
?
2
k
?
1
+
z
[
r
:
1
]
?
z
[
0
]
]
p
′
/
2
k
+
1
?
2
k
+
1
+
z
[
0
]
\begin{aligned} \big[z^2\big]_{p'} &= \big[(z[r:1] \cdot 2^{k} + z[0])^2\big]_{p'}\\ &= \big[z[r:1]^2 \cdot 2^{2k} + z[r:1] \cdot z[0] \cdot 2^{k+1} + z[0]\big]_{p'}\\ &= \big[z[r:1]^2 \cdot 2^{k-1} + z[r:1] \cdot z[0]\big]_{p'/2^{k+1}} \cdot 2^{k+1} + z[0] \end{aligned}
[z2]p′??=[(z[r:1]?2k+z[0])2]p′?=[z[r:1]2?22k+z[r:1]?z[0]?2k+1+z[0]]p′?=[z[r:1]2?2k?1+z[r:1]?z[0]]p′/2k+1??2k+1+z[0]?
它保持 LSB 不变,在 LSB 的高位不断插入零。
因此,对于任意的整数
z
=
∑
i
=
0
r
2
i
z
[
i
]
z=\sum_{i=0}^r 2^i z[i]
z=∑i=0r?2iz[i],初始化
w
0
:
=
z
w_0:=z
w0?:=z,计算出
w
i
:
=
z
?
∑
j
=
0
i
?
1
2
j
w
j
2
i
?
j
(
m
o
d
2
r
+
1
)
2
i
w_i := \frac{z-\sum_{j=0}^{i-1}2^jw_j^{2^{i-j}} \pmod{2^{r+1}}}{2^i}
wi?:=2iz?∑j=0i?1?2jwj2i?j?(mod2r+1)?
那么就有
w
i
[
0
]
=
z
[
i
]
,
?
i
w_i[0] = z[i],\forall i
wi?[0]=z[i],?i,这便提取出了 MSB 和 LSB。其中的除法
a
/
2
i
a/2^i
a/2i 是整除的,因此可以直接计算
c
t
?
[
2
?
i
]
q
ct \cdot [2^{-i}]_{q}
ct?[2?i]q? 即可。副作用是噪声
p
′
u
p'u
p′u 也缩放为了
p
′
2
?
i
u
=
2
r
?
i
+
1
u
p'2^{-i}u = 2^{r-i+1}u
p′2?iu=2r?i+1u(侵蚀明文空间高位),因此输出的是
w
i
∈
Z
2
r
?
i
+
1
w_i \in \mathbb Z_{2^{r-i+1}}
wi?∈Z2r?i+1?,特别地
w
0
∈
Z
2
r
+
1
w_0 \in \mathbb Z_{2^{r+1}}
w0?∈Z2r+1? 以及
w
r
=
Z
2
w_r = \mathbb Z_{2}
wr?=Z2?。当然,这并不影响两者的加和,
w
r
+
w
0
≡
z
[
r
]
⊕
z
[
0
]
∈
Z
2
w_r+w_0 \equiv z[r] \oplus z[0] \in \mathbb Z_2
wr?+w0?≡z[r]⊕z[0]∈Z2?
算法如图所示:

Lower-Degree Bit Extraction
由于自举需要的明文模数 p ′ = 2 r + 1 p'=2^{r+1} p′=2r+1 其规模依赖于密文模数 q = 2 r + 1 q=2^r+1 q=2r+1,参数 r r r 越小,则比特提取程序的计算速度和乘法深度都可以降低。[GHS12] 给出了优化技术:在密文 ( c 0 , c 1 ) ( m o d q ) (c_0,c_1) \pmod q (c0?,c1?)(modq) 上添加一些 q q q 的倍数,使得它们的系数都整除 2 r ′ , 1 ≤ r ′ < r 2^{r'},1\le r'<r 2r′,1≤r′<r,记为 ( c 0 ′ , c 1 ′ ) (c_0',c_1') (c0′?,c1′?),易知它加密相同的消息。
只要 c t ′ ct' ct′ 的系数依旧远小于 q 2 q^2 q2 规模,令 Z ′ = c 0 ′ + c 1 ′ ? s Z'=c_0'+c_1' \cdot s Z′=c0′?+c1′??s,易知也有 2 r ′ ∣ Z ′ 2^{r'}|Z' 2r′∣Z′,因此 z ′ [ 0 ] = 0 z'[0]=0 z′[0]=0,从而有 μ = z ′ [ r ] \mu = z'[r] μ=z′[r]。进一步的,我们将 ( c 0 ′ , c 1 ′ ) (c_0',c_1') (c0′?,c1′?) 整除(等价于求逆)掉 2 r ′ 2^{r'} 2r′ 成为 ( c 0 ′ ′ , c 1 ′ ′ ) (c_0'',c_1'') (c0′′?,c1′′?),那么就有 μ = z ′ ′ [ r ? r ′ ] \mu = z''[r-r'] μ=z′′[r?r′],现在只需要明文模数 p ′ = 2 r ? r ′ + 1 p'=2^{r-r'+1} p′=2r?r′+1 即可。
Bootstrapping with Packed Ciphertexts
由于自举时采用明文空间
R
p
′
R_{p'}
Rp′?,其中
p
′
=
2
r
+
1
p'=2^{r+1}
p′=2r+1 是二的幂次(而非素数),因此 SIMD 技术存在一些改变。任意素数
p
p
p(包括
p
=
2
p=2
p=2),[GHS12] 将空间
Z
/
p
t
Z
\mathbb Z/p^t\mathbb Z
Z/ptZ 视为
p
p
p-adic integers 的精度
t
t
t 近似(局部域——p-进数),定义符号
Z
p
:
=
{
∑
i
=
0
∞
a
i
?
p
i
∣
a
i
∈
F
p
}
\mathbb Z_p := \left\{ \sum_{i=0}^\infty a_i \cdot p^i \Big| a_i \in \mathbb F_p \right\}
Zp?:={i=0∑∞?ai??pi
?ai?∈Fp?}
它是
p
p
p 上的形式幂级数,表示全部的
p
p
p-adic integers。当
t
t
t 趋于无穷,
Z
/
p
t
Z
\mathbb Z/p^t\mathbb Z
Z/ptZ 的极限就是
Z
p
\mathbb Z_p
Zp?,因此
R
p
t
R_{p^t}
Rpt? 是
R
p
∞
R_{p^\infty}
Rp∞? 的精度
t
t
t 近似。
Hensel Lifting:素数 p p p,整数 t ≥ 1 t \ge 1 t≥1,假设 G , H , F ∈ Z [ X ] G,H,F \in \mathbb Z[X] G,H,F∈Z[X] 是首一多项式,并且满足
- 在模数 p p p 下, G , H G,H G,H 互素
- G ? H = F ( m o d p t ) G \cdot H = F \pmod{p^t} G?H=F(modpt)
那么存在首一多项式 G ˉ , H ˉ ∈ Z [ X ] \bar G,\bar H \in \mathbb Z[X] Gˉ,Hˉ∈Z[X],使得
- G ˉ ≡ G ( m o d p t ) \bar G \equiv G \pmod{p^t} Gˉ≡G(modpt) 以及 H ˉ ≡ H ( m o d p t ) \bar H \equiv H \pmod{p^t} Hˉ≡H(modpt)
- G ˉ ? H ˉ = F ( m o d p t + 1 ) \bar G \cdot \bar H = F \pmod{p^{t+1}} Gˉ?Hˉ=F(modpt+1)
这个定理可以用于将 p p p 下的解,提升到任意的 p t p^t pt 下的解(具体怎么构造的?论文没写):
- 模 p p p 平方自由的多项式 F F F,它在模 p t p^t pt 下不可约,当仅当它在模 p p p 下不可约
- 模 p p p 平方自由的多项式 F F F,它在模 p t p^t pt 下的分解,由它在模 p p p 下的分解唯一确定
这意味这,任意的 t ≥ 1 t \ge 1 t≥1, F ( X ) ( m o d p t ) F(X) \pmod{p^t} F(X)(modpt) 的明文槽,与 F ( X ) ( m o d p ) F(X) \pmod{p} F(X)(modp) 的基本相同。
给定分圆多项式
Φ
m
(
X
)
\Phi_m(X)
Φm?(X),假设
p
(
m
o
d
m
)
p \pmod m
p(modm) 的乘法阶是
d
d
d,那么它在模
p
p
p 下可以分解为
l
=
?
(
m
)
/
d
l=\phi(m)/d
l=?(m)/d 个不同的首一不可约因子,
Φ
m
(
X
)
=
∏
j
=
0
l
=
1
F
j
(
X
)
(
m
o
d
p
)
\Phi_m(X) = \prod_{j=0}^{l=1} F_j(X) \pmod{p}
Φm?(X)=j=0∏l=1?Fj?(X)(modp)
然后利用 Hensel Lifting 定理,可以获得提升后的分解:
Φ
m
(
X
)
=
∏
j
=
0
l
=
1
F
ˉ
j
(
X
)
(
m
o
d
p
t
)
\Phi_m(X) = \prod_{j=0}^{l=1} \bar F_j(X) \pmod{p^t}
Φm?(X)=j=0∏l=1?Fˉj?(X)(modpt)
其中
F
ˉ
j
≡
F
j
(
m
o
d
p
)
\bar F_j \equiv F_j \pmod{p}
Fˉj?≡Fj?(modp) 是模
p
t
p^t
pt 下首一不可约多项式。根据 CRT,明文槽的结构为:
(
Z
/
p
t
Z
)
[
X
]
/
(
F
ˉ
j
(
X
)
)
?
(
Z
/
p
t
Z
)
[
X
]
/
(
G
(
X
)
)
,
?
j
=
0
,
?
?
,
l
?
1
(\mathbb Z/p^t\mathbb Z)[X]/(\bar F_j(X)) \cong (\mathbb Z/p^t\mathbb Z)[X]/(G(X)), \forall j=0,\cdots,l-1
(Z/ptZ)[X]/(Fˉj?(X))?(Z/ptZ)[X]/(G(X)),?j=0,?,l?1
其中
G
(
X
)
G(X)
G(X) 是任意的
F
p
\mathbb F_p
Fp? 下
d
d
d 次不可约多项式,可以简单地取为
F
ˉ
0
(
X
)
\bar F_0(X)
Fˉ0?(X)。简记
R
p
t
,
d
R_{p^t,d}
Rpt,d? 是这个明文槽代数结构,它包含了
d
d
d 次本原单位根。
G
a
l
(
R
p
t
)
?
(
Z
/
m
Z
)
?
\mathcal{Gal}(R_{p^t}) \cong (\mathbb Z/m\mathbb Z)^*
Gal(Rpt?)?(Z/mZ)?,所有自同构形如
X
?
X
i
X \mapsto X^i
X?Xi,
- 由 p p p 生成的 d d d 阶(乘法)循环群,它们是 Frobenius maps,独立地作用在各个槽上
- 商群 ( Z / m Z ) ? / ( p ) (\mathbb Z/m\mathbb Z)^*/(p) (Z/mZ)?/(p) 的阶 l = ? ( m ) / d l=\phi(m)/d l=?(m)/d,它们组成了集合 [ l ] [l] [l] 上的 sharply transitive permutations,可用于实现明文槽直接的任意置换(Benes Network)
利用这些自同构,可以实现批处理的比特提取(相位的每个系数)。自举基本框架:
- 同态计算线性函数,获得 Z ( X ) ∈ R 2 r + 1 Z(X) \in R_{2^{r+1}} Z(X)∈R2r+1?
- 同态计算 Inv-DFT,将 Z ( X ) Z(X) Z(X) 的各个系数转换到明文槽。实际上系数 z ∈ Z 2 r + 1 z \in \mathbb Z_{2^{r+1}} z∈Z2r+1? 仅存放在 R 2 r + 1 , d R_{2^{r+1},d} R2r+1,d? 的基环上(每个密文仅包含 l l l 个槽,共需要 d d d 个密文)
- 同态计算比特提取程序,计算出 z [ r ] ⊕ z [ 0 ] ∈ Z 2 z[r] \oplus z[0] \in \mathbb Z_2 z[r]⊕z[0]∈Z2?,它放在了 R 2 , d R_{2,d} R2,d? 的基环上
- 同态计算 DFT,将明文槽中的 μ i \mu_i μi? 打包为多项式 μ ( X ) ∈ R 2 \mu(X) \in R_2 μ(X)∈R2?
AP13
[AP13] 采用了 [GHS12] 的简单解密方法,但是没有使用 Benes Network 去执行线性变换,而是利用了 Ring/Feild-Switching 技术,利用 Trace 在分圆塔上移动,实现线性变换的张量分解(tensor decomposition)。然而 [HS15] 指出:由于自举结果只有较少的 Level,因此张量分解也只能是粗粒度的,从而不消耗过多的 Level;同时为了安全性,因为噪声是超多项式的小,切换后的 Ring 应当维度很大;并且使用 [HS18] 的 BSGS 矩阵向量算法后,自举开销主要是比特提取,继续优化线性变换的意义不大。
HS15
[HS15] 最早发在 2015 美密上,之后整合了 [HS18] 的线性变换技术以及 [CH18] 的 “薄” 自举技术,还有一些其他的小优化,重新发表在 2021 密码学杂志上。
[HS15] 将 [GHS12] 的自举技术从只能处理特征 p = 2 p=2 p=2,给推广到可以处理任意的素数特征。首先我们确定整数 z z z 的 base- p p p representation,
-
p = 2 p=2 p=2 时,符号 [ z ] 2 [z]_2 [z]2? 取值范围 { 0 , 1 } \{0,1\} {0,1},二补数表示(2’s-complement representation of signed integers)
z [ j : i ] = ∑ k = i j ? 1 2 k ? i z [ k ] ? 2 j ? i z [ j ] z[j:i] = \sum_{k=i}^{j-1}2^{k-i}z[k] - 2^{j-i}z[j] z[j:i]=k=i∑j?1?2k?iz[k]?2j?iz[j]
其中 z [ k ] ∈ { 0 , 1 } z[k] \in \{0,1\} z[k]∈{0,1},换句话说 MSB 表示了一个很大的负数 -
p > 2 p>2 p>2 时,符号 [ z ] p [z]_p [z]p? 取值范围 [ ? ( p ? 1 ) / 2 , ( p ? 1 ) / 2 ] [-(p-1)/2,(p-1)/2] [?(p?1)/2,(p?1)/2],平衡 p p p 进制表示( balanced base-p representation of signed integers)
z [ j : i ] = ∑ k = i j p k ? i z [ k ] z[j:i] = \sum_{k=i}^{j}p^{k-i}z[k] z[j:i]=k=i∑j?pk?iz[k]
其中 z [ k ] ∈ [ ? ( p ? 1 ) / 2 , ( p ? 1 ) / 2 ] z[k] \in [-(p-1)/2,(p-1)/2] z[k]∈[?(p?1)/2,(p?1)/2]
Hypercube structure
在 HElib 实现中的本地明文空间是
R
p
r
R_{p^r}
Rpr?,其中
p
p
p 是素数,
r
r
r 是 Hensel Lifting 参数。密文模数
q
q
q,私钥
s
∈
R
s \in R
s∈R,密文
(
c
0
,
c
1
)
∈
R
q
(c_0,c_1) \in R_q
(c0?,c1?)∈Rq?,那么有
[
c
0
+
c
1
?
s
]
q
=
m
+
p
r
e
∈
R
[c_0+c_1 \cdot s]_q = m+p^re \in R
[c0?+c1??s]q?=m+pre∈R,其中
e
∈
R
e \in R
e∈R 是短噪声,
m
∈
R
p
r
m \in R_{p^r}
m∈Rpr? 是明文。
利用 Hensel Lifting 以及 CRT,分解出
Φ
m
(
X
)
=
∏
i
=
1
k
F
i
(
X
)
(
m
o
d
p
r
)
\Phi_m(X) = \prod_{i=1}^k F_i(X) \pmod{p^r}
Φm?(X)=∏i=1k?Fi?(X)(modpr),每个因子
F
i
F_i
Fi? 的度数都是
p
(
m
o
d
m
)
p \pmod m
p(modm) 的乘法阶
d
d
d,个数为
k
=
?
(
m
)
/
d
k=\phi(m)/d
k=?(m)/d,同构为
R
p
r
?
?
i
=
1
k
Z
[
X
]
/
(
p
r
,
F
i
(
X
)
)
R_{p^r} \cong \bigoplus_{i=1}^k \mathbb Z[X]/(p^r,F_i(X))
Rpr??i=1?k?Z[X]/(pr,Fi?(X))
我们定义
E
:
=
Z
[
X
]
/
(
p
r
,
F
1
(
X
)
)
E := \mathbb Z[X]/(p^r,F_1(X))
E:=Z[X]/(pr,F1?(X)) 是明文槽的代数结构,令
ζ
\zeta
ζ 是
m
m
m-th 本原单位根
X
X
X 在
E
E
E 中所在的剩余类,于是有
E
=
Z
p
r
[
ζ
]
E = \mathbb Z_{p^r}[\zeta]
E=Zpr?[ζ]
假设
S
?
Z
S \subseteq \mathbb Z
S?Z 是商群
Z
m
?
/
(
p
)
\mathbb Z_m^*/(p)
Zm??/(p) 的完全代表(complete system of representatives),
∣
S
∣
=
k
|S|=k
∣S∣=k,那么就有如下的同构映射,
R
p
r
→
?
h
∈
S
E
α
?
{
α
(
ζ
h
)
}
h
∈
S
\begin{aligned} R_{p_r} &\to \bigoplus_{h \in S} E\\ \alpha &\mapsto \{\alpha(\zeta^h)\}_{h \in S} \end{aligned}
Rpr??α?→h∈S??E?{α(ζh)}h∈S??
自同构映射
τ
j
:
α
(
X
)
?
α
(
X
j
)
,
?
j
∈
Z
m
?
\tau_j: \alpha(X) \mapsto \alpha(X^j), \forall j \in \mathbb Z_m^*
τj?:α(X)?α(Xj),?j∈Zm??,它们诱导了明文槽的超立方结构:HElib 记录了超立方基(hypercube basis )
g
1
,
?
?
,
g
n
∈
Z
m
?
g_1,\cdots,g_n \in \mathbb Z_m^*
g1?,?,gn?∈Zm??,以及它们的阶
l
1
,
?
?
,
l
n
l_1,\cdots,l_n
l1?,?,ln?(并非是
Z
m
?
\mathbb Z_m^*
Zm?? 中的乘法阶),使得
Z
m
?
/
(
p
)
\mathbb Z_m^*/(p)
Zm??/(p) 的代表为
S
:
=
{
g
1
e
1
?
g
n
e
n
∣
0
≤
e
i
<
l
i
}
S := \{g_1^{e_1} \cdots g_n^{e_n} | 0 \le e_i < l_i\}
S:={g1e1???gnen??∣0≤ei?<li?}
那么,每个元素
h
h
h(明文槽)都对应一个索引
(
e
1
,
?
?
,
e
n
)
(e_1,\cdots,e_n)
(e1?,?,en?),我们将 “固定其他坐标遍历
e
i
e_i
ei? 坐标的那些槽” 称为维度
i
i
i 上的超列(hypercolumn)。我们将超列中的每个槽
(
?
?
,
e
i
,
?
?
)
(\cdots,e_i,\cdots)
(?,ei?,?) 映射到
(
?
?
,
e
i
+
v
(
m
o
d
l
i
)
,
?
?
)
(\cdots,e_i+v \pmod{l_i},\cdots)
(?,ei?+v(modli?),?) 称为维度
i
i
i 上的旋转。具体的实现为:
- 假如 g i g_i gi? 在 Z m ? \mathbb Z_m^* Zm?? 上的乘法阶恰为 l i l_i li?,那么定义 ρ i v ( α ) : = τ g i v ( α ) \rho_i^v(\alpha) := \tau_{g_i^v}(\alpha) ρiv?(α):=τgiv??(α),我们称 i i i 是 “good dimension”(只需一次自同构)
- 假如 g i g_i gi? 在 Z m ? \mathbb Z_m^* Zm?? 上的乘法阶不是 l i l_i li?,那么定义 ρ i v ( α ) : = τ g i v ( mask ? α ) + τ g i v ? l i ( ( 1 ? mask ) ? α ) \rho_i^v(\alpha) := \tau_{g_i^v}(\text{mask} \cdot \alpha) + \tau_{g_i^{v-l_i}}((1-\text{mask}) \cdot \alpha) ρiv?(α):=τgiv??(mask?α)+τgiv?li???((1?mask)?α),我们称 i i i 是 “bad dimension”(需要两次自同构)
除了这些 rotate1D 自同构,循环群
(
p
)
(p)
(p) 对应的那些自同构是 Frobenius map,可用于计算明文槽本身的线性变换。假设
M
M
M 是明文槽
E
E
E 上的
Z
p
r
\mathbb Z_{p^r}
Zpr?-线性变换(注意区分各个槽之间的
E
E
E-线性变换),那么总存在唯一的常数集
θ
0
,
?
?
,
θ
d
?
1
\theta_0,\cdots,\theta_{d-1}
θ0?,?,θd?1?,使得
M
M
M 写为如下的线性化多项式(linearized polynomials),
M
(
a
)
=
∑
i
=
0
d
?
1
θ
i
τ
p
i
(
a
)
,
?
a
∈
E
M(a) = \sum_{i=0}^{d-1} \theta_i \tau_p^i(a), \forall a \in E
M(a)=i=0∑d?1?θi?τpi?(a),?a∈E
给定
M
M
M 的描述(比如 power basis 的像),可以通过求解模
p
p
p 下的线性方程组,获得 mod-
p
p
p solutions,然后利用 Hensel Lifting 提升到模
p
r
p^r
pr 下即可获得
θ
i
\theta_i
θi? 的具体值。对于不同的明文槽,可以执行不同的变换
M
M
M;我们计算出它们的常数后,打包为
d
d
d 个多项式,用于同态计算明文槽内部的线性变换。
Recryption Procedure
[HS15] 采取了 [GHS12] 的自举框架:明文模数 p r p^r pr,密文模数 q = p e + 1 q=p^e+1 q=pe+1,自举需要的明文模数为 p e + r p^{e+r} pe+r,那么
- 首先计算 u = [ ? s k , c t ? ] p e + r u = [\langle sk,ct \rangle]_{p^{e+r}} u=[?sk,ct?]pe+r?
- 然后计算 m = u [ r ? 1 : 0 ] ? u [ e + r ? 1 : e ] ( m o d p r ) m = u[r-1:0] - u[e+r-1:e] \pmod{p^r} m=u[r?1:0]?u[e+r?1:e](modpr)
为了降低乘法深度,可以设置中等规模参数 r ≤ e ′ < e r \le e' <e r≤e′<e,使得密文 c t ′ ct' ct′ 可被 p e ′ p^{e'} pe′ 整除,从而我们计算 u ′ = [ ? s k , c t ′ / p e ′ ? ] p e + r u' = [\langle sk,ct'/p^{e'} \rangle]_{p^{e+r}} u′=[?sk,ct′/pe′?]pe+r?,然后输出 m = ? u ′ [ e ? e ′ + r ? 1 : e ? e ′ ] ( m o d p r ) m = -u'[e-e'+r-1:e-e'] \pmod{p^r} m=?u′[e?e′+r?1:e?e′](modpr)
[GHS12] 的 ”通过平方插入零“ 的技巧仅适用于 p = 2 p=2 p=2 的情况,[HS15] 给出了更一般的 Lifting Polynomials,适用于任意的 p r p^r pr 情况。由于 [HS15] 采取了带符号的二补数和平衡进制表示,因此解密公式略有不同。
Simpler Decryption Formula:对于任意的素数 p > 1 p>1 p>1,整数 e > r ≥ 1 , ?? q = p e + 1 e>r\ge1,\,\, q=p^e+1 e>r≥1,q=pe+1,假设 z z z 是满足 z / q z/q z/q 和 [ z ] q [z]_q [z]q? 规模都远小于 q q q 的整数,具体来说, ∣ z / q ∣ + ∣ [ z ] q ∣ ≤ ( q ? 1 ) / 2 |z/q|+|[z]_q| \le (q-1)/2 ∣z/q∣+∣[z]q?∣≤(q?1)/2,那么
- 当 p = 2 p=2 p=2 时, [ z ] q = z [ r ? 1 : 0 ] ? z [ e + r ? 1 : e ] ? z [ e ? 1 ] ( m o d 2 r ) [z]_q = z[r-1:0] - z[e+r-1:e] - z[e-1] \pmod{2^r} [z]q?=z[r?1:0]?z[e+r?1:e]?z[e?1](mod2r)
- 当 p > 2 p>2 p>2 时, [ z ] q = z [ r ? 1 : 0 ] ? z [ e + r ? 1 : e ] ( m o d p r ) [z]_q = z[r-1:0] - z[e+r-1:e] \pmod{p^r} [z]q?=z[r?1:0]?z[e+r?1:e](modpr)
Reduce the number of digits:对于任意的整数 e ′ ≥ 1 e'\ge 1 e′≥1 以及 q > p > 1 q>p>1 q>p>1,使得 q ≡ 1 ( m o d p e ′ ) q \equiv 1 \pmod{p^{e'}} q≡1(modpe′),任给整数 z z z 总存在 ∣ v ∣ ≤ p e ′ / 2 |v| \le p^{e'}/2 ∣v∣≤pe′/2,它使得 z + v ? q ≡ 0 ( m o d p e ′ ) z+v\cdot q \equiv 0 \pmod{p^{e'}} z+v?q≡0(modpe′)
The digit-extraction procedure:对于任意的素数 p p p 和指数 e ≥ 1 e \ge 1 e≥1,任意的形如 z = z 0 + p e z 1 , ?? z 0 ∈ [ p ] , z 1 ∈ Z z=z_0+p^ez_1,\,\, z_0 \in [p], z_1 \in \mathbb Z z=z0?+pez1?,z0?∈[p],z1?∈Z 的整数,满足 z p = z 0 ( m o d p ) z^p=z_0 \pmod{p} zp=z0?(modp) 以及 z p = z 0 p ( m o d p e + 1 ) z^p = z_0^p \pmod{p^{e+1}} zp=z0p?(modpe+1)
由于
z
p
(
m
o
d
p
e
+
1
)
z^p \pmod{p^{e+1}}
zp(modpe+1) 仅依赖于
z
0
=
[
z
]
p
e
∈
[
p
]
z_0=[z]_{p^e} \in [p]
z0?=[z]pe?∈[p] 的值,因此可以遍历
z
0
z_0
z0? 计算出
z
p
(
m
o
d
p
e
+
1
)
z^p \pmod{p^{e+1}}
zp(modpe+1) 的各个数位,然后采取拉格朗日插值公式(
f
i
(
z
0
)
=
z
p
[
i
]
f_i(z_0)=z^p[i]
fi?(z0?)=zp[i]),计算出
f
1
,
f
2
,
?
f_1,f_2,\cdots
f1?,f2?,? 序列(有限个非凡的,后续的都是
f
i
=
0
f_i=0
fi?=0),它们的度数至多为
p
?
1
p-1
p?1。对于任意的
e
≥
1
e \ge 1
e≥1 和整数
z
=
z
0
+
p
e
z
1
,
??
z
0
∈
[
p
]
,
z
1
∈
Z
z=z_0+p^ez_1,\,\, z_0 \in [p], z_1 \in \mathbb Z
z=z0?+pez1?,z0?∈[p],z1?∈Z,总满足
z
p
=
z
0
+
∑
i
=
1
e
f
i
(
z
0
)
p
i
(
m
o
d
p
e
+
1
)
z^p = z_0 + \sum_{i=1}^e f_i(z_0)p^i \pmod{p^{e+1}}
zp=z0?+i=1∑e?fi?(z0?)pi(modpe+1)
因此,对于任意的
e
≥
1
e \ge 1
e≥1,我们定义
deg
?
=
p
\deg=p
deg=p 的多项式:
F
e
(
X
)
=
X
p
?
∑
i
=
1
e
f
i
(
X
)
p
i
F_e(X) = X^p - \sum_{i=1}^e f_i(X)p^i
Fe?(X)=Xp?i=1∑e?fi?(X)pi
对于任意的
1
≤
e
′
≤
e
1 \le e' \le e
1≤e′≤e,任给形如
z
=
z
0
+
p
e
′
z
1
,
??
z
0
∈
[
p
]
,
z
1
∈
Z
z=z_0+p^{e'}z_1,\,\, z_0 \in [p], z_1 \in \mathbb Z
z=z0?+pe′z1?,z0?∈[p],z1?∈Z 的整数,都有
F
e
(
z
)
=
z
0
(
m
o
d
p
e
′
+
1
)
F_e(z) = z_0 \pmod{p^{e'+1}}
Fe?(z)=z0?(modpe′+1),这便实现了 “高位插入零” 的效果。通过
F
e
F_e
Fe? 的复合迭代,它可以将
z
0
+
p
z
1
z_0+pz_1
z0?+pz1? 映射为
z
0
(
m
o
d
p
e
+
1
)
z_0 \pmod{p^{e+1}}
z0?(modpe+1) ,从而实现 LSB 的提取。再将 LSB 不断移除,也可以实现 MSB 的提取。

特别地,对于 p = 2 , 3 p=2,3 p=2,3,恰好是 F e ( X ) = X p , ? e F_e(X)=X^p, \forall e Fe?(X)=Xp,?e,这便是 [GHS12] 所使用的平方技巧。
Linear Transformations
本地明文空间 Z p r [ X ] / ( Φ m ( X ) ) \mathbb Z_{p^r}[X]/(\Phi_m(X)) Zpr?[X]/(Φm?(X)),我们考虑 m m m 的分解 m 1 ? m t m_1\cdots m_t m1??mt?,它们两两互素(比如素数幂分解),那么 h ∈ Z m h \in \mathbb Z_m h∈Zm? 可以写作 h = CRT ( h 1 , ? ? , h t ) , h i ∈ [ m i ] h=\text{CRT}(h_1,\cdots,h_t), h_i \in [m_i] h=CRT(h1?,?,ht?),hi?∈[mi?]
商群 Z m ? / ( p ) \mathbb Z_{m}^*/(p) Zm??/(p) 的超立方结构:
- 我们令 p ( m o d m 1 ) p\pmod{m_1} p(modm1?) 的乘法阶是 d 1 d_1 d1?,对于 i ≥ 2 i\ge 2 i≥2 定义 d i d_i di? 是 p d 1 ? d i ? 1 ( m o d m i ) p^{d_1\cdots d_{i-1}} \pmod{m_i} pd1??di?1?(modmi?) 的乘法阶,那么 d : = d 1 ? d t d:=d_1\cdots d_t d:=d1??dt? 就是 d ( m o d m ) d \pmod{m} d(modm) 的乘法阶。
- 我们令 S i ? [ m i ] S_i \subseteq [m_i] Si??[mi?] 是商群 Z m i ? / ( p d 1 ? d i ? 1 ) \mathbb Z_{m_i}^*/(p^{d_1\cdots d_{i-1}}) Zmi???/(pd1??di?1?) 的完全代表,那么 S : = CRT ( S 1 , ? ? , S t ) S:=\text{CRT}(S_1,\cdots,S_t) S:=CRT(S1?,?,St?) 就是 Z m ? / ( p ) \mathbb Z_{m}^*/(p) Zm??/(p) 的完全代表。
现在我们需要将这里的 S : = CRT ( S 1 , ? ? , S t ) S:=\text{CRT}(S_1,\cdots,S_t) S:=CRT(S1?,?,St?) 和前两节的 S : = { g 1 e 1 ? g n e n ∣ 0 ≤ e i < l i } S := \{g_1^{e_1} \cdots g_n^{e_n} | 0 \le e_i < l_i\} S:={g1e1???gnen??∣0≤ei?<li?} 统一起来,这限制了 m m m 的选取:
- 限制
m
m
m 及其分解,使得
Z
m
i
?
/
(
p
d
1
?
d
i
?
1
)
\mathbb Z_{m_i}^*/(p^{d_1\cdots d_{i-1}})
Zmi???/(pd1??di?1?) 是循环群,
- 生成元 g ˉ i ∈ [ m i ] \bar g_i \in [m_i] gˉ?i?∈[mi?],乘法阶 k i k_i ki?
- 集合 S i : = { g ˉ i e i ∣ 0 ≤ e i < k i } S_i:=\{\bar g_i^{e_i}| 0\le e_i<k_i\} Si?:={gˉ?iei??∣0≤ei?<ki?}
- 定义 g i = CRT ( 1 , ? ? , g ˉ i , ? ? , 1 ) ∈ [ m ] g_i=\text{CRT}(1,\cdots,\bar g_i,\cdots,1) \in [m] gi?=CRT(1,?,gˉ?i?,?,1)∈[m] 是超立方基,那么 S S S 的那两种定义是同一个
- 限制
m
m
m 及其分解,使得
d
1
=
d
d_1=d
d1?=d 和
d
2
=
?
=
d
t
=
1
d_2=\cdots=d_t=1
d2?=?=dt?=1,
- p p p 在 Z m 1 ? \mathbb Z_{m_1}^* Zm1??? 的阶,就是 p p p 在 Z m ? \mathbb Z_m^* Zm?? 的阶 d d d
- g i , ? i ≥ 2 g_i,\forall i\ge 2 gi?,?i≥2 在 Z m ? \mathbb Z_m^* Zm?? 的阶,就是 g ˉ i \bar g_i gˉ?i? 在 Z m i ? / ( p d ) = Z m i ? \mathbb Z_{m_i}^*/(p^d)=\mathbb Z_{m_i}^* Zmi???/(pd)=Zmi??? 的阶 k i k_i ki?
- k 1 = ? ( m 1 ) / d k_1=\phi(m_1)/d k1?=?(m1?)/d, k i = ? ( m i ) , ? i ≥ 2 k_i=\phi(m_i),\forall i\ge 2 ki?=?(mi?),?i≥2
[HS15] 将编码解码的线性变换视为多项式的多点求值。利用 [LPR13] 的 Powerful Basis,存在如下的同构:
R
p
r
:
=
Z
[
X
]
/
(
p
r
,
Φ
m
(
X
)
)
?
R
p
r
′
:
=
Z
[
X
1
,
?
?
,
X
t
]
/
(
p
r
,
Φ
m
1
(
X
)
,
?
?
,
Φ
m
t
(
X
)
)
R_{p^r}:=\mathbb Z[X]/(p^r,\Phi_m(X)) \cong R_{p^r}':=\mathbb Z[X_1,\cdots,X_t]/(p^r,\Phi_{m_1}(X),\cdots,\Phi_{m_t}(X))
Rpr?:=Z[X]/(pr,Φm?(X))?Rpr′?:=Z[X1?,?,Xt?]/(pr,Φm1??(X),?,Φmt??(X))
其同构映射为
X
i
?
X
m
/
m
i
X_i \mapsto X^{m/m_i}
Xi??Xm/mi?。由于
E
E
E 包含
m
m
m-th 本原单位根
ζ
\zeta
ζ,我们定义
ζ
i
:
=
ζ
m
/
m
i
\zeta_i:=\zeta^{m/m_i}
ζi?:=ζm/mi?,那么
α
(
ζ
h
)
=
α
′
(
ζ
1
h
1
,
?
?
,
ζ
t
h
t
)
\alpha(\zeta^h) = \alpha'(\zeta_1^{h_1},\cdots,\zeta_t^{h_t})
α(ζh)=α′(ζ1h1??,?,ζtht??),其中
h
=
CRT
(
h
1
,
?
?
,
h
t
)
∈
S
h=\text{CRT}(h_1,\cdots,h_t) \in S
h=CRT(h1?,?,ht?)∈S,并且
h
i
=
g
i
e
i
∈
S
i
h_i=g_i^{e_i} \in S_i
hi?=giei??∈Si?
现在,我们对
α
′
(
X
1
,
?
?
,
X
t
)
\alpha'(X_1,\cdots,X_t)
α′(X1?,?,Xt?) 在多个点
(
ζ
1
h
1
,
?
?
,
ζ
t
h
t
)
(\zeta_1^{h_1},\cdots,\zeta_t^{h_t})
(ζ1h1??,?,ζtht??) 上求值(效果是 Slot-to-Coeff):
α
′
(
X
1
,
?
?
,
X
t
)
=
∑
j
1
,
j
2
,
?
?
,
j
t
c
j
1
,
j
2
,
?
?
,
j
t
?
X
1
j
1
X
2
j
2
?
X
t
j
t
=
∑
j
2
,
?
?
,
j
t
(
∑
j
1
c
j
1
,
j
2
,
?
?
,
j
t
?
X
1
j
1
)
?
X
2
j
2
?
X
t
j
t
\begin{aligned} \alpha'(X_1,\cdots,X_t) &= \sum_{j_1,j_2,\cdots,j_t} c_{j_1,j_2,\cdots,j_t}\cdot X_1^{j_1}X_2^{j_2}\cdots X_t^{j_t}\\ &= \sum_{j_2,\cdots,j_t} \left(\sum_{j_1} c_{j_1,j_2,\cdots,j_t}\cdot X_1^{j_1}\right)\cdot X_2^{j_2}\cdots X_t^{j_t} \end{aligned}
α′(X1?,?,Xt?)?=j1?,j2?,?,jt?∑?cj1?,j2?,?,jt???X1j1??X2j2???Xtjt??=j2?,?,jt?∑?(j1?∑?cj1?,j2?,?,jt???X1j1??)?X2j2???Xtjt???
其中 j i ∈ [ ? ( m i ) ] j_i \in [\phi(m_i)] ji?∈[?(mi?)](考虑下 ? ( m ) \phi(m) ?(m) 的分解),因此关于 X 1 X_1 X1? 的每个小多项式的长度为 ? ( m 1 ) \phi(m_1) ?(m1?),共有 ? ( m ) / ? ( m 1 ) \phi(m)/\phi(m_1) ?(m)/?(m1?) 个小多项式。
[HS15] 采取的编码方式是,将它们的连续 d d d 个系数打包在单个槽内,总共需要 ? ( m 1 ) / d \phi(m_1)/d ?(m1?)/d 个明文槽。恰好我们选择的参数下,包含 ? ( m ) / ? ( m 1 ) \phi(m)/\phi(m_1) ?(m)/?(m1?) 条长度为 k 1 = ? ( m 1 ) / d k_1=\phi(m_1)/d k1?=?(m1?)/d 的维度 1 1 1 超列,因此每条维度 1 1 1 的超列都记录一个小多项式。
[HS15] 定义了 Eval 线性变换,它用于多点求值 α ′ ( X 1 , ? ? , X t ) \alpha'(X_1,\cdots,X_t) α′(X1?,?,Xt?),共分为 t t t 个截断,
-
第 1 1 1 阶段,小多项式 P j 2 , ? ? , j t ( X 1 ) = ∑ j 1 c j 1 , j 2 , ? ? , j t ? X 1 j 1 P_{j_2,\cdots,j_t}(X_1) = \sum_{j_1} c_{j_1,j_2,\cdots,j_t}\cdot X_1^{j_1} Pj2?,?,jt??(X1?)=∑j1??cj1?,j2?,?,jt???X1j1?? 存放在索引 ( ? , j 2 , ? ? , j t ) (\star,j_2,\cdots,j_t) (?,j2?,?,jt?) 的维度 1 1 1 超列,
-
关于多点 ζ 1 g 1 e 1 , 0 ≤ e 1 < k 1 \zeta_1^{g_1^{e_1}},0\le e_1<k_1 ζ1g1e1???,0≤e1?<k1? 的求值可以写作某线性变换 M 1 : Z p r d ? k 1 → E k 1 M_1: \mathbb Z_{p^r}^{d\cdot k_1} \to E^{k_1} M1?:Zprd?k1??→Ek1?(多项式的系数表示就是 power basis 下的坐标),可以利用 [HS18] 的 BSGS 技巧
-
计算结果是各个 e 1 e_1 e1? 索引的更少变元的若干多项式
A e 1 = α ′ ( ζ 1 g 1 e 1 , X 2 , ? ? , X t ) A_{e_1} = \alpha'(\zeta_1^{g_1^{e_1}},X_2,\cdots,X_t) Ae1??=α′(ζ1g1e1???,X2?,?,Xt?)
它的系数存放在索引 ( e 1 , ? , ? ? , ? ) (e_1,\star,\cdots,\star) (e1?,?,?,?) 的子超立方
-
-
第 2 2 2 阶段,我们将 A e 1 A_{e_1} Ae1?? 继续拆分为关于 X 2 X_2 X2? 的小多项式求值,
A e 1 ( X 2 , ? ? , X t ) = ∑ j 2 , j 3 , ? ? , j t P j 2 , j 3 , ? ? , j t ( ζ 1 g 1 e 1 ) ? X 2 j 2 X 3 j 3 ? X t j t = ∑ j 2 , j 3 , ? ? , j t ( ∑ j 2 P j 2 , j 3 , ? ? , j t ( ζ 1 g 1 e 1 ) ? X 2 j 2 ) ? X 3 j 3 ? X t j t \begin{aligned} A_{e_1}(X_2,\cdots,X_t) &= \sum_{j_2,j_3,\cdots,j_t} P_{j_2,j_3,\cdots,j_t}(\zeta_1^{g_1^{e_1}})\cdot X_2^{j_2}X_3^{j_3}\cdots X_t^{j_t}\\ &= \sum_{j_2,j_3,\cdots,j_t} \left(\sum_{j_2} P_{j_2,j_3,\cdots,j_t}(\zeta_1^{g_1^{e_1}})\cdot X_2^{j_2}\right)\cdot X_3^{j_3}\cdots X_t^{j_t} \end{aligned} Ae1??(X2?,?,Xt?)?=j2?,j3?,?,jt?∑?Pj2?,j3?,?,jt??(ζ1g1e1???)?X2j2??X3j3???Xtjt??=j2?,j3?,?,jt?∑?(j2?∑?Pj2?,j3?,?,jt??(ζ1g1e1???)?X2j2??)?X3j3???Xtjt???
这些小多项式 Q e 1 , j 3 , ? ? , j t ( X 2 ) Q_{e_1,j_3,\cdots,j_t}(X_2) Qe1?,j3?,?,jt??(X2?) 被存放在索引 ( e 1 , ? , j 3 , ? ? , j t ) (e_1,\star,j_3,\cdots,j_t) (e1?,?,j3?,?,jt?) 的维度 2 2 2 超列,类似地执行线性变换 M 2 M_2 M2? 计算出它们,获得索引 ( e 1 , e 2 , ? , ? ? , ? ) (e_1,e_2,\star,\cdots,\star) (e1?,e2?,?,?,?) 的子超立方 -
对于 3 , ? ? , t 3,\cdots,t 3,?,t 阶段,也是类似的
对于 Coeff-to-Slot 过程,就是上述 Eval 变换的逆过程。
由于 digit-extraction 是作用在明文槽基环 Z p e + r \mathbb Z_{p^{e+r}} Zpe+r? 上的,因此需要利用 Frobenius map 构造 E E E-线性映射的线性化多项式,将明文槽内的各个 power basis 的系数分解到 d d d 个 “稀疏打包”(明文仅在基环内)的密文。现在可以执行数字提取了,最后还需将 d d d 个密文重新组合为 “密集打包” 的单个密文,从而可执行 Eval 运算。
当然,[HS15] 也参考 [CH18] 给出了 “薄自举”,也就是明文本身就是稀疏打包的,此时可以将比特提取的过程减少为单个密文,效率基本提升了 d d d 倍(线性变换很快,主要是比特提取)。
Parameters for Recryption
在使用 HElib 时,需要设置合适的参数,使之支持自举程序。然而它并没有提供参数生成的程序。参数集应当满足的条件是:设置特征
p
p
p 和明文槽长度
n
n
n
- m m m 和 p p p 互素,从而 p p p 是 Z m ? \mathbb Z_m^* Zm?? 中的元素
- p p p 模 m m m 的乘法阶 d d d 被 n n n 整除,从而 E E E 中存在维度 n n n 的子环
- m m m 被分解为素数幂 m 1 , ? ? , m t m_1,\cdots,m_t m1?,?,mt?,存在某个 m i ? m_{i^*} mi?? 使得 p p p 模 m i ? m_{i^*} mi?? 的乘法阶也是 d d d,从而 Z m ? / ( p ) \mathbb Z_m^*/(p) Zm??/(p) 的阶是 k = ? ( m ) / d k=\phi(m)/d k=?(m)/d
- 重排使得 m i ? m_{i^*} mi?? 成为 m 1 m_1 m1?,计算循环群 Z m 1 ? / ( p ) \mathbb Z_{m_1}^*/(p) Zm1???/(p) 的生成元 g ˉ 1 \bar g_1 gˉ?1? 和阶 l 1 l_1 l1?,然后用 CRT 提升为 Z m ? \mathbb Z_m^* Zm?? 的生成元 g 1 g_1 g1?
- 对于 i > 1 i>1 i>1,继续计算循环群 Z m i ? / ( p d ) \mathbb Z_{m_i}^*/(p^d) Zmi???/(pd) 的生成元 g ˉ i \bar g_i gˉ?i? 和阶 l i l_i li?,然后用 CRT 提升为 Z m ? \mathbb Z_m^* Zm?? 的生成元 g i g_i gi?
- 事实上 p d ( m o d m i ) = 1 p^d \pmod{m_i}=1 pd(modmi?)=1,因此 g i , ? i > 2 g_i, \forall i>2 gi?,?i>2 在模 m m m 下的阶就等于在模 m i m_i mi? 下的阶(good dimension),从而超立方的一维旋转是高效的
HElib要求将 o r d ( g i ? m o d ? m i ) = o r d ( g i ? m o d ? m ) ord(g_i \bmod m_i)=ord(g_i \bmod m) ord(gi?modmi?)=ord(gi?modm) 的排在最前面,因此将上述结果反序
[HS15] 测试了一些参数下的性能,
- “thick” 版本的自举:用于稠密打包的明文,耗时较多。

- “thin” 版本的自举:专用于稀疏打包的明文,计算效率提高了大约 d d d 倍。它需要先执行 Slot-to-Coeff 变换(Froward-DFT),因此要求 min capacity 剩余;在末尾不执行它,因此 after capacity 也相对更大。

CH18
[HS15] 的比特提取程序的复杂度严重依赖明文模数
p
r
p^r
pr 的规模,对于较大的明文规模速度很慢。[CH18] 提出了更适合较大明文模数的自举算法,并给出 BFV 的第一个自举实现。此外,[CH18] 提出了 “瘦模式” 的自举,也就是 HElib 中的 “薄自举”。
Digit Removal Algorithm
[HS15] 采用 lifting polynomials 在 LSD 高位依次插入零,而 [CH18] 使用 lowest digit removal polynomials 直接计算出 LSD
简记 u i , j u_{i,j} ui,j? 表示 u [ i ] + ( p i + j + 1 ) u[i]+(p^{i+j+1}) u[i]+(pi+j+1) 等价类,或者说 u [ i ] ( m o d p i + j + 1 ) u[i]\pmod{p^{i+j+1}} u[i](modpi+j+1)

在 [GHS12] 和 [HS15] 的比特提取程序中,利用 F e ( X ) F_e(X) Fe?(X) 从 u i , 0 u_{i,0} ui,0?(绿色数字)迭代计算出 u i , e ? i ? 1 u_{i,e-i-1} ui,e?i?1?(同一行的蓝色数字),然后从 u u u 中减去 u k , i + 1 ? k ? p k , k ≤ i u_{k,i+1-k}\cdot p^{k},k\le i uk,i+1?k??pk,k≤i(所在的反对角线)获得 u i + 1 , 0 u_{i+1,0} ui+1,0?(下一行的绿色数字)。
在上述运算中, u 0 , e ? 1 = F e e ? 1 ( u 0 , 0 ) u_{0,e-1}=F_e^{e-1}(u_{0,0}) u0,e?1?=Fee?1?(u0,0?),由于 F e ( X ) F_e(X) Fe?(X) 本身就是 p p p 次多项式,因此计算 u 0 , e ? 1 u_{0,e-1} u0,e?1? 的多项式度数是 p e ? 1 p^{e-1} pe?1,需要的乘法深度较大(度数更大,乘法数量不一定多,但是乘法深度一定大)。
[CH18] 指出:对于任意素数
p
p
p 和指数
e
≥
1
e \ge 1
e≥1,从存在度数至多
(
e
?
1
)
(
p
?
1
)
+
1
(e-1)(p-1)+1
(e?1)(p?1)+1 的多项式
f
(
x
)
f(x)
f(x),它将整数
0
≤
x
<
p
e
0 \le x < p^e
0≤x<pe 映射为
f
(
x
)
≡
x
?
[
x
]
p
(
m
o
d
p
e
)
f(x) \equiv x-[x]_p \pmod{p^e}
f(x)≡x?[x]p?(modpe)
它可以直接移除 LSD(不过它无法移除其他的 digits,因此依旧需要和 lifting polynomials 组合使用),从而
g
(
x
)
:
=
x
?
f
(
x
)
g(x):=x-f(x)
g(x):=x?f(x) 就是提取 LSB 的度数至多
(
e
?
1
)
(
p
?
1
)
+
1
(e-1)(p-1)+1
(e?1)(p?1)+1 的多项式。
这个多项式的具体构造:首先定义如下的函数,
F
A
(
x
)
:
=
∑
j
=
0
∞
(
?
1
)
j
(
A
+
j
?
1
j
)
(
x
A
+
j
)
F_A(x) := \sum_{j=0}^\infty (-1)^j {A+j-1 \choose j}{x \choose A+j}
FA?(x):=j=0∑∞?(?1)j(jA+j?1?)(A+jx?)
它的功能是将
M
≥
A
M\ge A
M≥A 映射到
F
A
(
M
)
=
1
F_A(M)=1
FA?(M)=1,其余的是
F
A
(
M
)
=
0
F_A(M)=0
FA?(M)=0(一个输入固定为
A
A
A 的比较函数)
我们继续定义如下函数,其中的系数
a
(
m
)
a(m)
a(m) 是
F
p
,
F
2
p
,
?
F_{p},F_{2p},\cdots
Fp?,F2p?,? 的
x
m
x^m
xm 系数累加,
f
^
(
x
)
=
p
∑
j
=
1
∞
F
j
p
(
x
)
=
∑
m
=
p
∞
a
(
m
)
(
x
m
)
\hat f(x) = p\sum_{j=1}^\infty F_{jp}(x) = \sum_{m=p}^\infty a(m){x \choose m}
f^?(x)=pj=1∑∞?Fjp?(x)=m=p∑∞?a(m)(mx?)
它的功能是计算
max
?
k
{
x
≥
k
p
}
\max_k\{x\ge kp\}
maxk?{x≥kp} 或者说
x
?
[
x
]
p
x-[x]_p
x?[x]p?
我们实际只需要
x
?
[
x
]
p
(
m
o
d
p
e
)
x-[x]_p \pmod{p^e}
x?[x]p?(modpe) 等价类,而非
x
?
[
x
]
p
∈
Z
x-[x]_p \in \mathbb Z
x?[x]p?∈Z 本身,因此只需要它的有限截断(更高的那些
x
m
x^m
xm 不再影响
u
[
e
?
1
:
0
]
u[e-1:0]
u[e?1:0] 内的数据):
f
(
x
)
=
∑
m
=
p
(
e
?
1
)
(
p
?
1
)
+
1
a
(
m
)
(
x
m
)
f(x) = \sum_{m=p}^{(e-1)(p-1)+1} a(m){x \choose m}
f(x)=m=p∑(e?1)(p?1)+1?a(m)(mx?)
利用上述构造的
f
(
x
)
,
g
(
x
)
f(x),g(x)
f(x),g(x),假定我们想要移除最低的
v
v
v 个数位,那么需要计算出
u
[
0
]
(
m
o
d
p
e
)
,
u
[
1
]
(
m
o
d
p
e
?
1
)
,
?
?
,
u
[
v
?
1
]
(
m
o
d
p
e
?
v
)
u[0] \pmod{p^e},u[1]\pmod{p^{e-1}},\cdots,u[v-1]\pmod{p^{e-v}}
u[0](modpe),u[1](modpe?1),?,u[v?1](modpe?v),计算过程为:根据
u
i
,
0
u_{i,0}
ui,0?(绿色数字)直接计算
g
(
x
)
g(x)
g(x) 获得
u
i
,
e
?
i
?
1
u_{i,e-i-1}
ui,e?i?1?(红色数字),还需迭代计算
F
e
F_e
Fe? 获得
u
i
,
v
?
i
?
1
u_{i,v-i-1}
ui,v?i?1?(同一行的蓝色数字)用于获取
u
i
+
1
,
0
u_{i+1,0}
ui+1,0?(下一行的绿色数字)。

复杂度分析:
- 为了计算 u i , 0 u_{i,0} ui,0?,需要 u u u 减去反对角线上的那些数字, u 0 , i = F e i ( u ) u_{0,i}=F_e^i(u) u0,i?=Fei?(u) 的次数为 p i p^i pi, , u 1 , i ? 1 = F e i ? 1 ( u 1 , 0 ) , u_{1,i-1}=F_e^{i-1}(u_{1,0}) ,u1,i?1?=Fei?1?(u1,0?) 的次数也是 p i p^i pi,其他的也都是,因此计算 u i , 0 u_{i,0} ui,0? 的多项式次数为 p i p^i pi
- 在 [HS15] 方法中,计算 u i , e ? i ? 1 u_{i,e-i-1} ui,e?i?1? 需要计算 F e e ? i ? 1 ( u i , 0 ) F_e^{e-i-1}(u_{i,0}) Fee?i?1?(ui,0?),它自身的次数为 p e ? i ? 1 p^{e-i-1} pe?i?1,总的度数为 p e ? 1 p^{e-1} pe?1
- 在 [CH18] 方法中,计算 u i , e ? i ? 1 u_{i,e-i-1} ui,e?i?1? 需要计算 g ( u i , 0 ) g(u_{i,0}) g(ui,0?),它自身的次数仅为 ( p ? 1 ) ( e ? i ? 1 ) + 1 (p-1)(e-i-1)+1 (p?1)(e?i?1)+1,总的度数为 e p v ep^{v} epv
- 当 v ≤ e ? 1 v \le e-1 v≤e?1 并且 p > e p>e p>e 时(较大的明文模数),[CH18] 的方法复杂度更低
如果计算某些蓝色数字时,满足了条件 p l > ( p ? 1 ) ( e ? i ? 1 ) + 1 p^l>(p-1)(e-i-1)+1 pl>(p?1)(e?i?1)+1,那么可以直接使用红色数字(比同一行的蓝色数字含有更多的高位零,因此必定是正确的)来构造下一行的绿色数字,多项式的度数会更低。[CH18] 的数位移除程序为:

Bootstrapping for FV and BGV
对于 BGV 自举:
- 密文模数需要和明文特征互素,选取 q = p e + 1 q=p^e+1 q=pe+1
- 相位
[
p
r
v
+
m
]
q
[p^rv+m]_{q}
[prv+m]q?,
- 明文放大 p p p 倍:计算 c t ? [ p ] q ct \cdot [p]_q ct?[p]q?,相位变为 [ p r + 1 v + p m ] q [p^{r+1}v+pm]_{q} [pr+1v+pm]q?
- 明文缩小 p p p 倍(要求 p ∣ m p \mid m p∣m):计算 c t ? [ p ? 1 ] q ct \cdot [p^{-1}]_q ct?[p?1]q?,相位变为 [ p r ? 1 v + m / p ] q [p^{r-1}v+m/p]_{q} [pr?1v+m/p]q?
对于 BFV 自举:
- 密文模数和明文特征之间没有要求,选取 q = p e q=p^e q=pe
- 相位
[
p
e
?
r
m
+
v
]
q
[p^{e-r}m+v]_q
[pe?rm+v]q?,
- 明文放大 p p p 倍:将 Δ = p e ? r \Delta=p^{e-r} Δ=pe?r 修改为 Δ ′ = p e ? r ? 1 \Delta'=p^{e-r-1} Δ′=pe?r?1,相位依旧是 [ p e ? r ? 1 ? p m + v ] q [p^{e-r-1}\cdot pm+v]_q [pe?r?1?pm+v]q?
- 明文缩小 p p p 倍(要求 p ∣ m p \mid m p∣m):将 Δ = p e ? r \Delta=p^{e-r} Δ=pe?r 修改为 Δ ′ = p e ? r + 1 \Delta'=p^{e-r+1} Δ′=pe?r+1,相位依旧是 [ p r ? 1 + 1 ? m / p + v ] q [p^{r-1+1}\cdot m/p + v]_{q} [pr?1+1?m/p+v]q?
采取 [HS15] 对 BGV 自举的框架,[CH18] 对于 BFV 自举的框架为:

此外,[CH18] 对于 “稀疏打包” 的明文,提出了 “slim mode” 版本的自举。需要注意的是,它首先在待自举的密文上执行 Slot-to-Coeff 线性变换,因此要求输入密文的 Level 不能被消耗殆尽,必须能够支撑这个线性变换。当然,它的数字提取之后不必执行 Slot-to-Coeff 变换,因此输出密文的 Level 也会稍大一点。

效率对比:对于 e ≥ v + 2 e \ge v+2 e≥v+2 以及较大的 p p p,[CH18] 的方法更好,
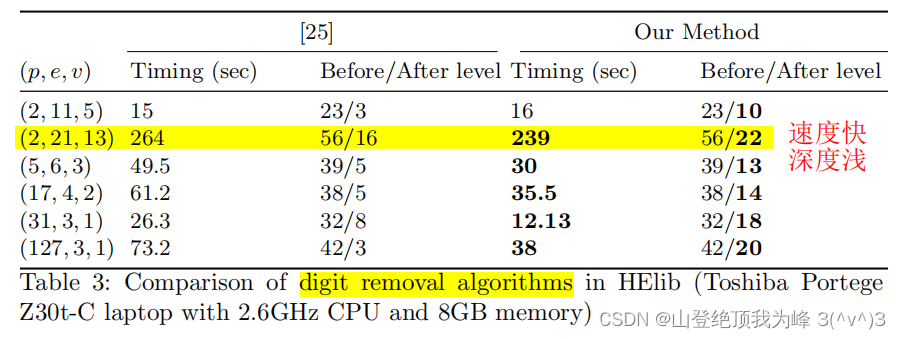
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- String转JSON Object
- linuxc环形缓冲区代码
- windows虚拟机项目部署
- C++入门【26-C++ Null 指针】
- 软件测试----测试管理方法论
- 工作遇到问题与解决办法(二)
- React16源码: React中的IndeterminateComponent的源码实现
- Java在线学习系统的设计与开发(源码+开题)
- FastAdmin后台安装出现2054错误的解决办法
- 电子电器架构车载软件 —— 集中化架构软件开发