线段树/区间树(java实现版详解附leetcode例题)
目录
什么是线段树
在介绍线段树前,我们先通过两个小问题引入一下为什么我们需要使用线段树。
最经典的线段树问题:区间染色

或者我们更普遍的问一个问题:在m次操作后,我们可以在[i,j]区间 中我们可以看见多少种颜色?
对于这种问题,我们可以用数组实现两种操作:
染色操作(更新区间) O(n)
查询操作(查询区间) O(n)
O(n)的时间复杂度在一些情况下是不适合的,所以我们要进一步寻找更优的算法。
另一经典问题:区间查询
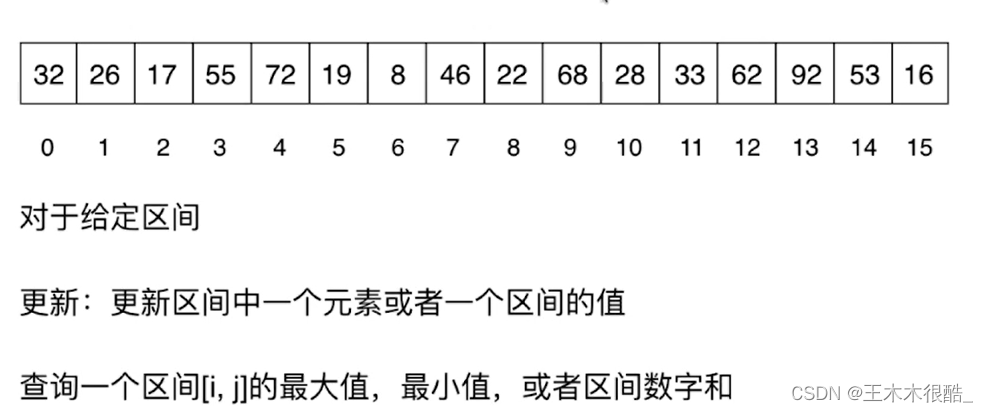
以上两种经典问题的更新和查询都是O(n)的时间复杂度,这时候引入线段树就显得额外宝贵了。?

在用一个数组A创建线段树时,我们有一个前提,就是对于我们的线段树,我们是不考虑向线段树中添加元素或者删除元素的,比如我们墙的长度给出来那它就是固定的了,我们不再考虑再加长或者缩短这面墙。这样我们就保证了区间本身是固定的,所以我们用静态数组就好了。

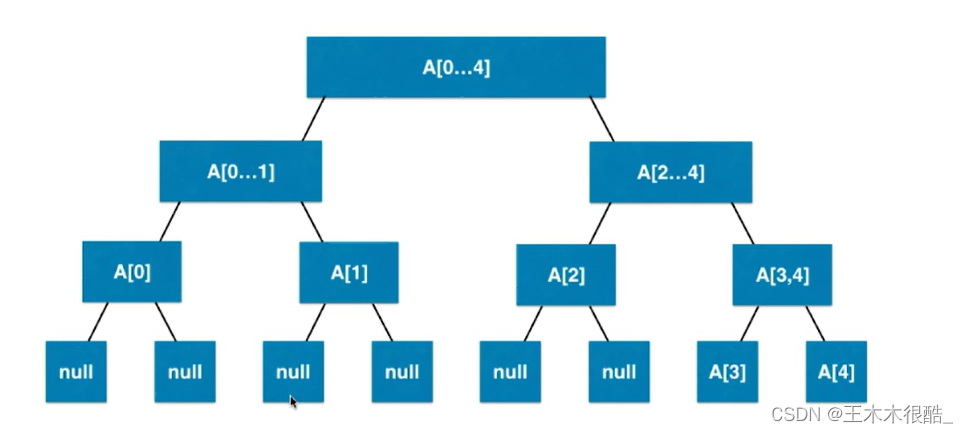
根据数组A构造的线段树就是下图的样子:

我们可以看到,线段树每个结点都是一个区间,这个区间不是说把区间中的所有元素都存进这个结点,以线段树求和为例,每个结点存储的就是它所在区间的数值和。例如:A[4...7]存储的就是[4,7]这个区间中所有数字的和。
线段树基础表示
线段树不一定是满二叉树,我们上面举得数组A构成的线段树中有8个元素,8刚好是2的3次方,所以它恰好是一棵满二叉树。一般情况下,如果某个结点的区间元素个数是偶数可以平分,那么一个结点的左右孩子各自会存储一半的元素。否则,就左右孩子一个存的少一点一个存的多一点。
例如一个存储10个元素的数组A就和8个元素的数组A不一样:

我们可以看到,线段树的叶子节点不一定在最后一层,也可以在倒数第二层。
我们的线段树也不一定是满二叉树,也不一定是完全二叉树。
但我们的线段树一定是一棵平衡二叉树(最大深度和最小深度的差不超过1)。
平衡二叉树的优势是:它不会像二分搜索树一样退化成一个链表,一棵平衡二叉树的高度和结点的关系一定是一个log的关系,这使得在平衡二叉树上进行搜索查询是非常高效的。
线段树虽然不是一个完全二叉树,但是作为一棵平衡二叉树,我们仍然可以用数组来表示它。表示方法是什么呢?我们可以把线段树看作是一棵满二叉树,最后一层虽然有很多结点是不存在的,我们把它们看作是空就好了。满二叉树作为一棵完全二叉树,是可以用数组来表示的。
如果区间有n个元素,用数组表示需要有多少结点呢?
对于一棵满二叉树,层数和每一层的结点数的关系是 第h - 1层 : 2^(h - 1)。

h层是指从0层到h-1层共h层。
有了上图所给的结论,我们就能很好的分析所需要的结点数了。

 ?
?
当然,对于这4n的空间,我们并不是每一个都利用起来了,而且我们是一个估计值,线段树不一定是满二叉树,最后一层的很多地方就是空的,在最坏的情况下可能有一半的空间都是浪费的,如下图。
不过我们在这里不用过多的考虑这些浪费的情况,对现代计算机来说存储空间本身还是不叫问题的,我们做算法的原则一般还是需要用空间来换时间。当然这些浪费是可以避免的,我们在文章最后对线段树做更多拓展的时候会提到,有兴趣的朋友可以尝试不使用数组来存储而采用链式的结构来存储线段树。
我们现在是采用数组的方式来存储一棵线段树,我们先实现一个基础的代码。
创建线段树(Java版详解)
//线段树的各自基本实现
public class SegmentTree<E> {
private E[] data;
private E[] tree;
private Merger<E> merger;
//构造函数传进来的是我们整个要考察的范围
public SegmentTree(E[] arr, Merger<E> merger){
this.merger = merger;
data = (E[])new Object[arr.length];
for(int i = 0; i < arr.length; i++){
data[i] = arr[i];
}
tree = (E[])new Object[4 * arr.length];
//从根节点开始
buildSegmentTree(0, 0, data.length - 1);
}
//在treeIndex的位置创建表示区间[l...r]的线段树
private void buildSegmentTree(int treeIndex, int l, int r){
if(l == r){
tree[treeIndex] = data[l];
return;
}
//左右子树对应的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
//左右子树对应的区间范围
int mid = l + (r - l) / 2; //防止整型溢出
//递归调用
buildSegmentTree(leftTreeIndex, l, mid);
buildSegmentTree(rightTreeIndex, mid + 1, r);
/*因为我们整体代码采用的是泛型,所以tree[treeIndex]的具体实现是加减乘除还是其他什么是取决于用户的具体实现
我们引入了一个接口融合器,否则直接写加减乘除还是怎样编译器会报错*/
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
public int getSize(){
return data.length;
}
public E get(int index){
if(index < 0 || index >= data.length){
throw new IllegalArgumentException("Index is illegal");
}
return data[index];
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子
private int leftChild(int index){
return 2 * index + 1;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子
private int rightChild(int index){
return 2 * index + 2;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append('[');
for(int i = 0; i < tree.length; i++){
if(tree[i] != null){
res.append(tree[i]);
}
else{
res.append("null");
}
if(i != tree.length - 1){
res.append(",");
}
}
res.append(']');
return res.toString();
}
}
//融合器接口实现
public interface Merger<E> {
E merge(E a, E b);
}//Main函数
//线段树结构的数组表示,以线段树求和为例
public class Main{
public static void main(String[]args){
Integer []nums = {-2, 0, 3, -5, 2, -1};
SegmentTree<Integer> segTree = new SegmentTree<>(nums, (a, b) -> a + b);
System.out.println(segTree);
}
}运行结果:

线段树的区间查询
线段树的查询还是蛮好理解的,只需要从根节点开始向下找相应的子区间,然后再把所有找到的子区间综合起来就好了?,这个找的过程和树的高度相关,和我们需要查询的区间长度是无关的。因为线段树的高度是logn级别的,所以我们整个的查询也是logn级别的。
接下来我们来实现一下线段树的查询操作:
//查询操作
//返回待查询区间[queryL, queryR]的值
public E query(int queryL, int queryR){
//边界检查
if(queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR){
throw new IllegalArgumentException("Index is illegal");
}
//递归函数,从根节点开始
return query(0, 0, data.length - 1, queryL, queryR);
}
//设计递归函数
//在以treeID为根的线段树中[l...r]的范围里,搜索区间[queryL...queryR]的值
private E query(int treeIndex, int l, int r, int queryL, int queryR){
if(l == queryL && r == queryR){
return tree[treeIndex];
}
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
//待查询区间落在右孩子那边
if(queryL >= mid + 1){
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
}
//落在左孩子那边
else if(queryR <= mid){
return query(leftTreeIndex, l, mid, queryL, queryR);
}
//一部分落在左孩子那边,一部分落在右孩子那边
E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
//两边都找一下然后融合
return merger.merge(leftResult, rightResult);
}
把我们刚实现的查询操作加入咱们线段树的基础代码中,并在main函数中创建样例运行。
//实现了查询操作的线段树基本操作
public class SegmentTree<E> {
private E[] data;
private E[] tree;
private Merger<E> merger;
//构造函数传进来的是我们整个要考察的范围
public SegmentTree(E[] arr, Merger<E> merger){
this.merger = merger;
data = (E[])new Object[arr.length];
for(int i = 0; i < arr.length; i++){
data[i] = arr[i];
}
tree = (E[])new Object[4 * arr.length];
//从根节点开始
buildSegmentTree(0, 0, data.length - 1);
}
//在treeIndex的位置创建表示区间[l...r]的线段树
private void buildSegmentTree(int treeIndex, int l, int r){
if(l == r){
tree[treeIndex] = data[l];
return;
}
//左右子树对应的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
//左右子树对应的区间范围
int mid = l + (r - l) / 2; //防止整型溢出
//递归调用
buildSegmentTree(leftTreeIndex, l, mid);
buildSegmentTree(rightTreeIndex, mid + 1, r);
/*因为我们整体代码采用的是泛型,所以tree[treeIndex]的具体实现是加减乘除还是其他什么是取决于用户的具体实现
我们引入了一个接口融合器,否则直接写加减乘除还是怎样编译器会报错*/
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}
public int getSize(){
return data.length;
}
public E get(int index){
if(index < 0 || index >= data.length){
throw new IllegalArgumentException("Index is illegal");
}
return data[index];
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子
private int leftChild(int index){
return 2 * index + 1;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子
private int rightChild(int index){
return 2 * index + 2;
}
//查询操作
//返回待查询区间[queryL, queryR]的值
public E query(int queryL, int queryR){
//边界检查
if(queryL < 0 || queryL >= data.length ||
queryR < 0 || queryR >= data.length || queryL > queryR){
throw new IllegalArgumentException("Index is illegal");
}
//递归函数,从根节点开始
return query(0, 0, data.length - 1, queryL, queryR);
}
//设计递归函数
//在以treeID为根的线段树中[l...r]的范围里,搜索区间[queryL...queryR]的值
private E query(int treeIndex, int l, int r, int queryL, int queryR){
if(l == queryL && r == queryR){
return tree[treeIndex];
}
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
//待查询区间落在右孩子那边
if(queryL >= mid + 1){
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
}
//落在左孩子那边
else if(queryR <= mid){
return query(leftTreeIndex, l, mid, queryL, queryR);
}
//一部分落在左孩子那边,一部分落在右孩子那边
E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
//两边都找一下然后融合
return merger.merge(leftResult, rightResult);
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append('[');
for(int i = 0; i < tree.length; i++){
if(tree[i] != null){
res.append(tree[i]);
}
else{
res.append("null");
}
if(i != tree.length - 1){
res.append(",");
}
}
res.append(']');
return res.toString();
}
}
/融合器
public interface Merger<E> {
E merge(E a, E b);
}
//线段树结构的数组表示,以线段树求和为例
public class Main{
public static void main(String[]args){
Integer []nums = {-2, 0, 3, -5, 2, -1};
SegmentTree<Integer> segTree = new SegmentTree<>(nums, (a, b) -> a + b);
//System.out.println(segTree);
System.out.println(segTree.query(0, 2));//查询区间为-2 + 0 + 3
System.out.println(segTree.query(0, 5));//查询区间为nums全加起来
}
}运行结果:

leetcode上的线段树相关问题
leetcode303题.区域和检索-数组不可变
303. 区域和检索 - 数组不可变 - 力扣(LeetCode)
这里的不可变指的是不涉及线段树的更新操作,什么是线段树的更新操作我们一会儿会讲。
给定一个整数数组 ?
nums,处理以下类型的多个查询:计算索引?
left?和?right?(包含?left?和?right)之间的?nums?元素的?和?,其中?left <= right实现?
NumArray?类:
NumArray(int[] nums)?使用数组?nums?初始化对象int sumRange(int i, int j)?返回数组?nums?中索引?left?和?right?之间的元素的?总和?,包含?left?和?right?两点(也就是?nums[left] + nums[left + 1] + ... + nums[right]?)示例 1:
输入: ["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]] 输出: [null, 1, -1, -3] 解释: NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]); numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3) numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))提示:
1 <= nums.length <= 10^4-105?<= nums[i] <=?10^50 <= i <= j < nums.length- 最多调用?
10^4次?sumRange?方法
使用线段树解题
class NumArray {
private int[] tree;
private int[] data;
private int left(int idx){
return 2*idx+1;
}
private int right(int idx){
return 2*idx+2;
}
private void buildSegmentTree(int treeIdx,int l,int r){
if(l==r){
tree[treeIdx]=data[l];
return;
}
int mid=l+(r-l)/2;
int leftTreeIndex=left(treeIdx);
int rightTreeIndex=right(treeIdx);
buildSegmentTree(leftTreeIndex,l,mid);
buildSegmentTree(rightTreeIndex,mid+1,r);
tree[treeIdx]=tree[leftTreeIndex]+tree[rightTreeIndex];
}
public NumArray(int[] nums) {
data=new int[nums.length];
for (int i = 0; i < nums.length; i++) {
data[i]=nums[i];
}
tree=new int[nums.length*4];
buildSegmentTree(0,0,data.length-1);
}
private int query(int idx,int l,int r,int qL,int qR){
if(l==qL&&r==qR)return tree[idx];
int mid=l+(r-l)/2;
int leftTree=left(idx);
int rightTree=right(idx);
if(qL>=mid+1)return query(rightTree,mid+1,r,qL,qR);
if(qR<=mid)return query(leftTree,l,mid,qL,qR);
int leftRes=query(leftTree,l,mid,qL,mid);
int rightRes=query(rightTree,mid+1,r,mid+1,qR);
return leftRes+rightRes;
}
public int sumRange(int left, int right) {
if(left<0||left>=data.length||right<0||right>=data.length||left>right)
throw new IllegalArgumentException("Idx is illegal.");
return query(0,0,data.length-1,left,right);
}
}
不使用线段树解题
//进行预处理
class NumArray {
//sum[i]存储前i个元素和,sum[0] = 0
//sum[i]存储nums[0...i - 1]的和
private int[]sum;
public NumArray(int[] nums) {
//因为sum[0]存储的不是第一个元素的值,只是一个数字0,sum[1]才是第一个元素的值,所以有一个偏移量
sum = new int[nums.length + 1];
sum[0] = 0;
for(int left = 1; left < sum.length; left++){
sum[left] = sum[left - 1] + nums[left - 1];
}
}
public int sumRange(int left, int right) {
//从0到right元素的和减去从0到left - 1对应的和
return sum[right + 1] - sum[left];
}
}
这么一看,好像不用线段树的方法更方便哎,那我们干嘛还用线段树?题目一开头我们说了,这道题不涉及线段树的更新操作,线段树更适合解决动态的情况,这道题所有的数值都是固定的、静态的,所以不用使用线段树这么复杂的数据结构就能解决。
让我们再来一道题作为静态的对比。
leetcode307题.区域和检索-数组可修改
307. 区域和检索 - 数组可修改 - 力扣(LeetCode)
给你一个数组?
nums?,请你完成两类查询。
- 其中一类查询要求?更新?数组?
nums?下标对应的值- 另一类查询要求返回数组?
nums?中索引?left?和索引?right?之间(?包含?)的nums元素的?和?,其中?left <= right实现?
NumArray?类:
NumArray(int[] nums)?用整数数组?nums?初始化对象void update(int index, int val)?将?nums[index]?的值?更新?为?valint sumRange(int left, int right)?返回数组?nums?中索引?left?和索引?right?之间(?包含?)的nums元素的?和?(即,nums[left] + nums[left + 1], ...,nums[right])示例 1:
输入: ["NumArray", "sumRange", "update", "sumRange"] [[[1, 3, 5]], [0, 2], [1, 2], [0, 2]] 输出: [null, 9, null, 8] 解释: NumArray numArray = new NumArray([1, 3, 5]); numArray.sumRange(0, 2); // 返回 1 + 3 + 5 = 9 numArray.update(1, 2); // nums = [1,2,5] numArray.sumRange(0, 2); // 返回 1 + 2 + 5 = 8提示:
1 <= nums.length <= 3 *?10^4?-100 <= nums[i] <= 1000 <= index < nums.length-100 <= val <= 1000 <= left <= right < nums.length- 调用?
update?和?sumRange?方法次数不大于?3 * 10^4?
我们可以看到这道题和303题唯一的区别就是多了一个update的更新操作,我们先用非线段树方法来试一试。
不使用线段树解题
//进行预处理
class NumArray {
//sum[i]存储前i个元素和,sum[0] = 0
//sum[i]存储nums[0...i - 1]的和
private int[]sum;
private int[]data;
public NumArray(int[] nums) {
data = new int[nums.length];
for(int i = 0; i < nums.length; i++){
data[i] = nums[i];
}
//因为sum[0]存储的不是第一个元素的值,只是一个数字0,sum[1]才是第一个元素的值,所以有一个偏移量
sum = new int[nums.length + 1];
sum[0] = 0;
for(int left = 1; left < sum.length; left++){
sum[left] = sum[left - 1] + nums[left - 1];
}
}
public void update(int index, int val) {
data[index] = val;
for(int left = index + 1; left < sum.length; left++){
sum[left] = sum[left - 1] + data[left - 1];
}
}
public int sumRange(int left, int right) {
//从0到right元素的和减去从0到left - 1对应的和
return sum[right + 1] - sum[left];
}
}
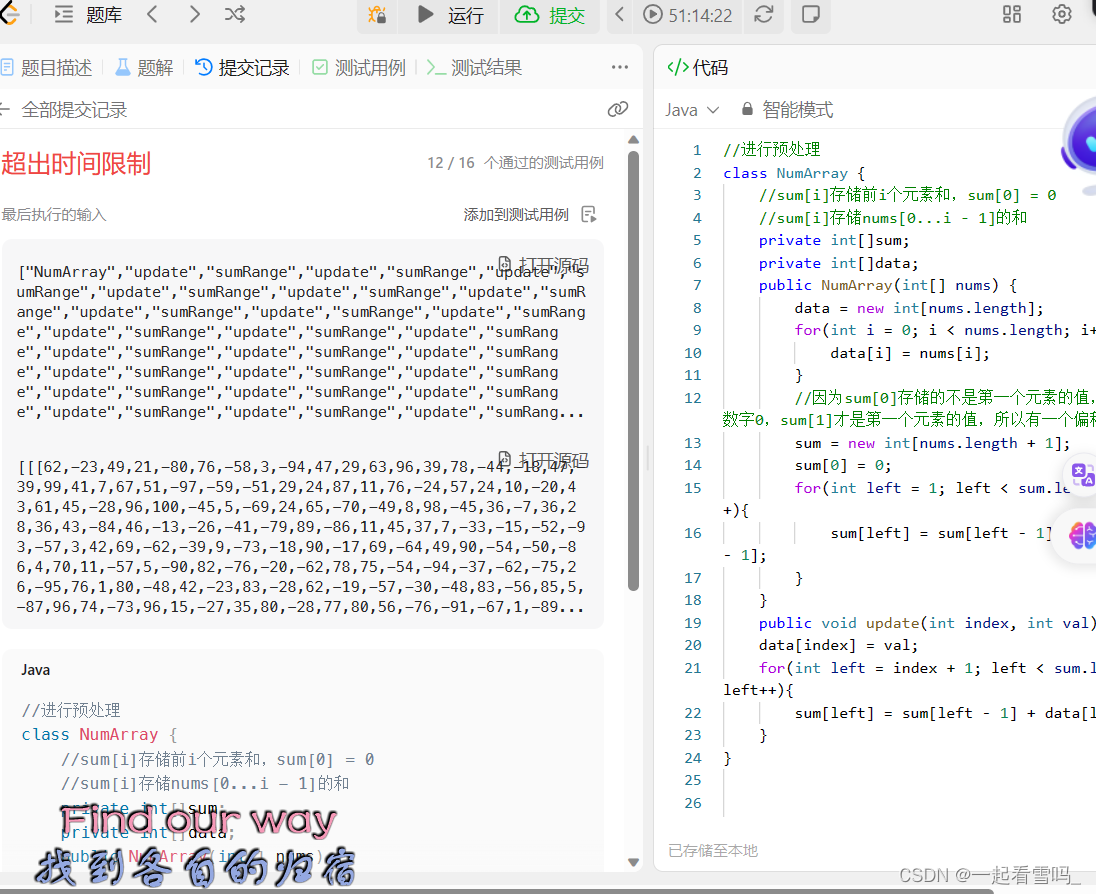 我们可以看到,非线段树的方法只通过了12/16个样例,样例再大一点就超出运行时间了。?究其根本就是运行中存在大量的时间复杂度为O(n)的update操作,整体时间复杂度就是m * n 级别,是比较慢的。此时我们的数组就需要动态的改变了,线段树这种数据结构就要发挥作用了,接下来我们就要在我们的线段树中添加上update的操作,然后进一步解决307号这个问题。(线段树方法的题解放后文)
我们可以看到,非线段树的方法只通过了12/16个样例,样例再大一点就超出运行时间了。?究其根本就是运行中存在大量的时间复杂度为O(n)的update操作,整体时间复杂度就是m * n 级别,是比较慢的。此时我们的数组就需要动态的改变了,线段树这种数据结构就要发挥作用了,接下来我们就要在我们的线段树中添加上update的操作,然后进一步解决307号这个问题。(线段树方法的题解放后文)
线段树中的更新操作
以下代码可以加入我们之前实现的线段树的基本操作。
//将index位置的值更新为e
public void set(int index, E e){
if(index < 0 || index >= data.length){
throw new IllegalArgumentException("Index is illegal");
}
data[index] = e;
//递归
set(0, 0, data.length - 1, index, e);
}
private void set(int treeIndex, int l, int r, int index, E e){
if(l == r){
tree[treeIndex] = e;
return;
}
int mid = l + (r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if(index >= mid + 1){
set(rightTreeIndex, mid + 1, r, index, e);
}
else{
set(leftTreeIndex, l, mid, index, e);
}
tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
}学会了线段树的更新操作后,我们就可以回过头来去解决307号问题的线段树解法。
使用线段树解题
class NumArray {
class TreeNode{
public int sum;
public int start, end;
public TreeNode left, right;
public TreeNode(int start, int end){
this.start = start;
this.end = end;
}
}
TreeNode root = null;
public NumArray(int[] nums) {
root = buildTree(nums, 0, nums.length - 1);
}
public void update(int index, int val) {
update(root, index, val);
}
public int sumRange(int left, int right) {
return query(root, left, right);
}
private int query(TreeNode root, int left, int right){
if(root.start == left && root.end == right)
return root.sum;
else{
int mid = root.start + (root.end - root.start) / 2;
if(right <= mid)
return query(root.left, left, right);
else if(left > mid)
return query(root.right, left, right);
else
return query(root.left, left, mid) + query(root.right, mid + 1, right);
}
}
private void update(TreeNode root, int index, int val){
if(root.start == root.end){
root.sum = val;
return;
}else{
int mid = root.start + (root.end - root.start) / 2;
if(index <= mid)
update(root.left, index, val);
else
update(root.right, index, val);
root.sum = root.left.sum + root.right.sum;
}
}
private TreeNode buildTree(int[] nums, int start, int end){
if(start > end)
return null;
else if(start == end){
TreeNode node = new TreeNode(start, end);
node.sum = nums[start];
return node;
}else{
TreeNode node = new TreeNode(start, end);
int mid = start + (end - start) / 2;
node.left = buildTree(nums, start, mid);
node.right = buildTree(nums, mid + 1, end);
node.sum = node.left.sum + node.right.sum;
return node;
}
}
}
更多线段树相关的话题

我们点了一下线段树的标签,发现leetcode上关于线段树的问题还挺难的。如果你不去参加算法竞赛的话,线段树不是一个重点,请合理安排自己的时间。
当我们赋予线段树合理的意义后,我们可以非常高效的处理和线段或者区间相关的问题。
我们实现的三个方法:创建线段树、查询线段树和更新线段树都采用了递归的写法。
懒惰更新
我们之前的更新操作都是对线段树某个结点存储的值进行的更新,但是如果我们想对区间进行更新呢?

我们可以使用一个lazy数组记录未更新的内容,大家有个印象就好,如果感兴趣可以自己去查阅资料学习。
二维线段树
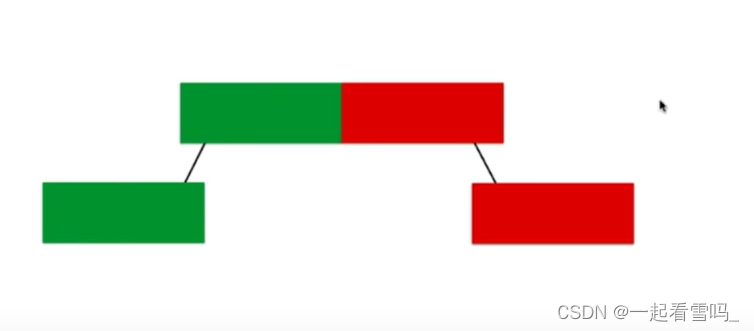
我们之前接触的都是上图所示的一维线段树,在一个坐标轴中的。可以分为前半段作为左孩子,右半段作为右孩子。
如果我们扩展到二维呢?

我们可以记录的是一个矩阵的内容,然后我们可以把矩阵分成四块,就可以有四个孩子,每个孩子就是一个更小的矩阵,直到在叶子结点的时候就只剩下一个元素,这就是二维线段树。
以此类推,我们还可以有三维线段树,那我们就可以分成八块.......
线段树本身就是一个思想,我们要学会把一个大的数据单元拆分成一个个小的数据单元,递归的表示这些数据,这本身就是树这种数据结构的实质。
动态线段树
我们上文说过,从数组方式存储开辟4n的空间免不了浪费,所以我们可以用链式的方式存储。
比如如果线段树的结点数非常大,比如一亿,那我们刚开始并不着急直接创造一个4*一亿的空间,而是动态的创建,用到哪里创哪里,如下图所示:
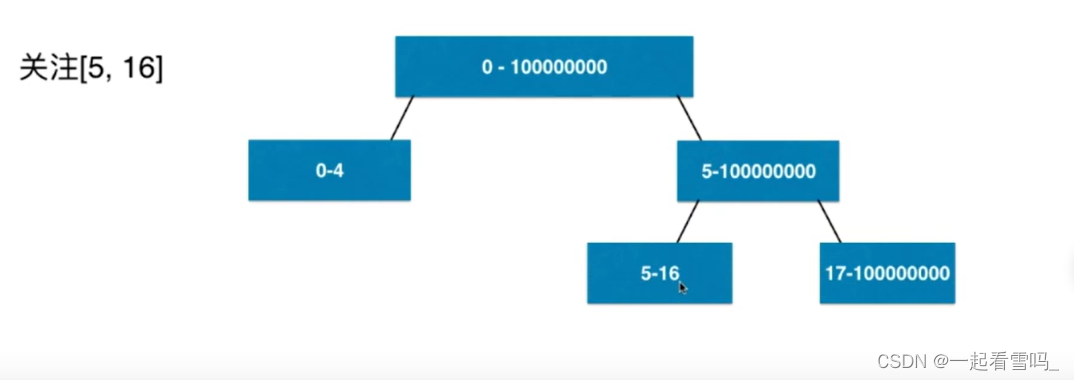
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Android 实现 Slots 游戏旋转效果
- Aspx漏洞总结
- Flutter类似于电力输送的动画
- 如何从github上下载代码
- 水果蔬菜销售系统(JSP+java+springmvc+mysql+MyBatis)
- 【网络安全 | Misc】Erik-Baleog-and-Olaf
- 面试算法110:所有路径
- element中Table表格控件单选、多选功能进一步优化
- YOLOv8改进 | 主干篇 | 低照度增强网络PE-YOLO改进主干(改进暗光条件下的物体检测模型)
- PageView组件实现翻页和自定义轮播图