动态规划——数字金字塔【集训笔记】

题目描述

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
?

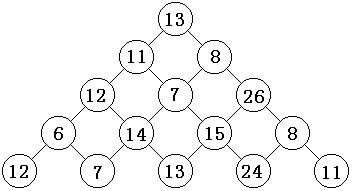
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。

输入

第一个行包含R(1≤ R≤1000)，表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。

输出

单独的一行，包含那个可能得到的最大的和。

样例输入1

5
13
11?8
12?7??26
6??14?15?8
12?7??13?24?11

样例输出1

86

提示/说明

标签

普及 其他 递归 递推 记忆化搜索 动态规划基础

方法一：

暴搜

时间超限67

方法二：

顺推

动规

状态转移方程：

向左走：f[i+1][j]>f[i][j]+a[i+1][j]?f[i+1][j]:f[i][j]+a[i+1][j]

向右走：f[i+1][j+1]>f[i][j]+a[i+1][j+1]?f[i+1][j+1]:f[i][j]+a[i+1][j+1]

代码：

#include<iostream>
using namespace std;
#define MAXN 1010
int a[MAXN][MAXN],f[MAXN][MAXN];
int n;
int main(){
    
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<i+1;j++){
            cin>>a[i][j];
        }
    }
    f[0][0]=a[0][0];
    for(int i=0;i<n-1;i++){
        for(int j=0;j<i+1;j++){
            f[i+1][j]=f[i+1][j]>f[i][j]+a[i+1][j]?f[i+1][j]:f[i][j]+a[i+1][j];
            f[i+1][j+1]=f[i+1][j+1]>f[i][j]+a[i+1][j+1]?f[i+1][j+1]:f[i][j]+a[i+1][j+1];
        }
    }
    int ans=f[n-1][0];
    for(int i=1;i<n;i++){
        ans=ans>f[n-1][i]?ans:f[n-1][i];
    }
    cout<<ans;
    return 0;
}

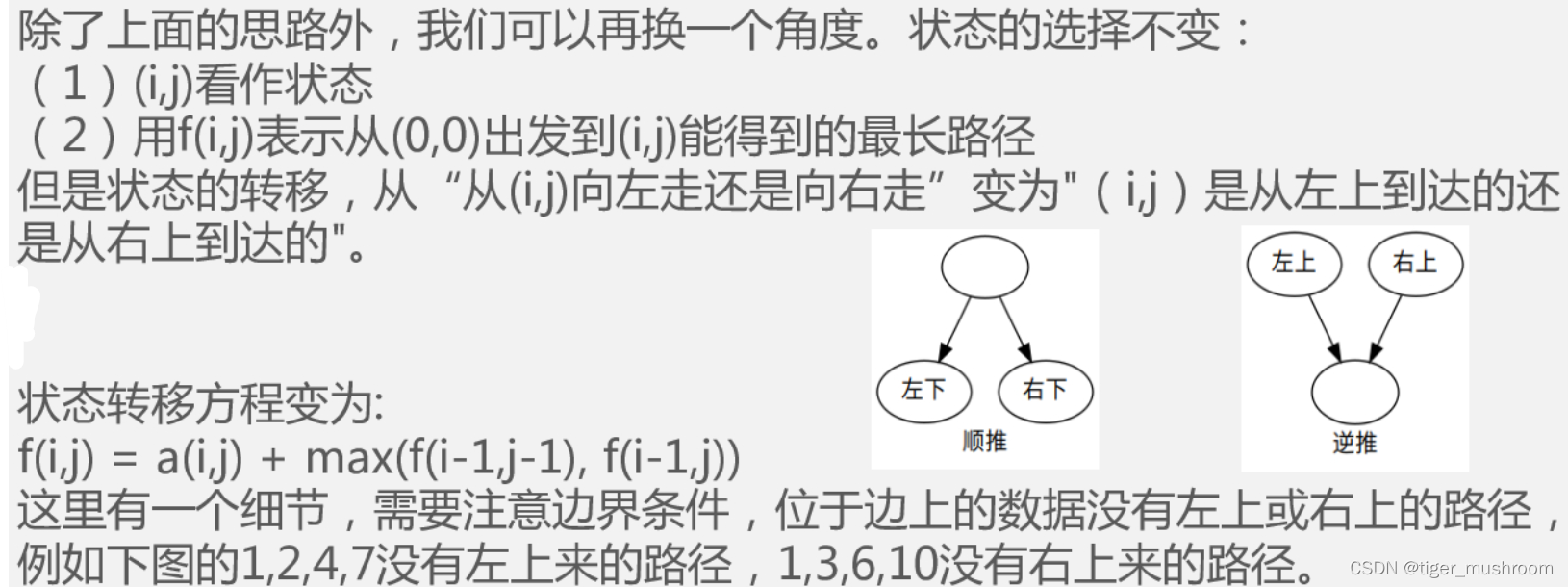
方法三：逆推

#include<iostream>
using namespace std;
int n;
int a[1005][1005],f[1005][1005];
int main(){
	cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<i+1;j++){
            cin>>a[i][j];
        }
    }
    for(int i=0;i<n;i++){
    	f[n-1][i]=a[n-1][i];
	}
	for(int i=n-2;i>=0;i--){
		for(int j=0;j<i+1;j++){
			f[i][j]=a[i][j]+(f[i+1][j]>f[i+1][j+1]?f[i+1][j]:f[i+1][j+1]);
		}
	}
	cout<<f[0][0];
	return 0;
}

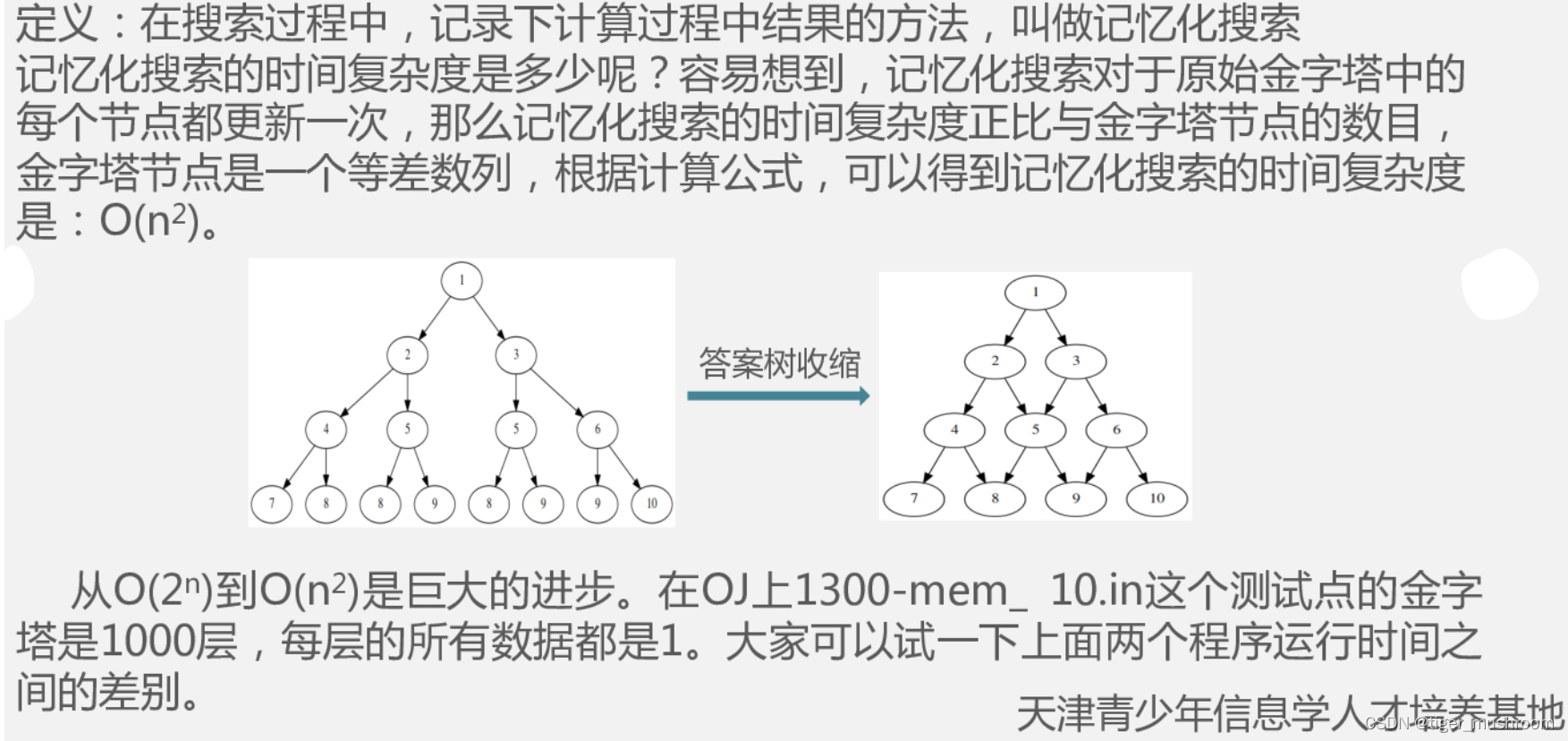
方法四：记忆化搜索