day22 二叉搜索树的最近公共祖先 二叉搜索树中的插入操作 删除二叉搜索树中的节点

题目1：235 二叉搜索树的最近公共祖先

题目链接：235 二叉搜索树的最近公共祖先

题意

找出二叉搜索树中两个指定节点的最近公共祖先

二叉搜索树中节点各不相同，且两个指定的节点均存在与二叉搜索树中，也不同

递归

递归三部曲：

1）递归函数的参数和返回值

2）终止条件

3）单层递归逻辑

使用二叉搜索树的性质：不用考虑前序,中序和后序遍历，直接使用二叉搜索树的性质，遇到目标节点直接返回

如果当前遍历的节点大于p，q，那么p和q公共祖先一定在该节点的左子树中，所以向左遍历；

如果当前遍历的节点小于p，q，那么p和q公共祖先一定在该节点的右子树中，所以向右遍历；

当前遍历的节点在p和q之间，那么当前节点一定是p和q的公共祖先，且一定是最近的公共祖先，因为p一定在左子树（右子树）中，q一定在右子树（左子树）中，所以当前遍历的节点一定是最近公共祖先

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
       //终止条件
       if(root==NULL) return NULL;
       //单层递归逻辑
       if(root->val>p->val && root->val>q->val){
           TreeNode* left = lowestCommonAncestor(root->left,p,q);
           if(left!=NULL) return left;
       } 
       if(root->val<p->val && root->val<q->val){
           TreeNode* right = lowestCommonAncestor(root->right,p,q);
           if(right!=NULL) return right;
       } 
       return root;
    }
};

迭代

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
       while(root!=NULL){
           if(root->val>p->val && root->val>q->val) root = root->left;
           else if(root->val<p->val && root->val<q->val) root = root->right;
           else return root;
       }
       return NULL;//没有找到
    }
};

题目2：701 二叉搜索树中的插入操作

题目链接：701 二叉搜索树中的插入操作

题意

将值value插入到二叉搜索树中，保证插入后的二叉树仍是二叉搜索树

插入任意一个节点都可以在叶子节点位置处找到该节点的位置，保证仍为二叉搜索树

递归

递归三部曲：

1）递归函数的参数和返回值

2）终止条件

3）单层递归逻辑

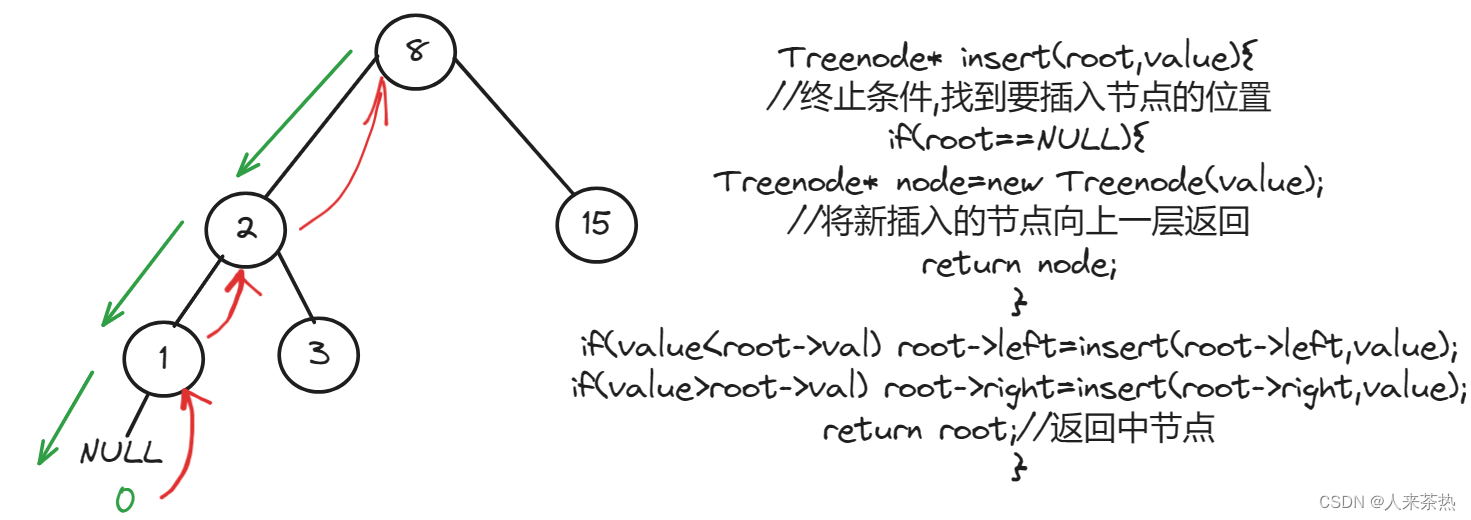
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        //终止条件,要插入的位置
        if(root==NULL){
            TreeNode* node = new TreeNode(val);
            return node;//将该节点返回给上一层
        }
        //单层递归逻辑
        if(root->val>val) root->left = insertIntoBST(root->left,val);
        if(root->val<val) root->right = insertIntoBST(root->right,val);
        return root;
    }
};

迭代

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root==NULL){
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* pre;//NULL节点的父节点
        TreeNode* cur = root;
        while(cur!=NULL){
            pre = cur;
            if(cur->val>val) cur = cur->left;
            else if(cur->val<val) cur = cur->right;
        }
        TreeNode* node = new TreeNode(val);
        if(pre->val>val) pre->left = node;
        else if(pre->val<val) pre->right = node;
        return root;
    }
};

题目3：450 删除二叉搜索树中的节点

题目链接：450 删除二叉搜索树中的节点

题意

删除二叉搜索树中值为key的节点，保证二叉树仍未二叉搜索树，

利用二叉树的性质，找到要删除的节点进行删除，不用遍历整棵二叉树

递归

递归三部曲：

1）递归函数的参数和返回值、

2）终止条件 找到要删除的节点

3）单层递归逻辑

伪代码

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        //终止条件
        //没有找到满足条件的节点
        if(root==NULL) return NULL;
        //找到满足条件的节点，分类讨论
        if(root->val==key){
            //叶子节点
            if(root->left==NULL && root->right==NULL) return NULL;
            //左子树为空，右子树不为空
            else if(root->left==NULL && root->right!=NULL) return root->right;
            //左子树不为空，右子树为空
            else if(root->left!=NULL && root->right==NULL) return root->left;
            //左子树和右子树都不为空
            else{
                TreeNode* cur = root->right;//右子树
                while(cur->left!=NULL) cur = cur->left;//右子树的最左侧叶子节点
                cur->left = root->left;//root的左子树移动到右子树最左侧叶子节点的左孩子
                //此时左为空，右不为空
                return root->right;
            }
        }
        //单层递归逻辑
        if(root->val>key) root->left = deleteNode(root->left,key);
        if(root->val<key) root->right = deleteNode(root->right,key);
        return root;
    }
};