常用的排序算法

该文章笔记结合菜鸟教程的排序算法，如果后面认识有改动或者完善再继续

最近笔试很多题目都考察过了基本的排序算法，尤其是快排、冒泡、选择，大家在这一方面一定要注意下。

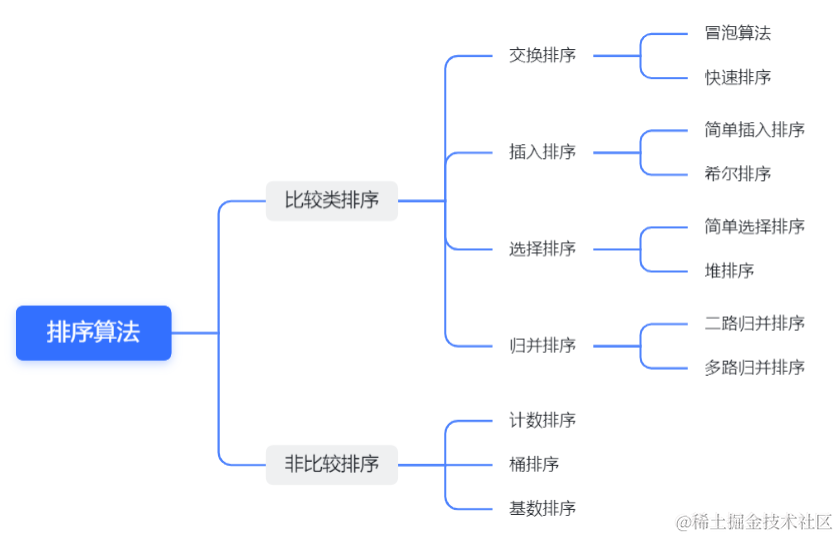
一. 总述

1. 时间复杂度

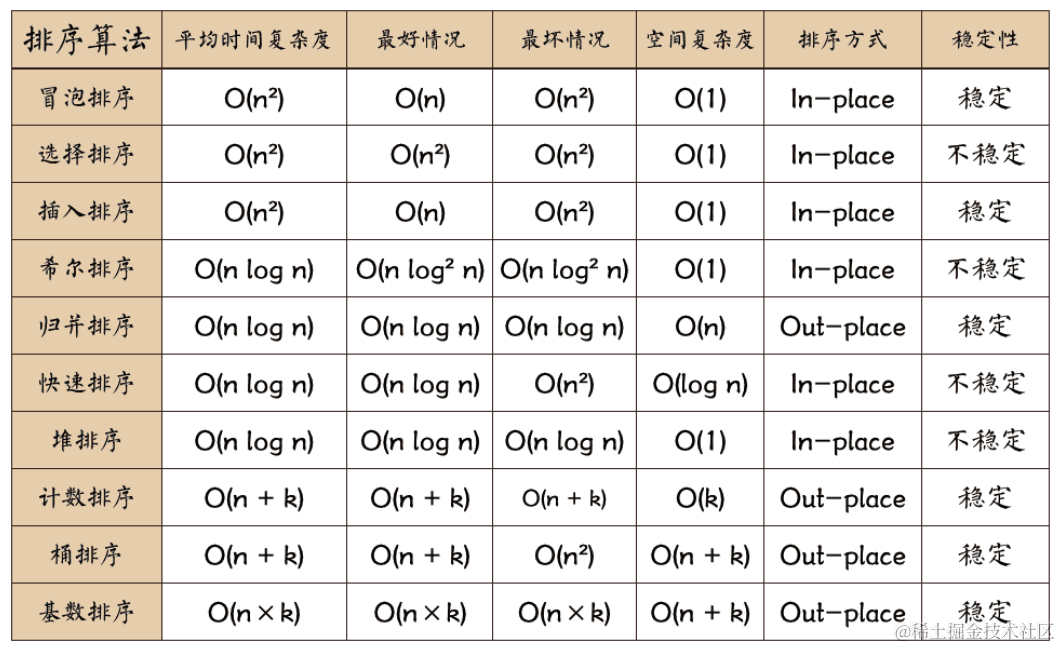
详细介绍

1. 冒泡排序

冒泡排序重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

具体步骤：

• 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较

代码实现：

        for (int i = 1; i < arr.length; i++) {
            // 设定一个标记，若为true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成。
            boolean flag = true;
            for (int j = 0; j < arr.length - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                    flag = false;
                }
            }
            if (flag) {
                break;
            }
        }
        return arr;

为什么不能贴动图啊，为什么啊

2. 选择排序

无论什么数据进去都是 O(n2) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处就是不占用额外的内存空间

具体步骤：

• 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
• 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
• 重复第二步，直到所有元素均排序完毕

代码实现：

        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        // 总共要经过 N-1 轮比较
        for (int i = 0; i < arr.length - 1; i++) {
            int min = i;

            // 每轮需要比较的次数 N-i
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    // 记录目前能找到的最小值元素的下标
                    min = j;
                }
            }

            // 将找到的最小值和i位置所在的值进行交换
            if (i != min) {
                int tmp = arr[i];
                arr[i] = arr[min];
                arr[min] = tmp;
            }

        }
        return arr;

3. 插入排序

插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

具体步骤：

• 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个当成是未排序序列。
• 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。
• （如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

代码实现：

        // 从下标为1的元素开始选择合适的位置插入，因为下标为0的只有一个元素，默认是有序的  
        for (int i = 1; i < arr.length; i++) {  
            // 记录要插入的数据  
            int tmp = arr[i];  
            // 从已经排序的序列最右边的开始比较，找到比其小的数  
            int j = i;  
            while (j > 0 && tmp < arr[j - 1]) {  
                arr[j] = arr[j - 1];  
                j--;  
            }  
            // 存在比其小的数，插入  
            if (j != i) {  
                arr[j] = tmp;  
            }  
        }  
        return arr;

4. 快速排序

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

具体步骤：

• 从数列中挑出一个元素，称为 “基准”（pivot）;
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序

代码实现：

    public static void quickSort(int[] a, int left, int right)  {
        if(left >= right)   return;
        int i = left - 1, j = right + 1, x = a[(left + right) / 2];
        while(i < j) {
            do i++;while(a[i] < x);
            do j--;while(a[j] > x);
            if(i < j) {
                int temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
        }
        quickSort(a, left, j);
        quickSort(a, j + 1, right);
    }

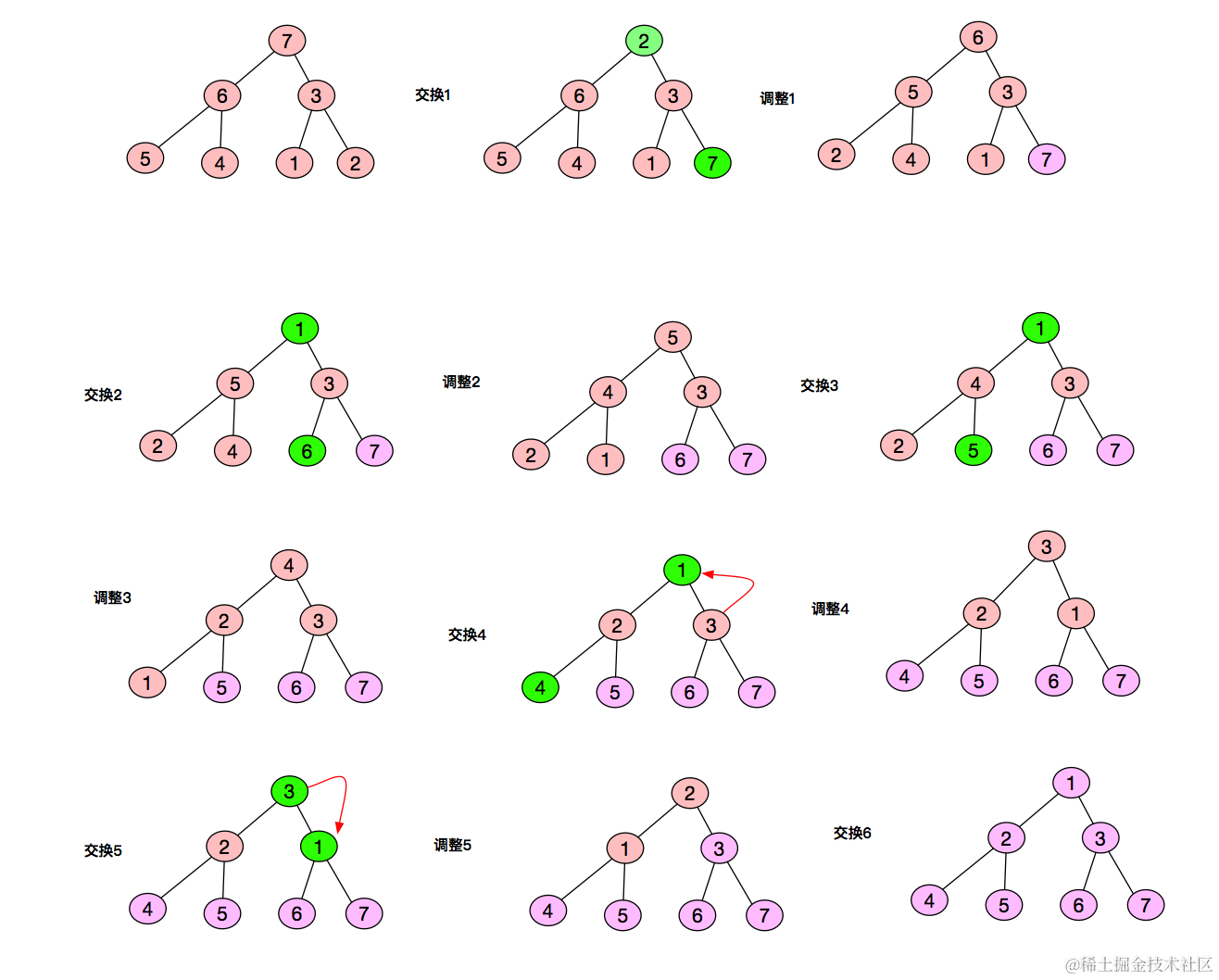
5.堆排序

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：即子结点的值总是小于（或者大于）它的父节点

具体步骤：

1. 将初始待排序列 (R1, R2, ……, Rn) 构建成大顶堆，此堆为初始的无序区；
2. 将堆顶元素 R[1] 与最后一个元素 R[n] 交换，此时得到新的无序区 (R1, R2, ……, Rn-1) 和新的有序区 (Rn), 且满足 R[1, 2, ……, n-1]<=R[n]；
3. 由于交换后新的堆顶 R[1] 可能违反堆的性质，因此需要对当前无序区 (R1, R2, ……, Rn-1) 调整为新堆，然后再次将 R [1] 与无序区最后一个元素交换，得到新的无序区 (R1, R2, ……, Rn-2) 和新的有序区 (Rn-1, Rn)。不断重复此过程直到有序区的元素个数为 n-1，则整个排序过程完成。

代码实现：

// Global variable that records the length of an array;
static int heapLen;

/**
 * Swap the two elements of an array
 * @param arr
 * @param i
 * @param j
 */
private static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

/**
 * Build Max Heap
 * @param arr
 */
private static void buildMaxHeap(int[] arr) {
    for (int i = arr.length / 2 - 1; i >= 0; i--) {
        heapify(arr, i);
    }
}

/**
 * Adjust it to the maximum heap
 * @param arr
 * @param i
 */
private static void heapify(int[] arr, int i) {
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int largest = i;
    if (right < heapLen && arr[right] > arr[largest]) {
        largest = right;
    }
    if (left < heapLen && arr[left] > arr[largest]) {
        largest = left;
    }
    if (largest != i) {
        swap(arr, largest, i);
        heapify(arr, largest);
    }
}

/**
 * Heap Sort
 * @param arr
 * @return
 */
public static int[] heapSort(int[] arr) {
    // index at the end of the heap
    heapLen = arr.length;
    // build MaxHeap
    buildMaxHeap(arr);
    for (int i = arr.length - 1; i > 0; i--) {
        // Move the top of the heap to the tail of the heap in turn
        swap(arr, 0, i);
        heapLen -= 1;
        heapify(arr, 0);
    }
    return arr;
}

习题：

1. 将整数数组（7-6-5-3-4-1-2）按照堆的排序原地进行升序排列，请问在整个排序过程中，元素3的数组下标发生过___次改变

答案：3

3. 将整数数组（7-6-3-5-4-1-2）按照堆的排序原地进行升序排列，请问在整个排序过程中，元素3的数组下标发生过___次改变

答案：2

先写这五种，后面的等有空的时候进行补充