excel统计分析——K-S正态性检验

发布时间：2023年12月25日

参考资料：

马兴华,张晋昕.数值变量正态性检验常用方法的对比[J].循证医学,2014,14(02):123-128

统计推断——正态性检验（图形方法、偏度和峰度、统计（拟合优度）检验）_sm.distributions.ecdf-CSDN博客

K-S检验法判断数据分布类型_ks检验-CSDN博客

https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/kolmogorov-smirnov-test/

https://real-statistics.com/statistics-tables/kolmogorov-smirnov-table/

https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/kolmogorov-smirnov-test/kolmogorov-distribution/

? ? ? ?K-S检验法（Kolmogorov-Smirnov test，柯尔莫哥罗夫-斯米尔诺夫检验）是一种非参数检验方法，用于检验一个样本是否来自特定的概率分布（one-sample K-S test），或者检验两个样本是否来自同一概率分布（two-sample K-S test）。

? ? ? ?K-S检验是大样本下更容易成功接受正态性假设的一种检验方法，统计软件SPSS规定样本含量大于5000时，以K-S检验结果为准；而统计软件SAS规定样本含量大于2000时以K-S检验结果为准。

K-S检验是一种基于经验分布函数的检验方法。具体如下：

1、假设总体分布函数F(x)未知，但有n个样本观测值，则把样本中n个观测值按从小到大的次序排列为x1≤x2≤...≤xn，可以得到经验分布函数如下：

F_{n}(x)=0, x< x_{1}

F_{n}(x)=i/n,x_{i }\leqslant x< x_{i+1},i=1,2,...,n-1

F_{n}(x)=1,x\geqslant x_{n}

2、根据Glivenko-Cantelli定理，当n很大时，由样本观测得到的经验分布函数F_{n}(x)是总体分布函数F(x)的良好近似。

3、计算检验统计量：

D_{n}=\underset{x}{sup}\left | F(x)-F_{n}(x) \right |

D_{n}=\underset{1\leqslant i\leqslant n}{max}\left \{\left | F(x_{i})-F_{n}(x_{i}) \right | , \left | F(x_{i+1})-F_{n}(x_{i}) \right | \right \}

? ? ? ? sup函数表示一组距离中的上确界，这是个数学概念，表示在原假设Fn(x)=F(x)的条件下，Fn(x)?F(x)的绝对值的最小上界。其意图在于如果原假设成立，则Dn应该很小，如果很大，则原假设不成立。

4、计算统计量临界值：

Kolmogorov的分布函数可表示为：

F(x)=\frac{\sqrt{2\pi}}{x}\sum_{k=1}^{\infty }e^{-(2k-1)^{2}\pi^{2}/(8x^{2})}

如果n足够大，\sqrt{n}D_{n,\alpha}基本服从Kolmogorov分布。

对于任意大小的n，临界值D_{n,\alpha}的计算公式可表示为：D_{n,\alpha}=\frac{D_\alpha}{\sqrt{n}+0.12+0.11/\sqrt{n}}

D_\alpha是Kolmogorov分布的临界值，计算方式如下：

? ? ? 若α=0.05，则取1-α即0.95下的F(x)的逆函数得到Dα

由于excel中暂未内置相关函数，故直接采用查表方式查看D_{n,\alpha}临界值：

5、计算置信区间：

1-\alpha=P(D_{n}-D_{n,\alpha}) =P(\underset{x}{max}\left | F(x)-F_{n}(x) \right |\leqslant D_{n,\alpha}) =P(F_{n}(x)-D_{n,\alpha}\leqslant F(x)\leqslant F_{n}(x)+D_{n,\alpha} \, for\, all\,x)=P(\left | F(x)-F_{n}(x) \right |\leqslant D_{n,\alpha}\,for\,all\,x)

如此，F(x)的置信区间就是F_{n}(x)\pm D_{n,\alpha}。

excel操作步骤如下：

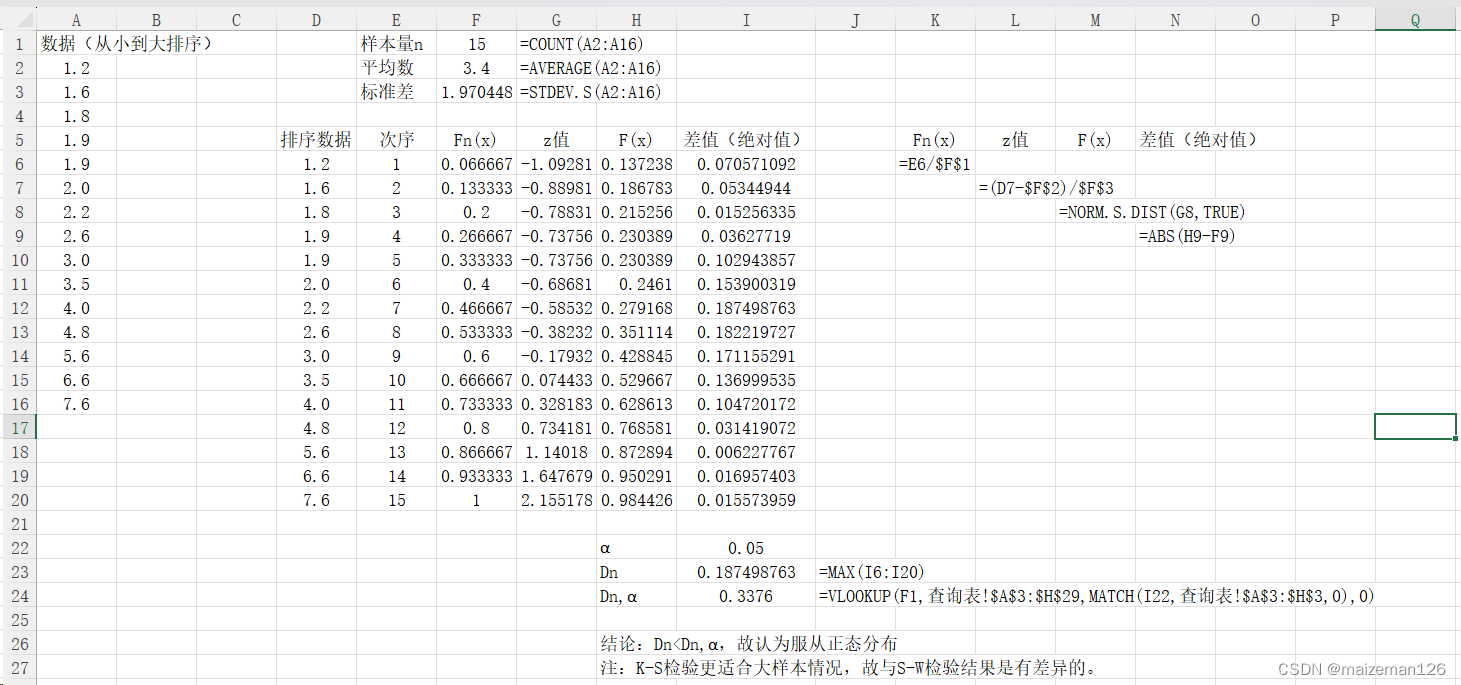
文章来源:https://blog.csdn.net/maizeman126/article/details/135196211
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章