python解决如何判断平衡二叉树问题

对于二叉树中的特殊二叉树，平衡二叉树，要想解决判断二叉树是否是平衡二叉树问题，首先需要知道什么事平衡二叉树。

平衡二叉树的概念是指给定一颗二叉树，这颗二叉树以及二叉树的所有子二叉树的左右子树的高度之差不大于1，则这棵二叉树便是平衡二叉树。

对于如何判断是否是平衡二叉树，可以使用两种方法来进行判断，一种方法是使用自顶向下的方法，另一种是采用自下而上的方法，对于这两种方法都进行一个详细的讲解。

添加图片注释，不超过 140 字（可选）

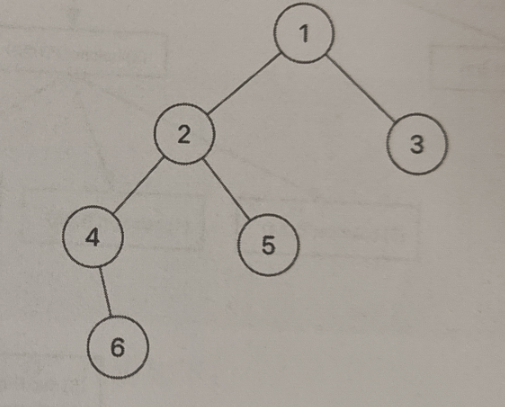
添加图片注释，不超过 140 字（可选）

以上给定的两个二叉树，第一个是平衡二叉树，第二个不是平衡二叉树。

首先是自顶向下的方法，这里会使用到求二叉树的最大深度来进行辅助判断；对于平衡二叉树，它的左右子树的高度之差不大于1，同时还保证这颗二叉树的所有子树都是平衡二叉树，也就可以保证这颗二叉树本身使平衡二叉树，使用求最大深度的方式来直接判断左右子树的高度之差。

该方法的实现主要是将二叉树的根节点root传入主调函数中，主调函数的终止条件是如果该节点为空节点，即结束并且返回的是该二叉数是平衡二叉树的结果，而如果该节点不是空，则会有三个判断并集，分别是判断左子树是否是平衡二叉树、右子树是否是平衡二叉树、节点的左右子树高度差是否小于等于1。代码实现如下：

def balance(root):
    if not root:
        return True
    return balance(root.left) and balance(root.right) and abs(maxDepth(root.left)-maxDepth(root.right))<=1
def maxDepth(root):
    if root:
        return 0
    else:
        return max(maxDepth(root.left),maxDepth(root.right))+1

对如上的方法可以看出，整个过程还是较为简洁明了的，但是能够看出这里面有很多的重复运算，而且随着数据量的提升，问题规模逐渐增大，则整个过程中的重复计算会越来越多，就会导致效率的逐渐降低。下图中可以看到maxDepth函数执行了多次。

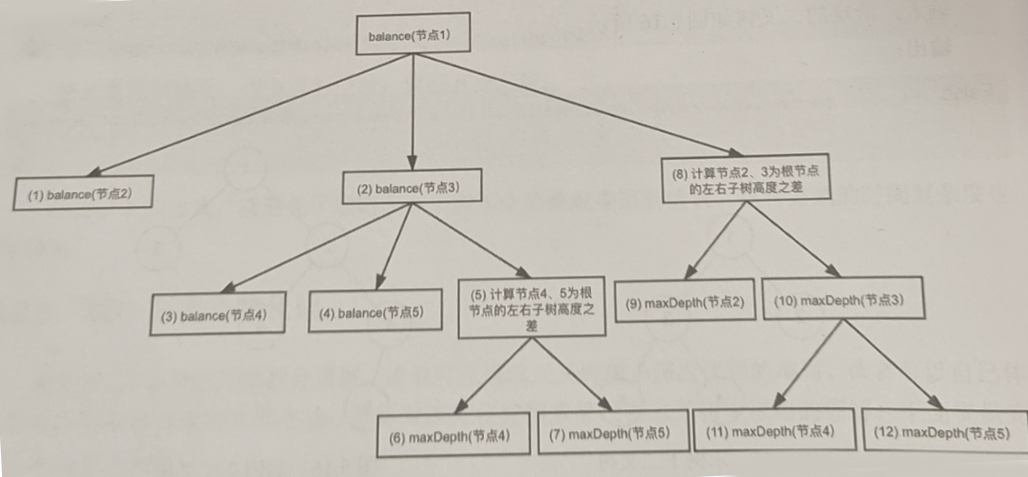
添加图片注释，不超过 140 字（可选）

针对自上而下的重复计算，可以使用自下而上的方式啦进行优化，对于每一棵树，如果计算左子树和右子树的高度的时候，当发现做优子树的高度差不大于1的时候，就向上层返回左右子树的最大高度值加一，而当发现任何一颗子树是不平衡的子树的时候，就向上层返回-1，这样可以避免重复运算，使因为可以通过返回-1的方式来及时的反映出子树已经是不平衡子树了，那给定的树就不可能是平衡树了，直接终止继续计算。其python代码实现如下：

def balance(root):
    if dfs(root)==-1:
        return False
    return True
def dfs(root):
    if not root:
        return 0
    left=dfs(root.left)
    if left==-1:
        return -1
    right=dfs(root.right)
    if right==-1:
        return -1
    return max(left,right)+1 if abs(left - right) < 2 else -1