代码随想录算法训练DAY18|二叉树5
算法训练DAY18|二叉树5
513.找树左下角的值
给定一个二叉树,在树的最后一行找到最左边的值。
示例 1:

示例 2:

思路
本题要找出树的最后一行的最左边的值。此时大家应该想起用层序遍历是非常简单的了,反而用递归的话会比较难一点。
我们依然还是先介绍递归法。
#递归
咋眼一看,这道题目用递归的话就就一直向左遍历,最后一个就是答案呗?
没有这么简单,一直向左遍历到最后一个,它未必是最后一行啊。
我们来分析一下题目:在树的最后一行找到最左边的值。
首先要是最后一行,然后是最左边的值。
如果使用递归法,如何判断是最后一行呢,其实就是深度最大的叶子节点一定是最后一行。
如果对二叉树深度和高度还有点疑惑的话,请看:110.平衡二叉树 (opens new window)。
所以要找深度最大的叶子节点。
那么如何找最左边的呢?可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
递归三部曲:
-
确定递归函数的参数和返回值
参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为void。
本题还需要类里的两个全局变量,maxLen用来记录最大深度,result记录最大深度最左节点的数值。
代码如下:
int maxDepth = INT_MIN; ? // 全局变量 记录最大深度 int result; ? ? ? // 全局变量 最大深度最左节点的数值 void traversal(TreeNode* root, int depth)
-
确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
代码如下:
if (root->left == NULL && root->right == NULL) {
? ?if (depth > maxDepth) {
? ? ? ?maxDepth = depth; ? ? ? ? ? // 更新最大深度
? ? ? ?result = root->val; ? // 最大深度最左面的数值
? }
? ?return;
}
-
确定单层递归的逻辑
在找最大深度的时候,递归的过程中依然要使用回溯,代码如下:
? ? ? ? ? ? ? ? ? ?// 中
if (root->left) { ? // 左
? ?depth++; // 深度加一
? ?traversal(root->left, depth);
? ?depth--; // 回溯,深度减一
}
if (root->right) { // 右
? ?depth++; // 深度加一
? ?traversal(root->right, depth);
? ?depth--; // 回溯,深度减一
}
return;
完整代码如下:
class Solution {
public:
? ?int maxDepth = INT_MIN;
? ?int result;
? ?void traversal(TreeNode* root, int depth) {
? ? ? ?if (root->left == NULL && root->right == NULL) {
? ? ? ? ? ?if (depth > maxDepth) {
? ? ? ? ? ? ? ?maxDepth = depth;
? ? ? ? ? ? ? ?result = root->val;
? ? ? ? ? }
? ? ? ? ? ?return;
? ? ? }
? ? ? ?if (root->left) {
? ? ? ? ? ?depth++;
? ? ? ? ? ?traversal(root->left, depth);
? ? ? ? ? ?depth--; // 回溯
? ? ? }
? ? ? ?if (root->right) {
? ? ? ? ? ?depth++;
? ? ? ? ? ?traversal(root->right, depth);
? ? ? ? ? ?depth--; // 回溯
? ? ? }
? ? ? ?return;
? }
? ?int findBottomLeftValue(TreeNode* root) {
? ? ? ?traversal(root, 0);
? ? ? ?return result;
? }
};
当然回溯的地方可以精简,精简代码如下:
class Solution {
public:
? ?int maxDepth = INT_MIN;
? ?int result;
? ?void traversal(TreeNode* root, int depth) {
? ? ? ?if (root->left == NULL && root->right == NULL) {
? ? ? ? ? ?if (depth > maxDepth) {
? ? ? ? ? ? ? ?maxDepth = depth;
? ? ? ? ? ? ? ?result = root->val;
? ? ? ? ? }
? ? ? ? ? ?return;
? ? ? }
? ? ? ?if (root->left) {
? ? ? ? ? ?traversal(root->left, depth + 1); // 隐藏着回溯
? ? ? }
? ? ? ?if (root->right) {
? ? ? ? ? ?traversal(root->right, depth + 1); // 隐藏着回溯
? ? ? }
? ? ? ?return;
? }
? ?int findBottomLeftValue(TreeNode* root) {
? ? ? ?traversal(root, 0);
? ? ? ?return result;
? }
};
如果对回溯部分精简的代码 不理解的话,可以看这篇257. 二叉树的所有路径(opens new window)
#迭代法
本题使用层序遍历再合适不过了,比递归要好理解得多!
只需要记录最后一行第一个节点的数值就可以了。
如果对层序遍历不了解,看这篇二叉树:层序遍历登场! (opens new window),这篇里也给出了层序遍历的模板,稍作修改就一过刷了这道题了。
代码如下:
class Solution {
public:
? ?int findBottomLeftValue(TreeNode* root) {
? ? ? ?queue<TreeNode*> que;
? ? ? ?if (root != NULL) que.push(root);
? ? ? ?int result = 0;
? ? ? ?while (!que.empty()) {
? ? ? ? ? ?int size = que.size();
? ? ? ? ? ?for (int i = 0; i < size; i++) {
? ? ? ? ? ? ? ?TreeNode* node = que.front();
? ? ? ? ? ? ? ?que.pop();
? ? ? ? ? ? ? ?if (i == 0) result = node->val; // 记录最后一行第一个元素
? ? ? ? ? ? ? ?if (node->left) que.push(node->left);
? ? ? ? ? ? ? ?if (node->right) que.push(node->right);
? ? ? ? ? }
? ? ? }
? ? ? ?return result;
? }
};
#总结
本题涉及如下几点:
-
递归求深度的写法,我们在110.平衡二叉树?中详细的分析了深度应该怎么求,高度应该怎么求。
-
递归中其实隐藏了回溯,在257. 二叉树的所有路径?中讲解了究竟哪里使用了回溯,哪里隐藏了回溯。
-
层次遍历,在二叉树:层序遍历登场!?深度讲解了二叉树层次遍历。 所以本题涉及到的点,我们之前都讲解过,这些知识点需要同学们灵活运用,这样就举一反三了。
###
112. 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
思路
相信很多同学都会疑惑,递归函数什么时候要有返回值,什么时候没有返回值,特别是有的时候递归函数返回类型为bool类型。
那么接下来我通过详细讲解如下两道题,来回答这个问题:
这道题我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。
#递归
可以使用深度优先遍历的方式(本题前中后序都可以,无所谓,因为中节点也没有处理逻辑)来遍历二叉树
-
确定递归函数的参数和返回类型
参数:需要二叉树的根节点,还需要一个计数器,这个计数器用来计算二叉树的一条边之和是否正好是目标和,计数器为int型。
再来看返回值,递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
-
如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(这种情况就是本文下半部分介绍的113.路径总和ii)
-
如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (这种情况我们在236. 二叉树的最近公共祖先?中介绍)
-
如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(本题的情况)
而本题我们要找一条符合条件的路径,所以递归函数需要返回值,及时返回,那么返回类型是什么呢?
如图所示:
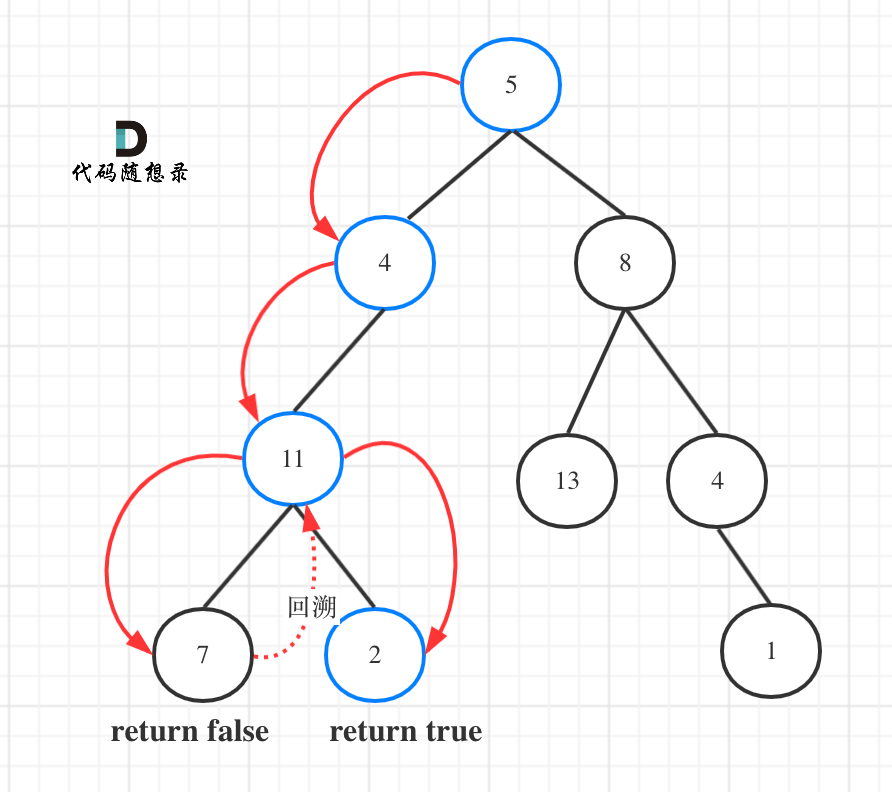
图中可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。
所以代码如下:
bool traversal(treenode* cur, int count) ? // 注意函数的返回类型
-
确定终止条件
首先计数器如何统计这一条路径的和呢?
不要去累加然后判断是否等于目标和,那么代码比较麻烦,可以用递减,让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
如果最后count == 0,同时到了叶子节点的话,说明找到了目标和。
如果遍历到了叶子节点,count不为0,就是没找到。
递归终止条件代码如下:
if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点,并且计数为0 if (!cur->left && !cur->right) return false; // 遇到叶子节点而没有找到合适的边,直接返回
-
确定单层递归的逻辑
因为终止条件是判断叶子节点,所以递归的过程中就不要让空节点进入递归了。
递归函数是有返回值的,如果递归函数返回true,说明找到了合适的路径,应该立刻返回。
代码如下:
if (cur->left) { // 左 (空节点不遍历)
? ?// 遇到叶子节点返回true,则直接返回true
? ?if (traversal(cur->left, count - cur->left->val)) return true; // 注意这里有回溯的逻辑
}
if (cur->right) { // 右 (空节点不遍历)
? ?// 遇到叶子节点返回true,则直接返回true
? ?if (traversal(cur->right, count - cur->right->val)) return true; // 注意这里有回溯的逻辑
}
return false;
以上代码中是包含着回溯的,没有回溯,如何后撤重新找另一条路径呢。
回溯隐藏在traversal(cur->left, count - cur->left->val)这里, 因为把count - cur->left->val 直接作为参数传进去,函数结束,count的数值没有改变。
为了把回溯的过程体现出来,可以改为如下代码:
if (cur->left) { // 左
? ?count -= cur->left->val; // 递归,处理节点;
? ?if (traversal(cur->left, count)) return true;
? ?count += cur->left->val; // 回溯,撤销处理结果
}
if (cur->right) { // 右
? ?count -= cur->right->val;
? ?if (traversal(cur->right, count)) return true;
? ?count += cur->right->val;
}
return false;
整体代码如下:
class Solution {
private:
? ?bool traversal(TreeNode* cur, int count) {
? ? ? ?if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点,并且计数为0
? ? ? ?if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回
?
? ? ? ?if (cur->left) { // 左
? ? ? ? ? ?count -= cur->left->val; // 递归,处理节点;
? ? ? ? ? ?if (traversal(cur->left, count)) return true;
? ? ? ? ? ?count += cur->left->val; // 回溯,撤销处理结果
? ? ? }
? ? ? ?if (cur->right) { // 右
? ? ? ? ? ?count -= cur->right->val; // 递归,处理节点;
? ? ? ? ? ?if (traversal(cur->right, count)) return true;
? ? ? ? ? ?count += cur->right->val; // 回溯,撤销处理结果
? ? ? }
? ? ? ?return false;
? }
?
public:
? ?bool hasPathSum(TreeNode* root, int sum) {
? ? ? ?if (root == NULL) return false;
? ? ? ?return traversal(root, sum - root->val);
? }
};
以上代码精简之后如下:
class Solution {
public:
? ?bool hasPathSum(TreeNode* root, int sum) {
? ? ? ?if (!root) return false;
? ? ? ?if (!root->left && !root->right && sum == root->val) {
? ? ? ? ? ?return true;
? ? ? }
? ? ? ?return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
? }
};
自己提交版
class Solution {
private:
? ?bool searchPath(TreeNode* node,int count){
? ? ? ?if(node==nullptr) return false;
? ? ? ?count -= node->val;
? ? ? ?if(node->left==nullptr&&node->right==nullptr&&count==0) return true;
? ? ? ?if(node->left==nullptr&&node->right==nullptr&&count!=0) return false;
? ? ? ?bool left=false,right=false;
? ? ? ?if(node->left) left = searchPath(node->left,count);
? ? ? ?if(node->right) right = searchPath(node->right,count);
? ? ? ?return left||right;
? }
public:
? ?bool hasPathSum(TreeNode* root, int targetSum) {
? ? ? ?
? ? ? ?return searchPath(root,targetSum);
? }
};
#迭代
跳过
113. 路径总和ii
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树,以及目标和 sum = 22,

#思路
113.路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值!
如图:

为了尽可能的把细节体现出来,我写出如下代码(这份代码并不简洁,但是逻辑非常清晰)
class solution {
private:
? ?vector<vector<int>> result;
? ?vector<int> path;
? ?// 递归函数不需要返回值,因为我们要遍历整个树
? ?void traversal(TreeNode* cur, int count) {
? ? ? ?if (!cur->left && !cur->right && count == 0) { // 遇到了叶子节点且找到了和为sum的路径
? ? ? ? ? ?result.push_back(path);
? ? ? ? ? ?return;
? ? ? }
?
? ? ? ?if (!cur->left && !cur->right) return ; // 遇到叶子节点而没有找到合适的边,直接返回
?
? ? ? ?if (cur->left) { // 左 (空节点不遍历)
? ? ? ? ? ?path.push_back(cur->left->val);
? ? ? ? ? ?count -= cur->left->val;
? ? ? ? ? ?traversal(cur->left, count); ? ?// 递归
? ? ? ? ? ?count += cur->left->val; ? ? ? ?// 回溯
? ? ? ? ? ?path.pop_back(); ? ? ? ? ? ? ? ?// 回溯
? ? ? }
? ? ? ?if (cur->right) { // 右 (空节点不遍历)
? ? ? ? ? ?path.push_back(cur->right->val);
? ? ? ? ? ?count -= cur->right->val;
? ? ? ? ? ?traversal(cur->right, count); ? // 递归
? ? ? ? ? ?count += cur->right->val; ? ? ? // 回溯
? ? ? ? ? ?path.pop_back(); ? ? ? ? ? ? ? ?// 回溯
? ? ? }
? ? ? ?return ;
? }
?
public:
? ?vector<vector<int>> pathSum(TreeNode* root, int sum) {
? ? ? ?result.clear();
? ? ? ?path.clear();
? ? ? ?if (root == NULL) return result;
? ? ? ?path.push_back(root->val); // 把根节点放进路径
? ? ? ?traversal(root, sum - root->val);
? ? ? ?return result;
? }
};
至于113. 路径总和ii 的迭代法我并没有写,用迭代方式记录所有路径比较麻烦,也没有必要,如果大家感兴趣的话,可以再深入研究研究。
#总结
本篇通过leetcode上112. 路径总和 和 113. 路径总和ii 详细的讲解了 递归函数什么时候需要返回值,什么不需要返回值。
这两道题目是掌握这一知识点非常好的题目,大家看完本篇文章再去做题,就会感受到搜索整棵树和搜索某一路径的差别。
对于112. 路径总和,我依然给出了递归法和迭代法,这种题目其实用迭代法会复杂一些,能掌握递归方式就够了!
自己提交版
class Solution {
public:
? ?vector<vector<int>> result;
? ?vector<int> path;
? ?void serchPath(TreeNode* node,int count,vector<int> path){
? ? ? ?if(node==nullptr) return;
? ? ? ?path.push_back(node->val);
? ? ? ?count-=node->val;
? ? ? ?if(node->left==nullptr&&node->right==nullptr&&count==0){
? ? ? ? ? ?result.push_back(path);
? ? ? ? ? ?return;
? ? ? }
? ? ? ?if(node->left) serchPath(node->left,count,path);
? ? ? ?if(node->right) serchPath(node->right,count,path);
? ?
? }
?
? ?vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
? ? ? ?serchPath(root,targetSum,path);
? ? ? ?return result;
? }
};
106.从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
-
中序遍历 inorder = [9,3,15,20,7]
-
后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树:

思路
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:

那么代码应该怎么写呢?
说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
-
第一步:如果数组大小为零的话,说明是空节点了。
-
第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
-
第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
-
第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
-
第五步:切割后序数组,切成后序左数组和后序右数组
-
第六步:递归处理左区间和右区间
不难写出如下代码:(先把框架写出来)
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
?
? ?// 第一步
? ?if (postorder.size() == 0) return NULL;
?
? ?// 第二步:后序遍历数组最后一个元素,就是当前的中间节点
? ?int rootValue = postorder[postorder.size() - 1];
? ?TreeNode* root = new TreeNode(rootValue);
?
? ?// 叶子节点
? ?if (postorder.size() == 1) return root;
?
? ?// 第三步:找切割点
? ?int delimiterIndex;
? ?for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
? ? ? ?if (inorder[delimiterIndex] == rootValue) break;
? }
?
? ?// 第四步:切割中序数组,得到 中序左数组和中序右数组
? ?// 第五步:切割后序数组,得到 后序左数组和后序右数组
?
? ?// 第六步
? ?root->left = traversal(中序左数组, 后序左数组);
? ?root->right = traversal(中序右数组, 后序右数组);
?
? ?return root;
}
此时应该注意确定切割的标准,是左闭右开,还有左开右闭,还是左闭右闭,这个就是不变量,要在递归中保持这个不变量。
在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭右闭,必然乱套!
首先要切割中序数组,为什么先切割中序数组呢?
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
// 找到中序遍历的切割点
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
? ?if (inorder[delimiterIndex] == rootValue) break;
}
?
// 左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
接下来就要切割后序数组了。
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
后序数组的切割点怎么找?
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
代码如下:
// postorder 舍弃末尾元素,因为这个元素就是中间节点,已经用过了 postorder.resize(postorder.size() - 1); ? // 左闭右开,注意这里使用了左中序数组大小作为切割点:[0, leftInorder.size) vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size()); // [leftInorder.size(), end) vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
此时,中序数组切成了左中序数组和右中序数组,后序数组切割成左后序数组和右后序数组。
接下来可以递归了,代码如下:
root->left = traversal(leftInorder, leftPostorder); root->right = traversal(rightInorder, rightPostorder);
完整代码如下:
class Solution {
private:
? ?TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
? ? ? ?if (postorder.size() == 0) return NULL;
?
? ? ? ?// 后序遍历数组最后一个元素,就是当前的中间节点
? ? ? ?int rootValue = postorder[postorder.size() - 1];
? ? ? ?TreeNode* root = new TreeNode(rootValue);
?
? ? ? ?// 叶子节点
? ? ? ?if (postorder.size() == 1) return root;
?
? ? ? ?// 找到中序遍历的切割点
? ? ? ?int delimiterIndex;
? ? ? ?for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
? ? ? ? ? ?if (inorder[delimiterIndex] == rootValue) break;
? ? ? }
?
? ? ? ?// 切割中序数组
? ? ? ?// 左闭右开区间:[0, delimiterIndex)
? ? ? ?vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
? ? ? ?// [delimiterIndex + 1, end)
? ? ? ?vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
?
? ? ? ?// postorder 舍弃末尾元素
? ? ? ?postorder.resize(postorder.size() - 1);
?
? ? ? ?// 切割后序数组
? ? ? ?// 依然左闭右开,注意这里使用了左中序数组大小作为切割点
? ? ? ?// [0, leftInorder.size)
? ? ? ?vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
? ? ? ?// [leftInorder.size(), end)
? ? ? ?vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
?
? ? ? ?root->left = traversal(leftInorder, leftPostorder);
? ? ? ?root->right = traversal(rightInorder, rightPostorder);
?
? ? ? ?return root;
? }
public:
? ?TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
? ? ? ?if (inorder.size() == 0 || postorder.size() == 0) return NULL;
? ? ? ?return traversal(inorder, postorder);
? }
};
此时应该发现了,如上的代码性能并不好,因为每层递归定义了新的vector(就是数组),既耗时又耗空间,但上面的代码是最好理解的,为了方便读者理解,所以用如上的代码来讲解。
下面给出用下标索引写出的代码版本:(思路是一样的,只不过不用重复定义vector了,每次用下标索引来分割)
class Solution {
private:
? ?// 中序区间:[inorderBegin, inorderEnd),后序区间[postorderBegin, postorderEnd)
? ?TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
? ? ? ?if (postorderBegin == postorderEnd) return NULL;
?
? ? ? ?int rootValue = postorder[postorderEnd - 1];
? ? ? ?TreeNode* root = new TreeNode(rootValue);
?
? ? ? ?if (postorderEnd - postorderBegin == 1) return root;
?
? ? ? ?int delimiterIndex;
? ? ? ?for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
? ? ? ? ? ?if (inorder[delimiterIndex] == rootValue) break;
? ? ? }
? ? ? ?// 切割中序数组
? ? ? ?// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
? ? ? ?int leftInorderBegin = inorderBegin;
? ? ? ?int leftInorderEnd = delimiterIndex;
? ? ? ?// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
? ? ? ?int rightInorderBegin = delimiterIndex + 1;
? ? ? ?int rightInorderEnd = inorderEnd;
?
? ? ? ?// 切割后序数组
? ? ? ?// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
? ? ? ?int leftPostorderBegin = ?postorderBegin;
? ? ? ?int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
? ? ? ?// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
? ? ? ?int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
? ? ? ?int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
?
? ? ? ?root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, ?postorder, leftPostorderBegin, leftPostorderEnd);
? ? ? ?root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
?
? ? ? ?return root;
? }
public:
? ?TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
? ? ? ?if (inorder.size() == 0 || postorder.size() == 0) return NULL;
? ? ? ?// 左闭右开的原则
? ? ? ?return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
? }
};
105.从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树:

105.从前序与中序遍历序列构造二叉树,最后版本,C++代码:
class Solution {
private:
? ? ? ?TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
? ? ? ?if (preorderBegin == preorderEnd) return NULL;
?
? ? ? ?int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
? ? ? ?TreeNode* root = new TreeNode(rootValue);
?
? ? ? ?if (preorderEnd - preorderBegin == 1) return root;
?
? ? ? ?int delimiterIndex;
? ? ? ?for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
? ? ? ? ? ?if (inorder[delimiterIndex] == rootValue) break;
? ? ? }
? ? ? ?// 切割中序数组
? ? ? ?// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
? ? ? ?int leftInorderBegin = inorderBegin;
? ? ? ?int leftInorderEnd = delimiterIndex;
? ? ? ?// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
? ? ? ?int rightInorderBegin = delimiterIndex + 1;
? ? ? ?int rightInorderEnd = inorderEnd;
?
? ? ? ?// 切割前序数组
? ? ? ?// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
? ? ? ?int leftPreorderBegin = ?preorderBegin + 1;
? ? ? ?int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
? ? ? ?// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
? ? ? ?int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
? ? ? ?int rightPreorderEnd = preorderEnd;
?
? ? ? ?root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, ?preorder, leftPreorderBegin, leftPreorderEnd);
? ? ? ?root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
?
? ? ? ?return root;
? }
?
public:
? ?TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
? ? ? ?if (inorder.size() == 0 || preorder.size() == 0) return NULL;
?
? ? ? ?// 参数坚持左闭右开的原则
? ? ? ?return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
? }
};
#思考题
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
那么前序和后序可不可以唯一确定一棵二叉树呢?
前序和后序不能唯一确定一棵二叉树!,因为没有中序遍历无法确定左右部分,也就是无法分割。
举一个例子:
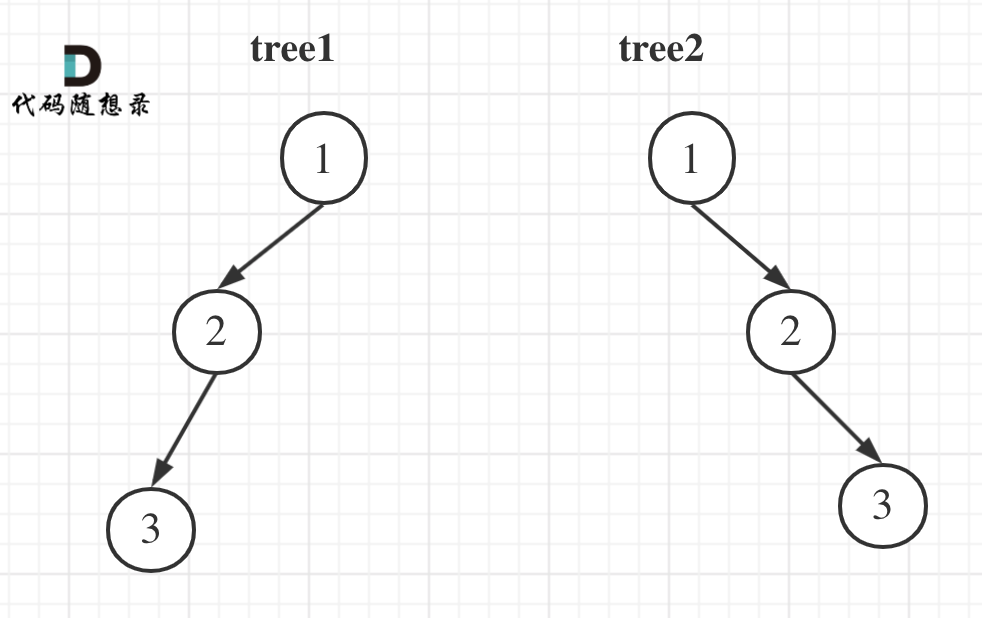
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和 tree2 的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一棵二叉树!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 第41节: Vue3 watch函数
- react自适应布局
- 一起来加深对 SASS 的理解「最强总结篇,含Demo」
- 100天精通鸿蒙从入门到跳槽——第9天:TypeScript 知识储备:命名空间
- 初识Linux
- Ansible:简单、快速、安全、最强大的 IT 自动化系统 | 开源日报 No.140
- 范仲淹:文能治盛世,武可镇山河
- UI自动化测试框架搭建 —— yaml文件管理定位元素
- 《房地产赚钱笔记:人人都该上的10堂投资课》
- 【UnityShader入门精要学习笔记】第三章(1)Unity Shader介绍