路径规划中常用的抽稀(simplification)算法

简介

? ? ? ?在路径规划中，过度密集的路径点不仅会增加计算和存储的负担，还可能导致路径冗余和效率下降，因此需要进行抽稀处理，同时保留路径的形状特征和轨迹信息，确保路径规划的精度和实时性。常见的抽稀算法有Ramer-Douglas-Peucker(RDP)算法和垂距限值法。

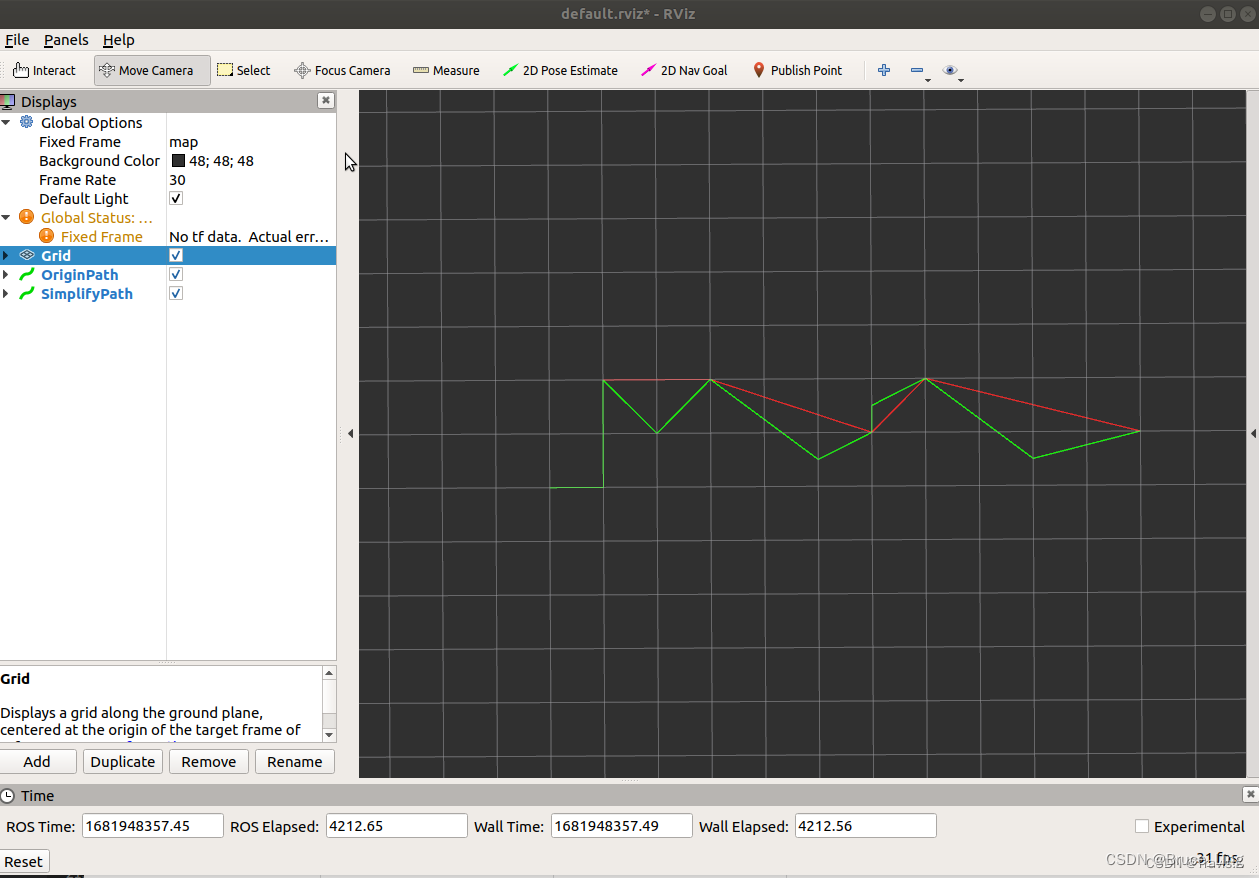
一、RDP算法

?基本原理：

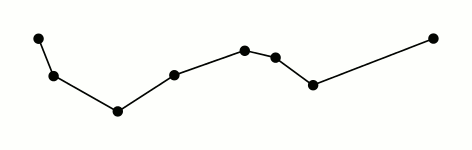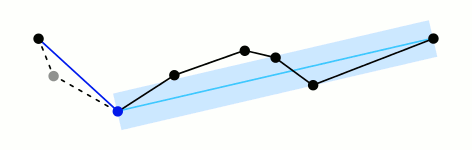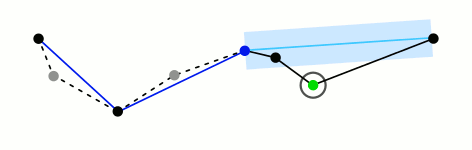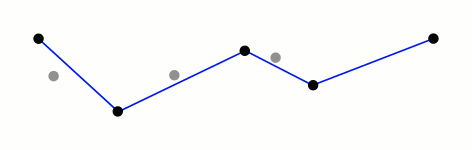
? ? ? ?RDP算法基于几何距离，选定路径的起点和终点，然后寻找路径中离这条直线距离最大的点，如果这个最大距离大于一个预定的阈值，则将这个点加入到新的路径中，同时将原路径分为两部分，递归进行此操作；如果最大距离小于阈值，则所有的中间点都可以删除。

算法步骤：?

1、已知给定的一条由n个点构成的路径。（两点之间可以是直线也可以是曲线）

2、在起点和终点之间找出垂距（点和直线的垂直距离）最大的点，如果垂距大于阈值，将路径以此点为分界点分为2部分；如果垂距小于阈值，剔除所有中间点。

3、递归步骤2.

?二、垂距限值法

?基本原理：

? ? ? ? 垂距限值法其实可以看做是一种简化版本的Ramer-Douglas-Peucker算法（RDP算法），它主要用于路径或者轨迹的抽稀，即剔除冗余点，以简化数据结构，降低计算哈比森和存储的负担。

?算法步骤：

1、已知给定的一条由n个点构成的路径。（两点之间可以是直线也可以是曲线）

2、除了起点和终点之外，计算所有点到起点和终点连成直线的垂距，如果垂距大于阈值，保留，反之，剔除。

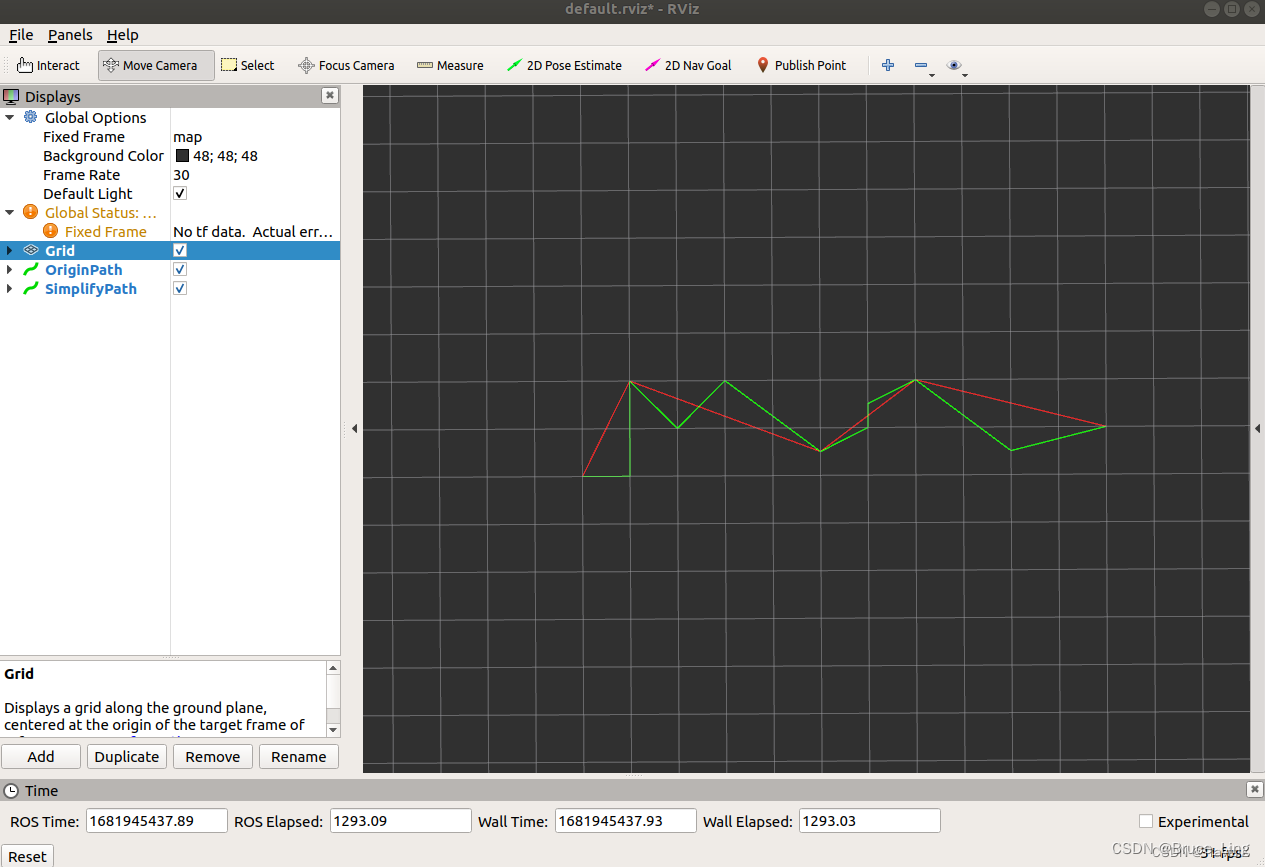
?还有一种算法是，基于每个点与上一个点和下一个点形成的直线的垂距进行抽稀。