交叉熵损失函数

前言

我们在线性回归中很好地理解了均方误差的公式。理解了要进行全局误差优化(在线性回归中通常是梯度下降)首先得有一个损失函数来计算单个数据的损失。在多分类问题解决方法Softmax回归模型中，通常使用的损失函数就是交叉熵损失函数，在讲交叉熵损失函数之前，我们先理解了Softmax函数是如何将数据转换为概率的。

概念

交叉熵误差计算的是模型预测的概率分布与实际概率分布之间的差异。对于一个多分类问题，假设模型的输出经过 Softmax 函数转换成了概率分布$P$，并且我们有真实的标签概率分布$Q$。交叉熵损失函数如下：
$$H(Q,P)=?\sum _{c=1}^C{Q}_{c}log(P_c)$$
其中：

• $C$是类别的总数。
• $Q_c$ 是真实标签的概率分布，通常是独热编码(one-hot encoded)向量，如[1, 0, 0]即表示当前类别为1或0的向量(有且只有以列为1，表示当前类别的概率为100%)。
• $P_c$ 是模型预测的概率分布，通过如 Softmax 函数的输出获得。
• 求和$\sum$是对所有类别$c$进行累加。
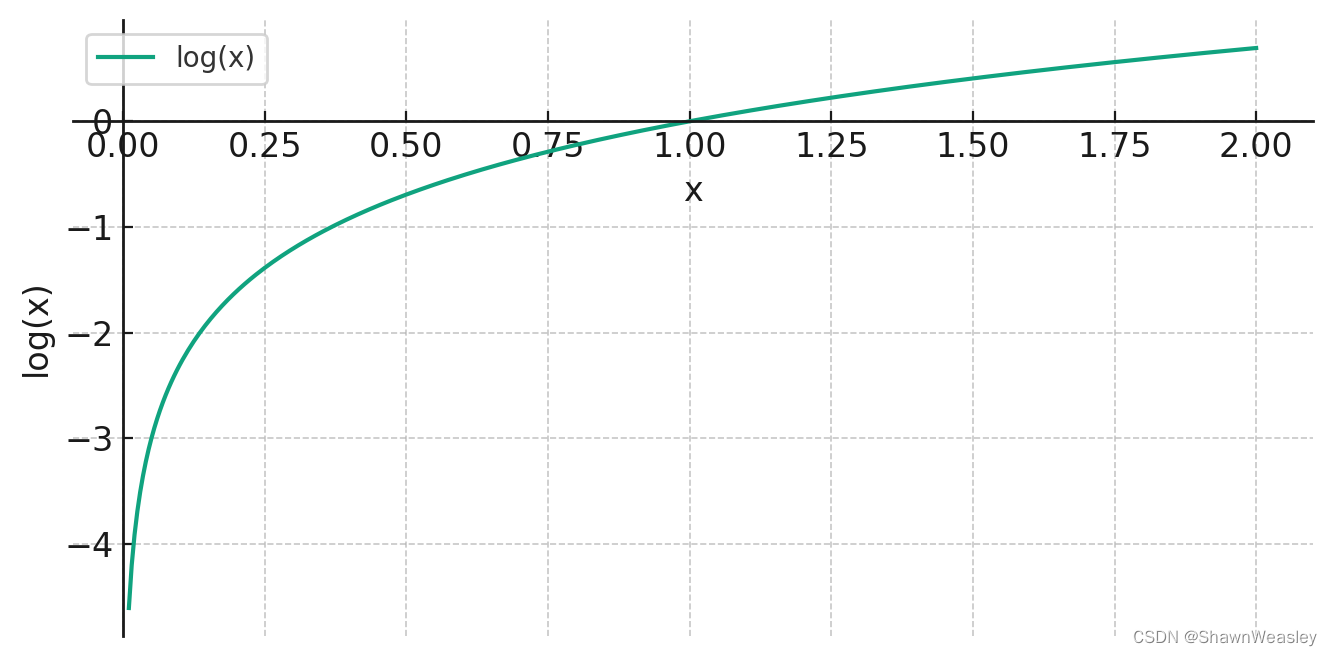
• 使用负号是因为由于$P_c$是概率值，所以它的范围在0到1之间，对数值将是负数。如下图为log的曲线，当x接近 1 时，$log(x)$接近 0，表示如果预测概率与实际发生概率相匹配，损失会变小。这种特性使得$log$函数非常适合于衡量预测概率与实际概率之间的差异。而$?log(P_c)$就可以将负数变正，最外面的负号是提取出来的。
  
  转换为$J(\theta )$表示就是：

$$J(\theta )=?\frac{1}{m}\sum _{i=1}^m\sum _{c=1}^C{y}_c^{(i)}\log (h_{\theta }(x^{(i)}{)}_c)$$
其中：

• $J(\theta )$是基于模型参数 ( \theta ) 的损失函数。
• $m$是样本的总数。
• $C$是类别的总数。
• $y_c^{(i)}$是一个指示器（indicator）变量，表示如果样本$i$属于类$c$，则$y_c^{(i)}=1$，否则$y_c^{(i)}=0$。
• $h_{\theta }(x^{(i)}{)}_c$是模型对于样本$i$属于类别$c$的预测概率。

对于二分类问题，这个公式可以简化为：

$$J(\theta )=?\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (h_{\theta }(x^{(i)}))+(1?y^{(i)})\log (1?h_{\theta }(x^{(i)}))]$$

这里：

• $y^{(i)}$是样本$i$的实际标签（0 或 1）。
• $h_{\theta }(x^{(i)})$是模型预测样本$i$为 1 的概率。

交叉熵损失现在已经被应用于非常多的方面，不仅仅是多分类问题，能够很好地衡量两个概率分布之间差异的度量。交叉熵损失函数比均方误差更不容易陷入梯度消失的问题，所以在机器学习框架中（如TensorFlow或PyTorch），交叉熵损失函数通常已经作为内置函数实现。

在代码中Softmax回归代码如下，使用鸢尾花数据集可以获得100%正确率的成绩，相比逻辑回归OvR策略的结果要好很多：

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建Softmax回归模型
softmax_reg = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)

# 训练模型
softmax_reg.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = softmax_reg.predict(X_test)

# 评估模型
report = classification_report(y_test, y_pred)

print(report)

分类结果：

类别	精度 (Precision)	召回率 (Recall)	F1得分	支持 (Support)
0	1.00	1.00	1.00	19
1	1.00	1.00	1.00	13
2	1.00	1.00	1.00	13
总计	1.00	1.00	1.00	45