（2023|ICCV，diffusion，transformer，Gflops）使用 Transformer 的可扩展扩散模型

Scalable Diffusion Models with Transformers

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

目录

0. 摘要

3. Diffusion Transformer

3.1 基础

3.2 扩散 Transformer 设计空间?

4. 实验

---

0. 摘要

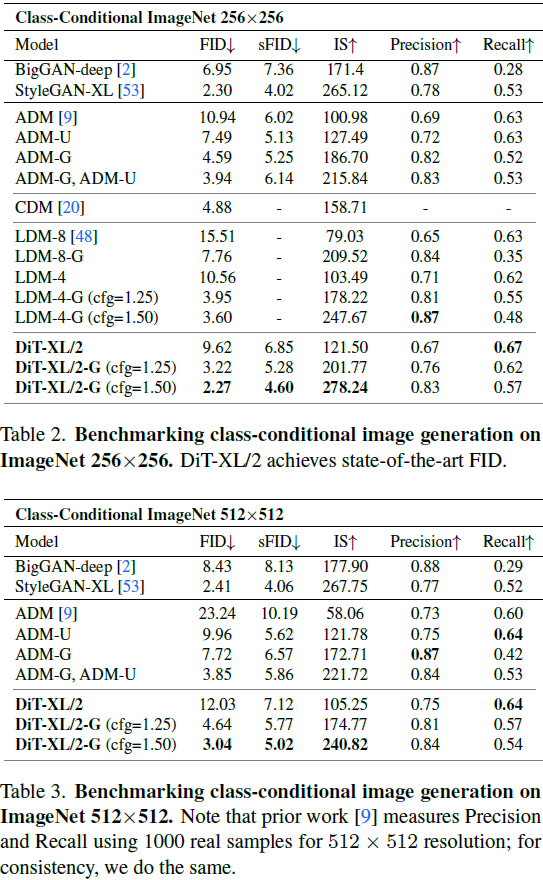
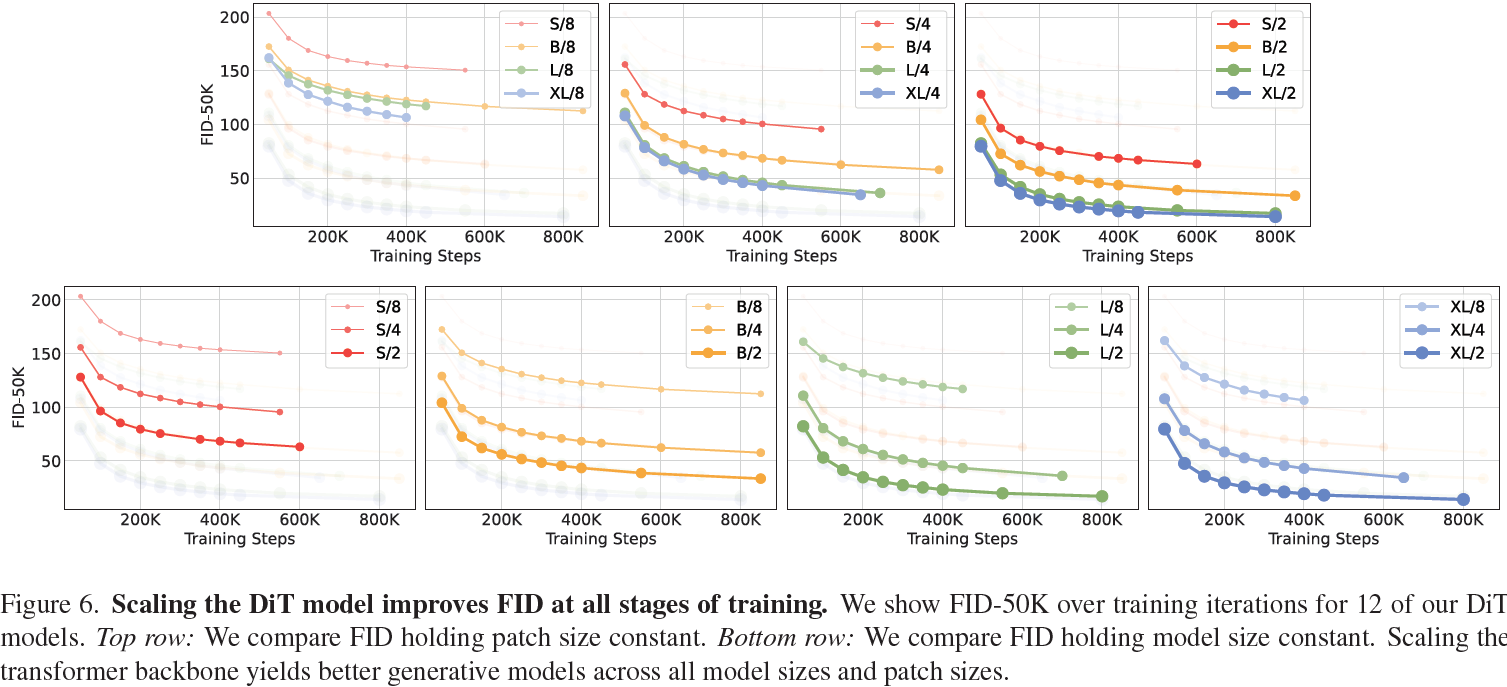
我们探索一种基于 Transformer 架构的新型扩散模型。我们训练图像的潜在扩散模型，将通常使用的 U-Net 骨干替换为在潜在 patch 上操作的 Transformer。我们通过前向传播复杂度的角度分析我们的扩散 Transformer（Diffusion Transformers，DiT）的可扩展性，该复杂度由 Gflops 测量。我们发现，具有更高 Gflops 的 DiTs（通过增加 Transformer 的深度/宽度或增加输入标记的数量）始终具有较低的 FID。除了具有良好的可扩展性特性外，我们最大的 DiT-XL/2 模型在类条件ImageNet 512x512 和 256x256 基准上优于所有先前的扩散模型，后者实现了 2.27 的最先进 FID。

3. Diffusion Transformer

3.1 基础

DDPM，无分类器引导，LDM

架构复杂性。在图像生成领域评估架构复杂性时，使用参数计数是一种相当常见的做法。总体上，参数计数可能是评估图像模型复杂性的不良代理，因为它们未考虑例如影响性能的图像分辨率等因素 [44, 45]。相反，本文中对模型复杂性的分析主要通过理论上的 Gflops 视角进行。这使我们与架构设计文献保持一致，其中 Gflops 被广泛用于衡量复杂性。在实践中，黄金复杂度度量（golden complexity metric）仍然存在争议，因为它经常取决于特定的应用场景。Nichol 和 Dhariwal 的开创性工作改进扩散模型 [9, 36] 与我们最相关——其中，他们分析了 U-Net 架构类的可扩展性和Gflop 特性。在本文中，我们专注于 Transformer 类。?

3.2 扩散 Transformer 设计空间?

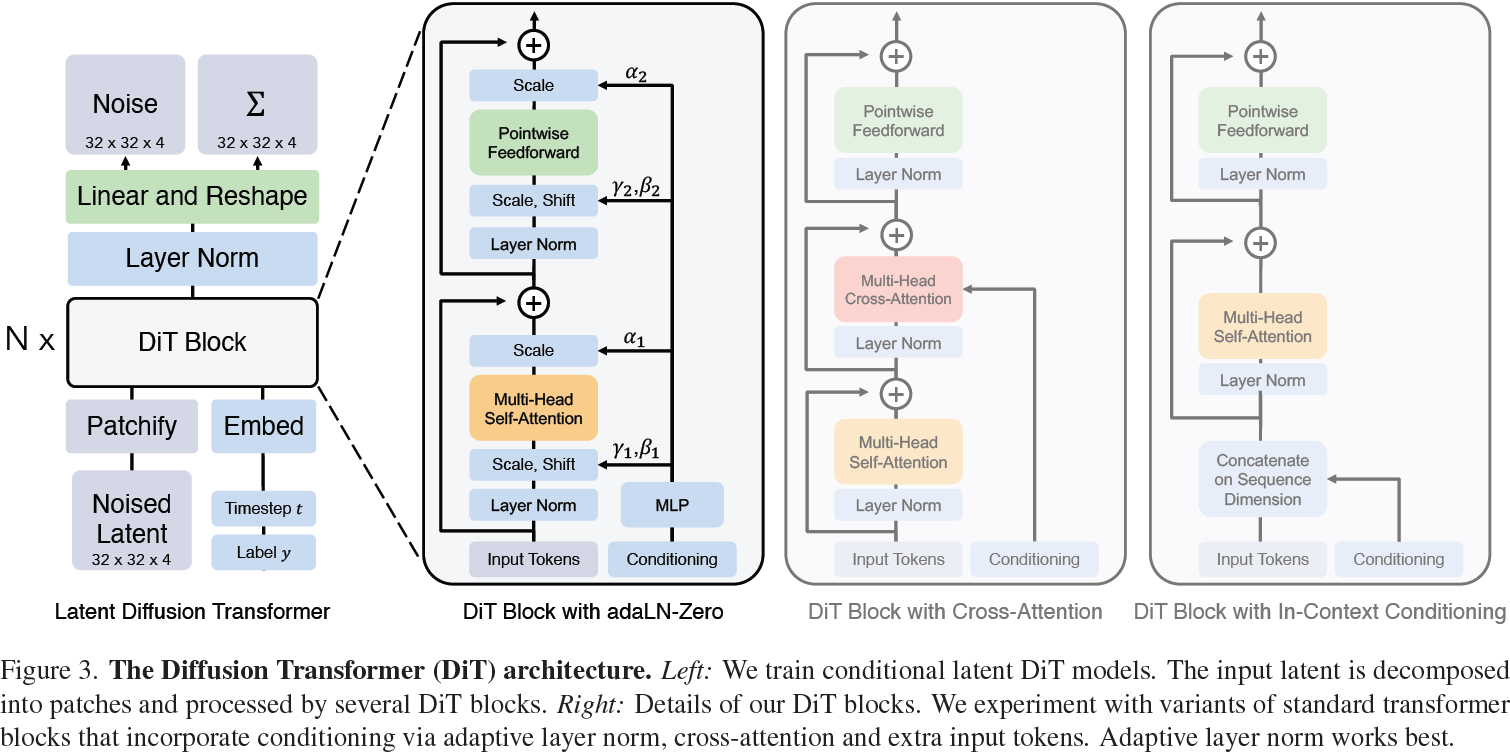
我们介绍了扩散 Transformer（Diffusion Transformers，简称DiTs），这是一种新的扩散模型架构。我们的目标是尽可能忠实于标准的 Transformer 架构，以保留其扩展性质。由于我们的重点是训练图像的 DDPM（Diffusion-Probabilistic Models，扩散概率模型），特别是图像的空间表示，DiT 基于 Vision Transformer（ViT）架构，该架构操作于图像的 patch 序列 [10]。DiT 保留了 ViTs 的许多最佳实践。图 3 显示了完整的 DiT 架构概述。在本节中，我们描述了 DiT 的前向传播，以及 DiT 类的设计空间组件。

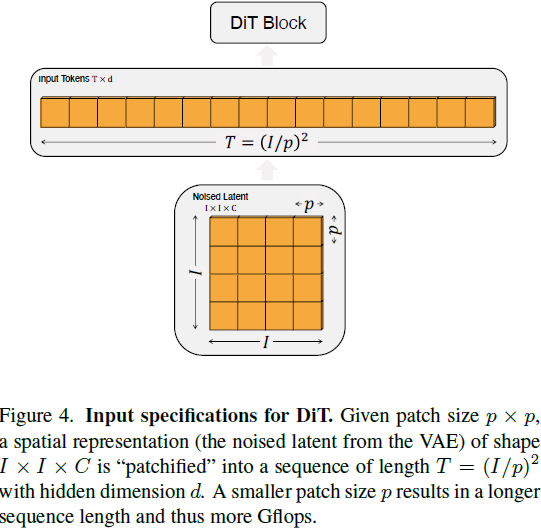
Patchify。DiT 的输入是一个空间表示 z（对于 256x256x3 的图像，z 的形状为 32x32x4）。DiT 的第一层是 “patchify”，它通过线性嵌入输入中的每个 patch，将空间输入转换为 T 个维度为 d 的标记序列。在 patchify 之后，我们对所有输入标记应用标准 ViT 的基于频率的位置嵌入（正弦-余弦版本）。由 patchify 创建的标记数 T 由 patch 大小超参数 p 确定。如图 4 所示，减半 p 将使 T 成倍增加，从而至少使 transformer 的总 Gflops 成倍增加。尽管这对 Gflops 有重要影响，但请注意，更改 p 对下游参数计数没有实质性影响。

（我们将 p = 2, 4, 8 添加到 DiT 的设计空间。）

DiT 设计。在 patchify 之后，输入标记由一系列 transformer 块处理。除了带噪声的图像输入外，扩散模型有时还处理额外的条件信息，如噪声时间步 t、类标签 c、自然语言等。我们探索了四个变体的 transformer 块，这些块以不同方式处理条件输入。这些设计在标准 ViT 块设计中引入了小但重要的修改。所有块的设计都显示在图 3 中。

• 上下文调节。我们简单地将 t 和 c 的向量嵌入作为输入序列中的两个额外标记附加在一起，对待它们与图像标记无异。这类似于 ViTs 中的 cls 标记，它允许我们在不进行修改的情况下使用标准的ViT 块。在最终块之后，我们从序列中删除调节标记。这种方法对模型引入了可忽略的新 Gflops。
• 交叉注意力块。我们将 t 和 c 的嵌入连接成一个长度为 2 的序列，与图像标记序列分开。Transformer 块被修改以在多头自注意块之后包括一个额外的多头交叉注意力层，类似于 Vaswani等人的原始设计 [60]，并且也类似于以类别标签为条件的?LDM 的设计。交叉注意力向模型添加最多的 Gflops，大约为 15% 的开销。
• 自适应层归一化（Adaptive layer norm，adaLN）块。在 GANs [2, 28] 和具有 UNet 骨干的扩散模型 [9] 中广泛使用自适应归一化层（adaptive normalization layer） [40] 后，我们尝试用自适应层归一化（adaLN）替换 Transformer 块中的标准层归一化层。与直接学习逐维缩放参数 γ 和移位参数 β 不同，我们从 t 和 c 的嵌入向量的总和中回归它们。在我们探索的三个块设计中，adaLN 添加的 Gflops 最少，因此是计算效率最高的。它还是唯一一种限制将相同函数应用于所有标记的条件机制。
• adaLN-Zero 块。在 ResNets 的先前工作中，发现将每个残差块初始化为同分布函数是有益的。例如，Goyal 等人发现在监督学习设置中，将每个块中的最终批归一化比例因子 γ 初始化为零可以加速大规模训练 [13]。扩散 U-Net 模型使用类似的初始化策略，在任何残差连接之前将每个块中的最终卷积层初始化为零。我们探索了adaLN DiT 块的修改，它执行相同的操作。除了回归 γ 和 β 之外，我们还回归了在 DiT 块内在任何残差连接之前立即应用的逐维缩放参数 α。对所有 α，我们初始化 MLP 输出零向量；这将完全初始化 DiT 块为同分布函数。与普通的 adaLN 块一样，adaLN-Zero 对模型添加的 Gflops 很小。

（我们在 DiT 设计空间中包括了上下文、交叉注意力、自适应层归一化和 adaLN-Zero 块。）

模型大小。我们应用 N 个 DiT 块的序列，每个块在隐藏维度大小为 d。遵循 ViT，我们使用共同缩放 N、d 和注意力头的标准 transformer配置 [10, 63]。具体而言，我们使用四个配置：DiT-S、DiT-B、DiT-L 和 DiT-XL。它们涵盖了各种模型大小和 Gflops 分配，从 0.3 到 118.6 Gflops，使我们能够评估缩放性能。表 1 提供了配置的详细信息。

（我们在 DiT 设计空间中添加了 B、S、L 和 XL 配置。）

Transformer 解码器。在最后的 DiT 块之后，我们需要将图像标记的序列解码为输出噪声预测和输出对角协方差预测。这两个输出的形状与原始的空间输入相等。我们使用标准的线性解码器来完成这个任务；我们将最终的层归一化（如果使用 adaLN，则是自适应的）应用于每个标记，并将每个标记线性解码为一个 p x p x 2C 的张量，其中 C 是输入到 DiT 的空间输入中的通道数。最后，我们重新排列解码的标记以获得预测的噪声和协方差。

（我们探索的完整 DiT 设计空间包括补丁大小、transformer 块架构和模型大小。）

4. 实验