【算法】使用BFS算法（队列、哈希等）解决最短路径问题（C++）

1. 前言

1.1 什么是最短路问题？

我们这里主要探讨权值为1的最短路问题。

1.1.1 什么是权值？

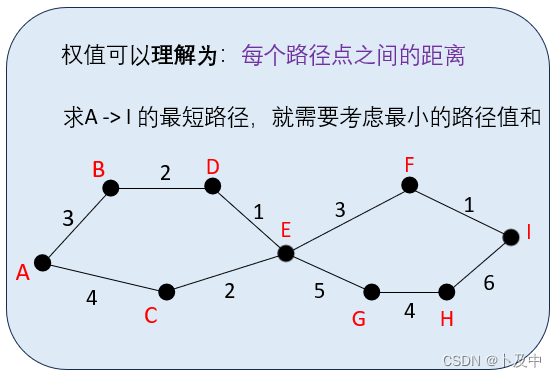
而对于权值为1的最短路问题：即不考虑每个路径点的值，只考虑最短的路径是什么即可。

1.2 如何解决此类最短路径？

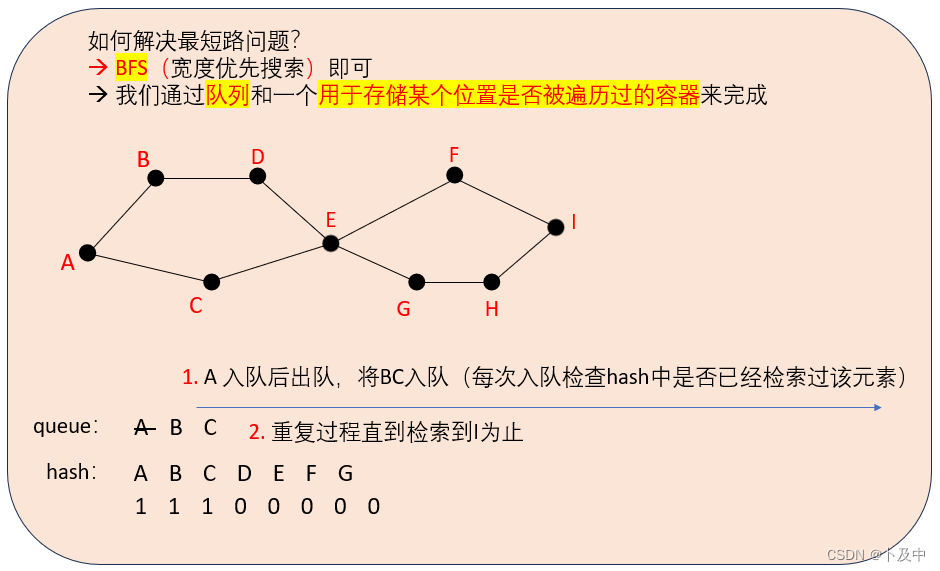
1.3 BFS解最短路径 前提 （FloodFill / 洪流问题）

关于如何用dfs或bfs算法对二维数组进行搜索，可以看下面的一篇文章：

【算法】bfs与dfs算法解决FloodFill（洪流）问题（C++）

---

2. 算法题

1926.迷宫中离入口最近的出口

思路

• 题目分析：本题是一道经典的迷宫问题，我们可以将其转化理解为上图所示。
• 主思路：BFS，我们从起始位置开始，一层一层像外扩（上下左右四个方向都执行扩展）直到扩展到边界（即出口），此时扩展的层数就是最短的路径
• 思路步骤：
  1. 创建一个visited数组，用于标记迷宫每位是否走过。
  2. 创建队列，存储迷宫中每一位的下标（pair类型）
  3. 将起始位置下标加入到队列中，进行循环，直至队列为空
     • 循环中每次++step，并执行sz次（队列元素个数）扩充，每次扩充即向上下左右四个方向扩。
     • 每向一个方向扩后，检查该位置是否为终点。
  4. 根据前言中的洪流问题，结合下面的代码理解！

代码

class Solution {
public:
    int dx[4] = {0, 0, -1, 1}; // 标记x, y 坐标的四个方向走向
    int dy[4] = {-1, 1, 0, 0};

    int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
        int step = 0; // 记录走过的步数
        int a = entrance[0], b = entrance[1]; // 提取起始位置坐标
        int m = maze.size(), n = maze[0].size();
    
        vector<vector<bool>> visit; // 标记是否被遍历过
        visit.resize(m, vector<bool>(n, false)); // 初始化
        visit[a][b] = true;
        queue<pair<int, int>> q; // 存储位置坐标
        q.push({a, b});

        while(!q.empty())
        {
            ++step;
            int sz = q.size(); // 按层遍历当前队中元素
            for(int j = 0; j < sz; ++j)
            {
                auto [_x, _y] = q.front(); // 提取队头元素坐标
                q.pop();
                for(int i = 0; i < 4; ++i) // 搜索上下左右四个位置
                {
                    int x = _x + dx[i];
                    int y = _y + dy[i];
                    if((x < m && x >= 0) && (y < n && y >= 0) && !visit[x][y] && maze[x][y] == '.')
                    {
                        // 判断此时是否是终点
                        if(x == 0 || x == m - 1 || y == 0 || y == n - 1) return step;
                        q.push({x, y});
                        visit[x][y] = true;
                    }
                }
            }
        }
        return -1;
    }
};

---

433.最小基因变化

思路

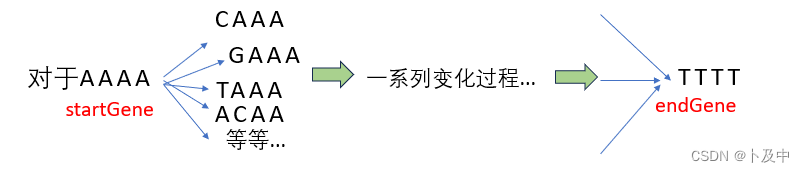
• 题意分析：通过将字符串startGene 转化为 endGene，且每次变化都在数组bank中存在，求转化的最少次数。

• 当我们把startGene 转化 求得最终结果endGene时，如下图所示，其本质上属于 边权为1的最路径问题，据此我们有以下思路：
  

• 解法：哈希表 + 队列 BFS

代码

• 对于下面的代码，主要就一处进行解释：

• 为什么要用临时字符串tmp?

  • 对于两层for循环：每次外层循环只对一个字符进行更改，使用临时字符串tmp，而不对字符串t一直进行更改
  • （比如第一次外层循环AAAA->…->TAAA后，由于更改的是字符串tmp，此时t依然是AAAA，第二次外层循环执行时依然是从AAAA->ACAA开始）

int minMutation(string startGene, string endGene, vector<string>& bank) {
    unordered_set<string> visited; // 用于记录所有检索过的状态
    unordered_set<string> hash(bank.begin(), bank.end()); // 记录基因库中的所有序列
    string change = "ACGT"; // 用于对序列中字符进行更改

    // 处理边界情况
    if(startGene == endGene) return 0;
    if(!hash.count(endGene)) return -1;

    queue<string> q; // 创建队列存储满足条件的序列变化
    q.push(startGene);
    visited.insert(startGene);

    int minCount = 0; // 最小变化次数（最终结果）
    while(q.size())
    {
        ++minCount;
        int sz = q.size();
        while(sz--) // 队列大小即为 下一次待变化的序列数
        {
            string t = q.front(); // 提取当前序列
            q.pop();
            for(int i = 0; i < 8; ++i) // 每个序列有8个字符，对所有字符进行转化
            {
                string tmp = t; // 每次循环只对一个字符进行更改，使用临时字符串tmp，使不对t一直进行更改（比如GAAA->TAAA后，继续进）
                for(int j = 0; j < 4; ++j) // 每个字符进行"ACGT"四种变化
                {
                    tmp[i] = change[j]; // 更改字符
                    if(hash.count(tmp) && !visited.count(tmp)) // 此时序列是合法的更改（在bank中）
                    {
                        if(tmp == endGene) return minCount; // 此时的合法序列为最终结果，返回
                        q.push(tmp);
                        visited.insert(tmp);
                    }
                }
            }
        }
    }
    return -1;
}

---

127.单词接龙

思路

• 题意分析：这道题与上一道基因变化很类似，代码编写也十分类似，，下面是思路：
• 解法：哈希表 + 队列BFS
  1. 题目要求找到 最短转换序列的 最小单词数，而beginWord自身也算一个，则在创建结果变量时我们初始化为1。
  2. 哈希表：
     • visited 用于记录所有检索过的单词，使不重复改变
     • hash 标记字典wordList的所有单词
  3. 对于两个for循环：
     • 外层循环：通过提取队头字符串，对该单词进行遍历，执行对每一位的更改
     • 内层循环：对每一位更改的具体操作，从’a’~‘z’，依次对字符进行替换

代码

int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
    unordered_set<string> hash(wordList.begin(), wordList.end());
    unordered_set<string> visited;

    if(!hash.count(endWord)) return 0;

    queue<string> q;
    q.push(beginWord);
    visited.insert(beginWord);
    
    int minCount = 1; // 首先加上beginWord自身
    while(q.size())
    {
        ++minCount;
        int sz = q.size();
        while(sz--)
        {
            string t = q.front();
            q.pop();
            for(int i = 0; i < t.size(); ++i) // 对每个单词的每一位进行改变
            {
                string tmp = t;
                for(char ch = 'a'; ch <= 'z'; ++ch)
                {
                    tmp[i] = ch;
                    if(!visited.count(tmp) && hash.count(tmp))
                    {
                        if(tmp == endWord) return minCount;
                        q.push(tmp);
                        visited.insert(tmp);
                    }
                }
            }
        }
    }
    return 0;
}

---

675.为高尔夫比赛砍树

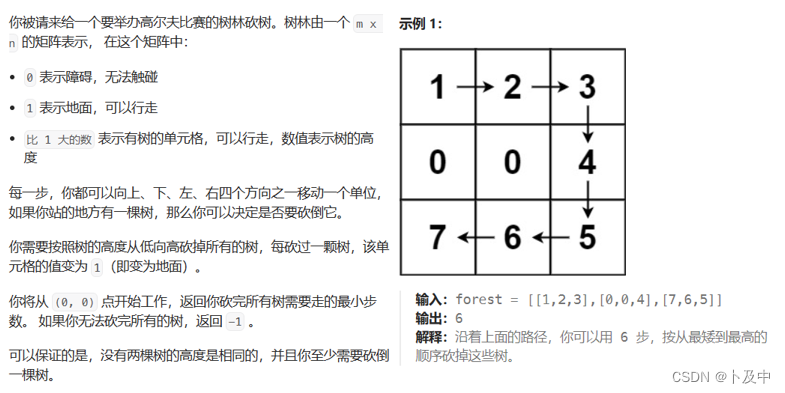
思路

• 题意分析：题目要求按照从低到高的顺序砍树，求砍树所走的最小步数。这道题实则是一个对洪流和迷宫问题的结合考研，编写代码时也是如此。
• 对于示例一：
  
• 解法：队列BFS
• 主要思路：
  1. 利用二维数组存储树的下标，并排序得到砍树的顺序
     • 直接两层循环创建数组，并自定义比较函数排序
  2. 执行砍树过程
     • 从起始位置开始，每一小部分（1->2）都进行依次bfs，bfs用于寻找从起始树到目标树的步数。
     • 如果其中一个部分无法执行，最终就无法执行
  3. bfs
     • 创建visited与dx、dy全局数组
     • 在进行多次 BFS 搜索时，每次搜索的起点和终点都可能不同，因此需要将访问标记数组 visited 重置，以免对下一次搜索结果产生影响。
     • 随后利用队列进行bfs的具体步骤，我们在floodfill写过很多，这里不再赘述，看代码就能理解。

代码

class Solution {
public:
    int m, n; // 定义全局变量便于访问
    int cutOffTree(vector<vector<int>>& forest) {
        m = forest.size(), n = forest[0].size();
        // 1. 通过容器存储 需要砍的树
        vector<pair<int, int>> trees;
        for(int i = 0; i < m; ++i)
            for(int j = 0; j < n; ++j)
                if(forest[i][j] > 1) trees.push_back({i, j}); // 大于1的是待砍的树

        // 1.5 排序，找出 砍树顺序
        sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2){
            return forest[p1.first][p1.second] < forest[p2.first][p2.second];
        });

        // 2. 砍树步骤
        int bx = 0, by = 0; // 起始位置 坐标
        int minCount = 0;
        for(auto &[a, b] : trees)
        {
            // step : 从当前位置到下一位置的步数
            int step = bfs(forest, bx, by, a, b); // 后四个参数分别为起始位置的x, y坐标以及目标位置的x, y坐标
            if(step == -1) return -1; // 其中一棵树无法砍到，最终就无法砍掉所有的树
            minCount += step;
            bx = a, by = b; // 更新下一次的起始位置
        }
        return minCount;
    }

    bool visited[51][51]; // 用于记录当前位置是否被检索过
    int dx[4] = {0, 0, -1, 1};  // 用于x坐标的上下左右方向更新
    int dy[4] = {-1, 1, 0, 0};  // 用于y坐标的上下左右方向更新
    int bfs(vector<vector<int>> &forest, int beginX, int beginY, int endX, int endY)
    {
        if(beginX == endX && beginY == endY) return 0;

        memset(visited, false, sizeof(visited));
        queue<pair<int, int>> q; // 创建队列用于搜索
        q.push({beginX, beginY});
        visited[beginX][beginY] = true;

        int step = 0;
        while(q.size())
        {
            ++step;
            int sz = q.size();
            while(sz--)
            {
                auto [a, b] = q.front(); // 提取队头元素，进行上下左右四个方向的搜索
                q.pop();
                for(int i = 0; i < 4; ++i)
                {
                    int x = a + dx[i], y = b + dy[i];
                    if((x >= 0 && x < m) && (y >= 0 && y < n) && !visited[x][y] && forest[x][y]) // 在合法范围内对所有未被检索的位置执行：
                    {
                        if(x == endX && y == endY) return step;
                        q.push({x, y});
                        visited[x][y] = true;
                    }
                }
            }
        }
        return -1;
    }
};