【知识积累】深度度量学习综述

原文指路：https://hav4ik.github.io/articles/deep-metric-learning-survey

Problem Setting of Supervised Metric Learning

深度度量学习是一组旨在衡量数据样本之间相似性的技术。

Contrastive Approaches

对比方法的主要思想是设计一个损失函数，直接将具有相同标签的样本（即“相似”样本）的嵌入放在一起，并让不相似样本的嵌入彼此远离，因此得名“对比” 。这些方法有时在被称为“直接”方法，因为它们直接应用了度量学习的定义。

Contrastive Loss

这是度量学习的经典损失函数。 对比损失（Chopra et al. 2005）是最简单的损失之一和最直观的训练目标。

Triplet Loss

Triplet Loss 三元组损失（Schroff et al. 2015） 是迄今为止最流行、最广泛使用的度量学习损失函数。使Triplet Loss在实践中充分发挥作用的关键因素是负样本挖掘。


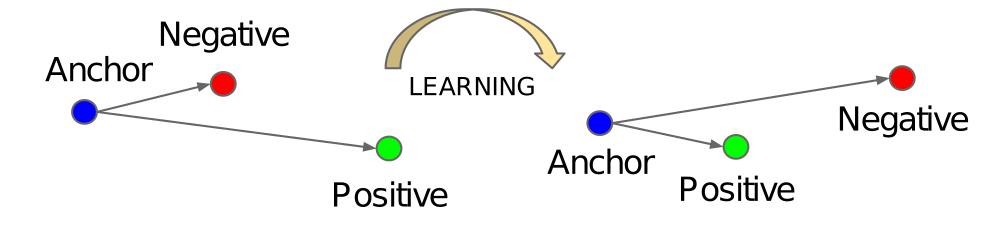
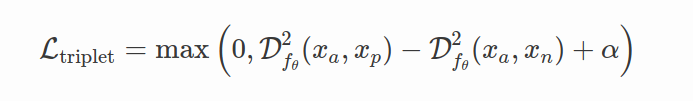
$x_a$ ：anchor样本，$x_p$：positive样本， $x_n$：negative样本。
$\alpha$是为了不让所有样本分布到同一点。

Improving the Triplet Loss

Quadruplet Loss 四元组损失(Chen et al. 2017) is an attempt to make inter-class variation of the features $f_{\theta }(x)$ larger and intra-class variation smaller, contrary to the Triplet Loss that doesn’t care about class variation of the features.

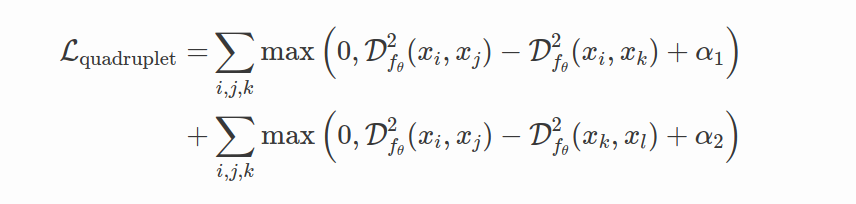
最小类间距离要求要大于最大类内距离。
另一篇相似的论文中定义为：

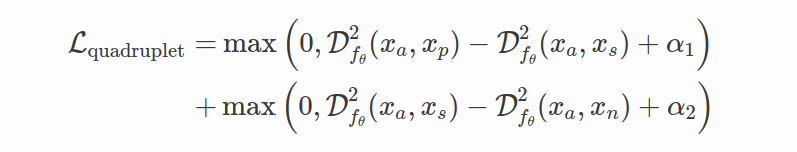
Structured Loss (Song et al. 2016) 被提出是为了提高 Triplet loss 的采样有效性并充分利用每批训练数据中的样本。

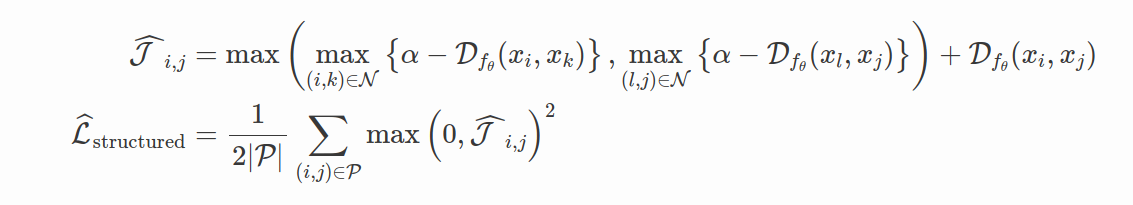
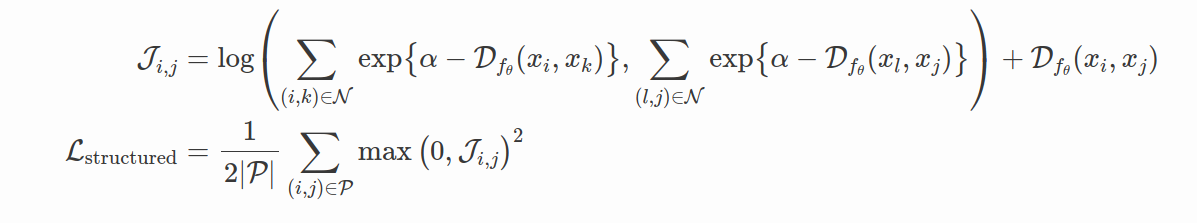
N-Pair Loss （Sohn，2016） 论文详细讨论了其中一项Triplet Loss 的主要局限性，同时提出了与使用正负对的 Structured Loss 类似的想法：

Moving Away from Contrastive Approaches

在监督深度度量学习背景下，无数研究论文试图解决三元组损失的问题和局限性，结果很明显：学习直接最小化/最大化相同类别/不同类别的样本之间的欧氏距离或许不是正确的方法，这种方法有两个主要问题：

1. 拓展问题。很难确保具有相似标签的样本江北拉到一起到空间中的公共区域。Quadruplet Loss 只能提升多变性，Structured Loss只能强制执行批次中样本的本地结构，而不是全局结构。尝试以全局目标直接解决此问题（Magnet Loss，Rippel et al. 2015 和 Clustering Loss， Song 等人，2017）由于可扩展性问题而未能获得太多关注。
2. 采样问题：所有尝试直接最小化/最大化样本之间距离的深度度量学习方法在很大成都上依赖于复杂的样本挖掘技术，该技术为每个训练批次选择最有用的样本进行学习。这在本地设置中非常不方便（考虑GPU利用率），并且在分布式训练设置中可能会变得相当成问题。

Center Loss

中心损失是解决上述两个问题的首批成功尝试之一。
首先考虑Softmax损失。softmax目标的判别力不够，即使在MNIST这样简单的数据及上仍然存在显著的类内变化。

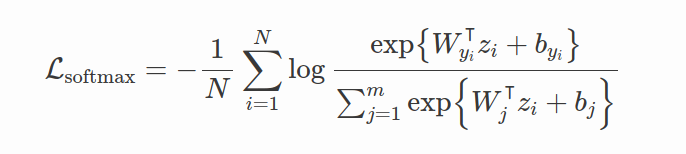
所以center loss的想法是在softmax loss中添加一个新的正则化项，将特征拉到相应的类中心：

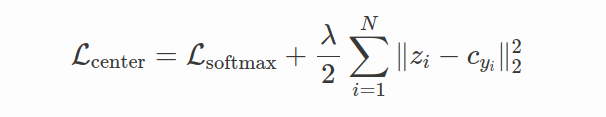
中心损失通过提供类中心来解决拓展问题，从而强制样本聚集到相应的类中心，由于我们不再需要进行困难的样本挖掘，故解决了样本问题。虽然中心损失也有自己的问题和限制，但仍是一项开创性的工作，有助于将深度度量学习的方向引导到当前的形式。

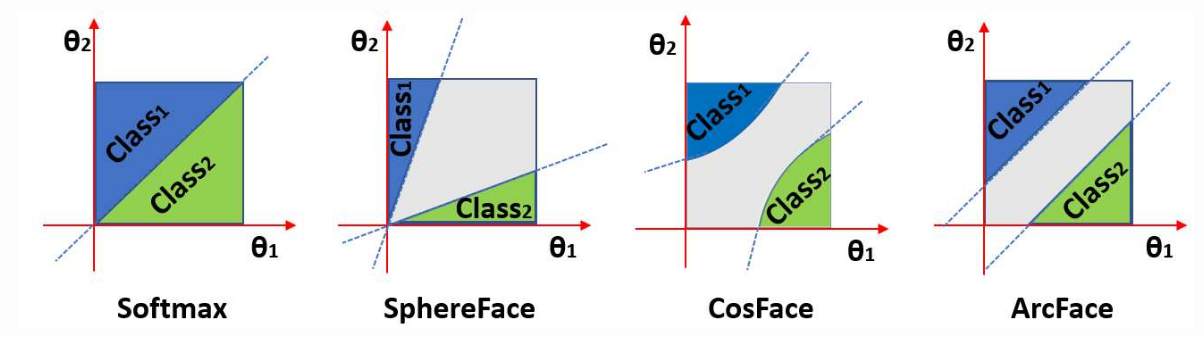
SphereFace

center loss的一个明显问题是中心点的选择。首选，不能保证具有较大的类间变化。因为接近于0的簇从正则化项中的受益更少。为了公平对待每一类，为什么不强制类中心和中心的距离相同呢？让我们将其映射到超球面！这就是SphereFace背后的主要思想。从softmax loss进行以下修改：

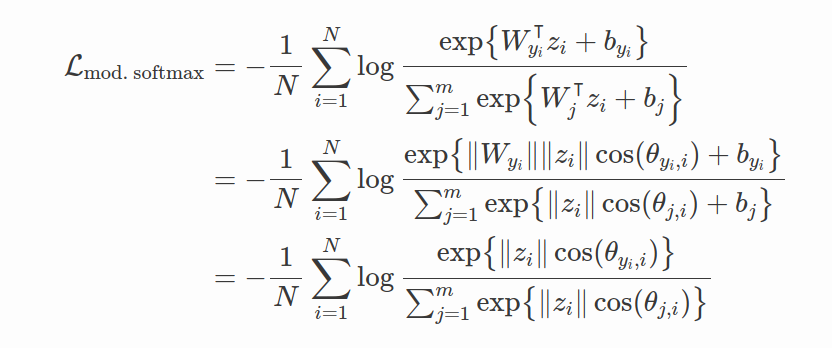
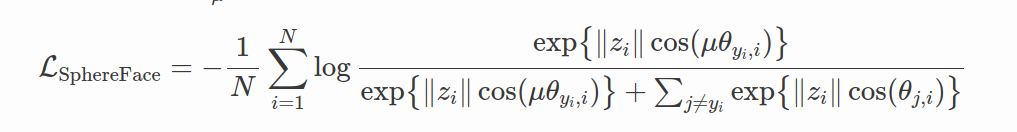
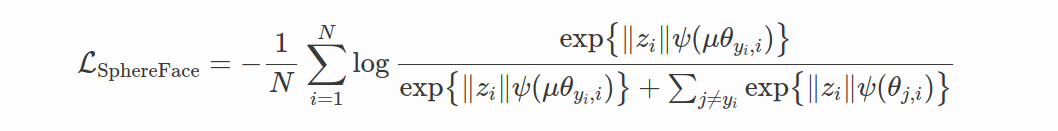
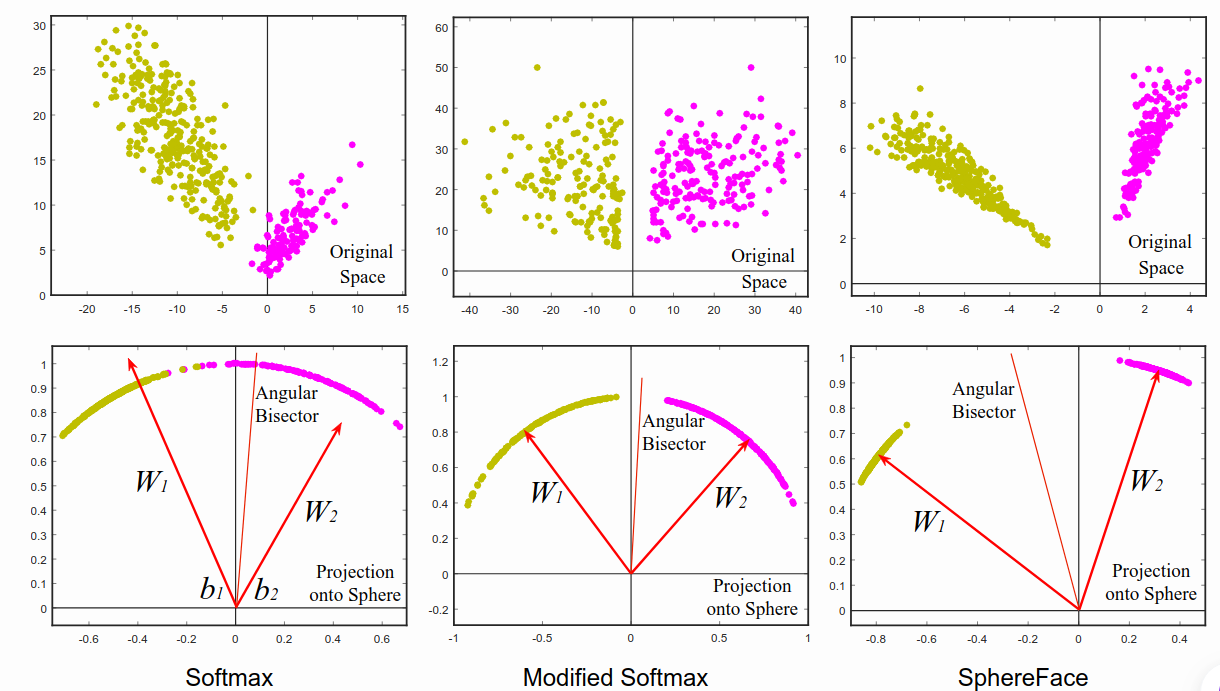
Difference between Softmax, Modified Softmax, and SphereFace. A 2D features model was trained on CASIA data to produce this visualization. One can see that features learned by the original softmax loss can not be classified simply via angles, while modified softmax loss can. The SphereFace loss further increases the angular margin of learned features.

State-of-the-Art Approaches

SphereFace 的成功催生了大量基于角距离和角度间隔思想的新方法。
请注意，这些方法仅适用于监督深度度量学习设置。 在无监督环境中，或者当我们在测试期间有大量非分布样本时，对比学习方法仍然是最不错的选择之一。

CosFace

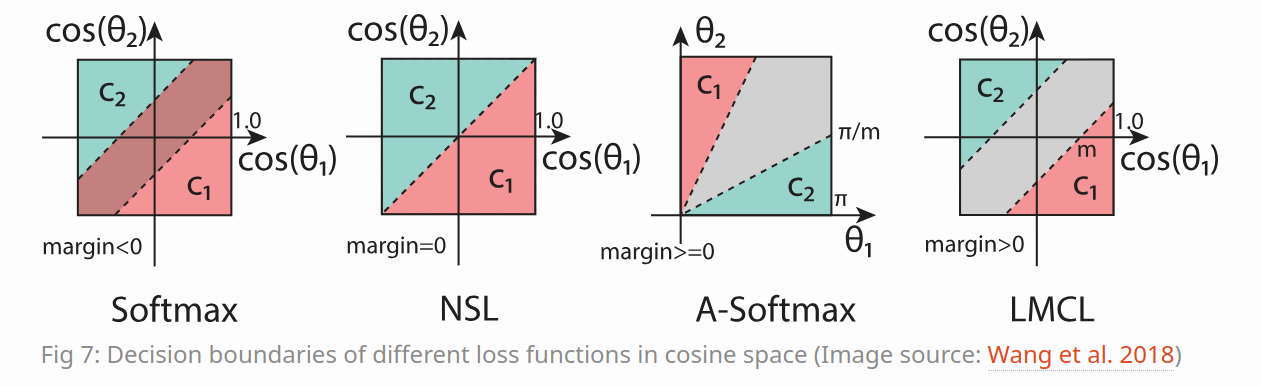
SphereFace的决策边界在角度空间上定义为cos(μθ1)=cos(θ2)，由于余弦函数的非单调性，优化困难。 为了克服这一困难，我们必须采用一种额外的技巧，为 SphereFace 提供一个专门的分段函数。 更重要的是，SphereFace 的决策裕度取决于 θ，这导致不同类别的裕度不同。 结果，在决策空间中，一些类间特征具有较大的余量，而另一些则具有较小的余量，这降低了判别能力。

CosFace（Wang et al. 2018）提出了一种更简单但更有效的方法来定义边距。 该设置与 SphereFace 类似，对权重矩阵 W 的行进行归一化，即 $\Vert Wj\Vert =1$，并将偏差归零 b=0。 此外，还对特征 z（由神经网络提取）进行归一化，因此 $\Vert z\Vert =1$。 CosFace 目标定义为：

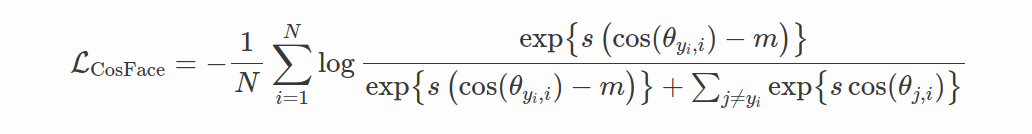
其中 s 称为缩放参数，m 称为边距参数。 与SphereFace中一样，θj,i表示第i个特征向量zi和Wj之间的角度，并且$W_j^T{z}_i=cos{\theta }_{j,i}$，因为$\Vert Wj\Vert =\Vert zi\Vert =1$。 从视觉上看，它看起来如下：

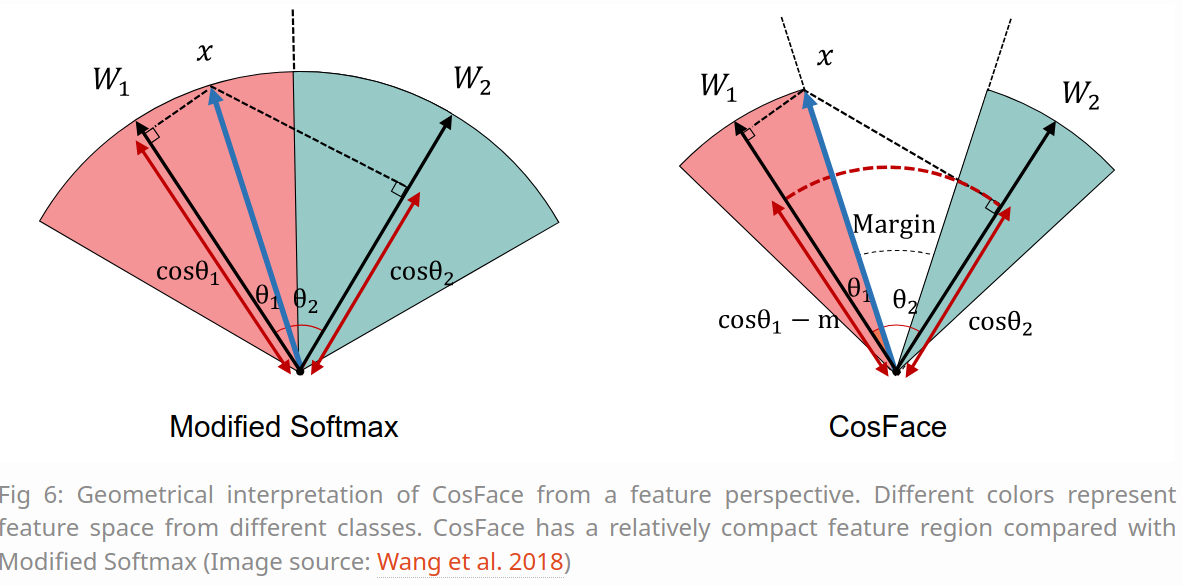
从特征角度对CosFace进行几何解释。 不同的颜色代表不同类别的特征空间。 与 Modified Softmax 相比，CosFace 具有相对紧凑的特征区域。
选择正确的尺度值s和裕度值m非常重要。 在 CosFace 论文中，表明 s 应该有一个下界，以至少获得预期的分类性能。 令 C 为类别数。 假设学习到的特征向量分别位于超球面的表面上并以相应的权重向量为中心。 令 $P_W$ 表示类中心的期望最小后验概率（即 W）。 s 的下界由下式给出：

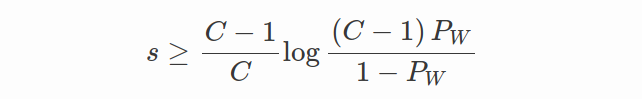
假设所有特征都很好地分离，则 m 的理论变量范围应该是：

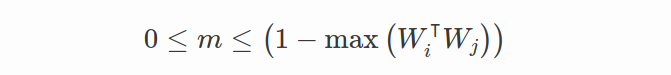
假设Modified Softmax损失的最优解应将权重向量均匀分布在单位超球面上，则margin m的可变范围可以推断如下:

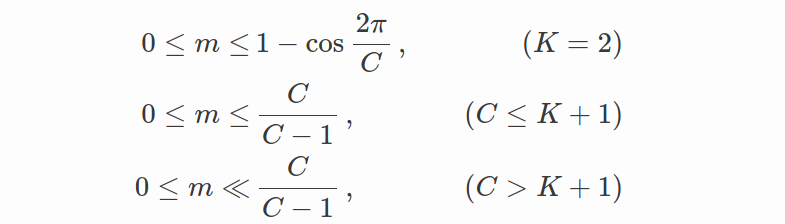
其中 K 是学习特征的维度。 不等式表明，随着类数量的增加，类间余弦间隔的上限相应减小。 特别是，如果类的数量远大于特征维度，则余弦间隔的上限将变得更小。

ArcFace

ArcFace（Deng 等人，2019）与 CosFace 非常相似，并且解决了 CosFace 描述中提到的 SphereFace 的相同限制。 但是，它不是在余弦空间中定义边距，而是直接在角度空间中定义边距。设置与CosFace相同，要求最后一层权重和特征向量应归一化，即∥Wj∥=1和∥z∥=1，最后一层偏差应等于0（b=0）。 ArcFace 目标定义为：

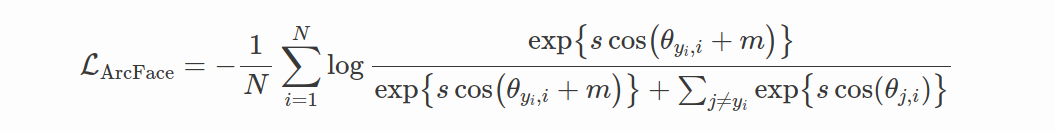
人脸识别数据集被用作 CosFace、ArcFace 和其他角度间隔方法的标准基准，因为它是深度度量学习最流行的应用。 以下是一些损失函数的消融研究和比较：

AdaCos — how to choose s and m?

对于 CosFace 和 ArcFace 来说，缩放参数 s 和边距 m 的选择至关重要。 这两篇论文都很少分析这些参数的影响。 为了回答如何选择 s 和 m 的最佳值的问题，Zhang 等人。 (2019) 对基于余弦损失的超参数进行了出色的分析。

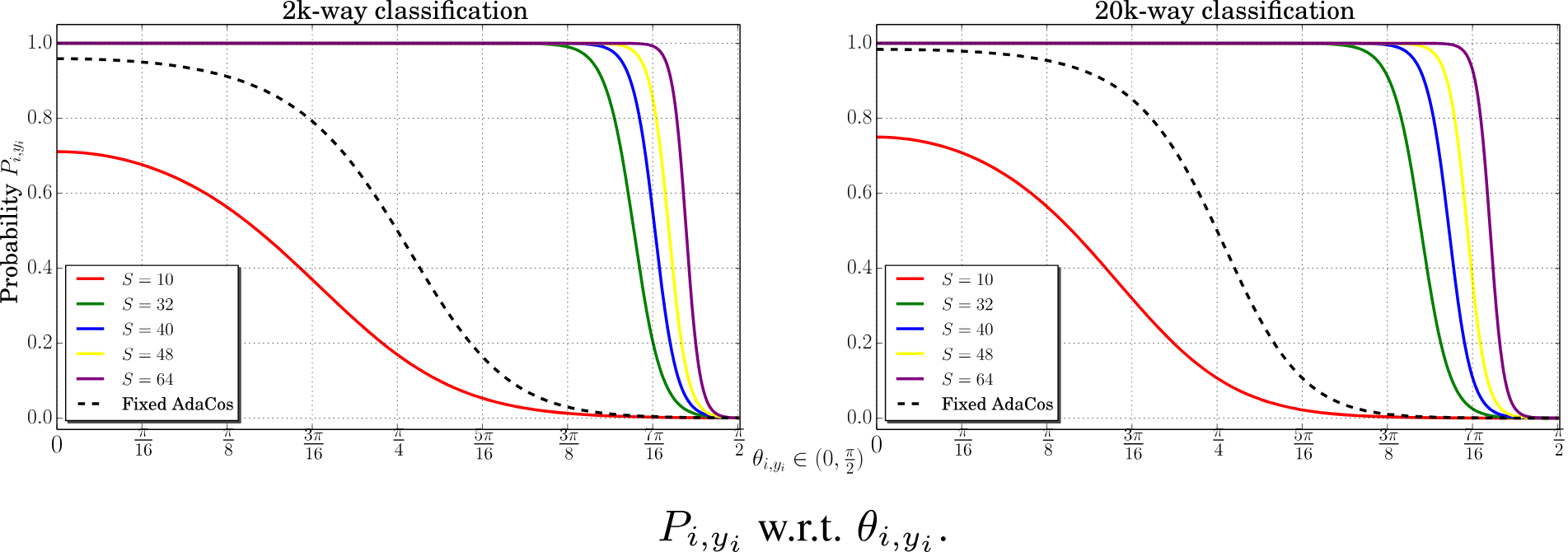
正如我们所看到的，当缩放参数 s 的值很小时（例如 s=10），Pi,j 的最大值无法达到 1。这是不可取的，因为即使网络对样本非常有信心， 损失函数仍然会惩罚正确的结果。 另一方面，当 s 太大时（例如 s=64），即使 θi,yi 很大，也会产生非常高的概率，这意味着损失函数无法惩罚错误。

增加 margin 参数会使 $P_{i,y_i}$ 的概率曲线向左移动。 较大的margin 会导致较低的概率 $P_{i,y_i}$，因此即使角度 ${\theta }_{i,y_i}$ 较小，损失也会较大。 这也解释了为什么基于margin的损失对相同的 ${\theta }_{i,y_i}$ 比没有margin的基于余弦的损失提供更强的监督。

虚线“固定 AdaCos”曲线。 在 AdaCos 论文中，提出了以下固定的缩放参数 s 值：

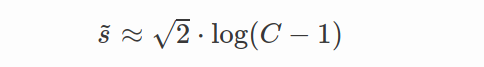
C 是类别数量。

Sub-Center ArcFace

每个类别只有一个中心（如 ArcFace、CosFace 等）会导致以下问题：

如果类内样本方差很高，那么强制压缩到嵌入空间中的单个簇是没有意义的。
对于大型且嘈杂的数据集，嘈杂/不良样本可能会错误地生成较大的损失值，从而损害模型训练。

Sub-Center ArcFace（Deng et al. 2020）通过引入子中心解决了这个问题。 这个想法是每个类别都有多个类中心。 大多数样本将收缩到主导中心，而嘈杂或困难的样本将被拉到其他中心。 Sub-Center ArcFace 的公式看起来与 ArcFace 几乎相同，除了角度之外，定义为与 K 个子中心 Wj,1…Wj,K 中最近的子中心的角度（而不是像 ArcFace 中那样仅与类中心的角度）。：

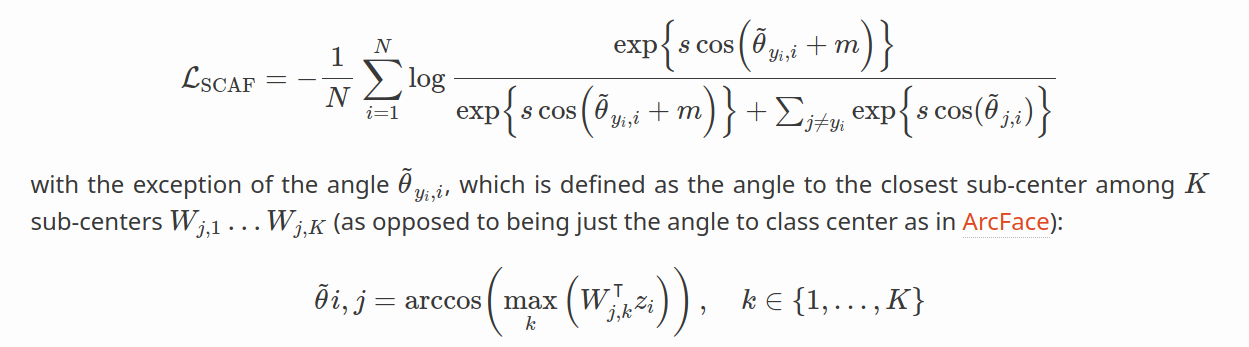
ArcFace with Dynamic Margin

ArcFace with Dynamic Margin（Ha et al. 2020）是 2020 年 Google Landmarks Challenge 第三名获奖者提出的 ArcFace 的简单修改。为不同类别设置不同边距值的主要动机是数据集的极端不平衡 - 某些类别 可以有数万个样本，而其他类可能只有10个样本。

为了使模型在严重不平衡的情况下更好地收敛，较小的类别需要有更大的余量，因为它们更难学习。 第 i 类的margin值 mi 的建议公式很简单：

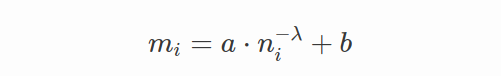
其中ni是第i类训练数据中的样本数量，a、b是控制边际上限和下限的参数，λ>0决定边际函数的形状。 与 Sub-Center ArcFace 一起使用，该方法比 ArcFace 更有效。

---

Getting Practical: a Case Study of Real-World Problems

遗憾的是，众所周知的事实是，在酷炫新方法的学术基准上报告的 SOTA 结果可能无法反映其在现实世界问题中的表现。 这就是为什么在本节中，我们将了解如何在现实世界的问题中使用深度度量学习，以及使用哪些方法来获得最佳结果。

Kaggle: Humpback Whale Challenge (2019)

Kaggle 座头鲸挑战赛的主要目标是确定给定的鲸鱼照片是否属于 5004 条已知鲸鱼中的其中之一，或者是否是一头以前从未观察到的新鲸鱼。这场比赛的令人费解的地方是巨大的类别失衡。 对于 2000 多个类，只有一个训练样本。 更重要的是，比赛的重要部分是对给定的鲸鱼是否是新的进行分类。

虽然本次比赛中表现最好的选手使用了很多方法技巧，但我将只关注深度度量学习方法。 对顶级团队（即金牌得主）使用的方法的简短调查：

ArcFace 由第二名、第三名、第六名和第九名奖牌获得者使用。
CosFace 也被用作第九名解决方案的一部分。
Triplet Loss 由第二名（与 ArcFace 和 Focal 损失结合）和第九名解决方案（与局部关键点匹配结合）使用。 第二名还使用焦点损失来对抗类别不平衡。
第四名使用了一个很好的旧暹罗网络，给定两张图像，该网络将判断它们是否来自同一头鲸鱼。 他们还使用 SIFT 和 ROOTSIFT 进行关键点匹配。
有趣的是，第一名的团队仅使用分类模型并结合一些grandmaster’s wizardry 就取得了领先。
在本次比赛时，ArcFace 和 CosFace 还是相当新且未经测试的技术，因此并未被顶级团队广泛采用。 我们将在接下来的案例研究中看到，ArcFace 和 CosFace 将成为顶尖执行者最常用的方法。

Kaggle: Google Landmarks Challenge (2020)

Google 地标挑战赛是一项大规模竞赛，涉及超过 20 万个人造或自然地标的超过 5,000,000 张图像。 比赛分为2个赛道：

检索赛道——将输入图像中的特定对象与参考图像目录中该对象的所有其他实例进行匹配。 可以将其视为 Google 的反向图像搜索功能。
识别赛道——识别对象的特定实例，例如尼亚加拉大瀑布与任何瀑布的区别。

除了该数据集的巨大规模之外，还有许多挑战使其成为深度度量学习技术的理想测试平台：

类别失衡。 对于埃菲尔铁塔等热门地标，可能有数千张图像，而西雅图的一个不太知名的船库每类的图像少于 10 张。
现实世界的条件。 为了模拟真实环境，只有 1% 的测试图像位于地标的目标域内，而 99% 是域外图像。
嘈杂的数据。 数据是在众包环境中收集的，因此训练集中预计会出现不正确的标签和低质量的域外样本。
类内变异性。 由于同一类别的图像可以包括室内和室外视图，以及与类别间接相关的图像，例如博物馆中的绘画。
很难评估这一挑战的重要性。 本次比赛中开发的方法将用于以下所有度量学习比赛。 提供图像搜索服务的大公司也密切关注着这场竞争。

像往常一样，获胜的解决方案包含很多技巧和魔法。 然而，在这篇博文中，我只会对表现最好的团队使用的度量学习方法进行简短回顾：

前 100 名中的所有参赛者都使用了 ArcFace、CosFace 或这些方法的某些变体。这与之前的 Google Landmarks 竞赛形成了巨大对比，其中 Triplet Loss 及其变体是最受欢迎的。第一名获奖者（识别赛道） 与所有其他团队相比，能够解决域外测试图像问题。 他们设计了一个推理过程，考虑了测试图像、地标图像和非地标图像之间的全对相似性。 第三名获奖者使用了带有动态边距的 Sub-Center ArcFace。 令人惊讶的是，他们仅通过原始度量学习就能取得这样的结果（与第四名团队相比有巨大差距），而不像其他表现最好的团队那样依赖复杂的后处理或局部特征匹配。
第一名（识别）和第三名（识别）团队开发的方法的组合可以组合成强大的图像识别和检索算法。
前 100 名中的所有参赛者都使用 GeM（p=3）和 GAP 池化方法，然后是线性层。这些池化方法之间没有明显的区别。 一些团队也尝试在 GeM 中训练 p，但性能提升甚微。
一般网络架构看起来与以下模式非常相似：

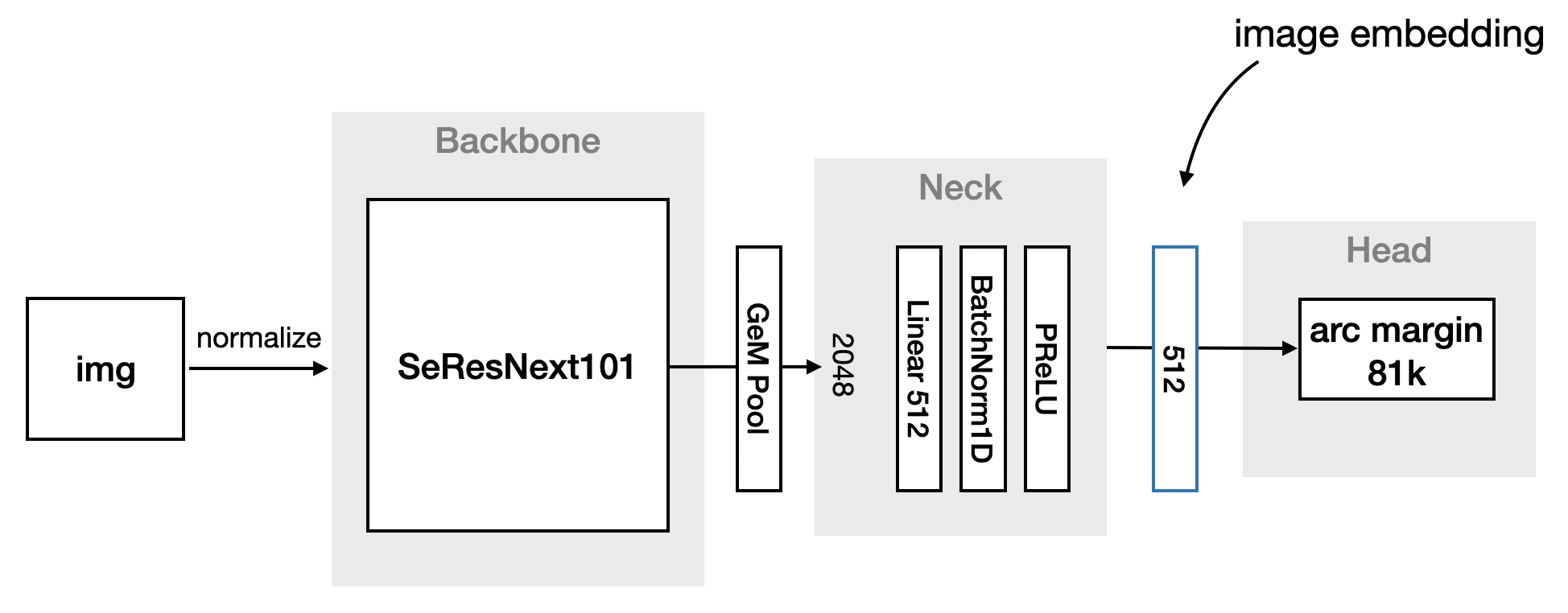
在 ArcFace 之上使用加权交叉熵，第一名解决了类别不平衡问题。 第五名提出了另一种方法，在 ArcFace 之上使用focal loss和标签平滑。
如果没有复杂的后处理，仅靠普通 ArcFace 似乎不足以在排行榜上获得较高的排名。 识别赛道上的顶级团队（即第二名和第七名）还依赖于 SuperPoint + SuperGlue 的局部特征匹配，这是特征匹配中最先进的组合。
有趣的是，但每个人都尝试了 Dynamic AdaCos（Zhang 等人，2019），因为发表的论文中的结果非常有希望。 但没有人成功做到这一点。
在我看来，在这次比赛之后，上述方法列表成为了 Kaggle 平台上 Metric Learning 比赛的标准。

Kaggle: Shopee Price Match Guarantee (2021)

与上述两场比赛相比，本次比赛有很大不同。 它涉及文本数据的度量学习。 给定某个产品的图像及其描述，任务是通过图像和文本描述在测试集中找到相似的产品（在训练期间未见过）。

这次比赛非常具有挑战性，因为训练集非常小（34k 图像），但测试集非常大，并且比训练集（70k 图像）更加多样化。 而且，测试集中的很多产品类别并未在训练集中呈现。

这两个挑战意味着顶级竞争对手被迫设计非常复杂的后处理管道、查询扩展，并严重依赖本地特征和文本信息。 不过，看看深度度量学习在本次比赛中的应用仍然很有用：

ArcFace 和 CosFace 被许多顶级团队使用，包括第一名、第四名和第八名获胜解决方案。 有趣的是，它被用来学习图像和文本嵌入！ 这太酷了——不仅限于图像数据！
第二名团队使用了 ArcFace 的变体，称为 Curriculum Face（Huang 等人，2020）。 据他们称，这个损失函数比 ArcFace 及其变体要好得多。
见证第三名队伍使用 Triplet Loss 的回归是非常有趣的。 他们也尝试了 ArcFace，但奇怪的是，他们的团队并没有成功。
顶级团队注意到的另一件有趣的事情是，ArcFace 的最佳缩放和边距参数对于图像和文本模型是不同的。 因此他们必须单独调整它们。

So, which method is State-of-the-Art?

这实际上取决于您的具体任务和数据。 到目前为止，我会推荐以下内容：

如果您没有太多数据，或者在无人监督的环境中，Triplet Loss 可能仍然是一个不错的选择。 Shopee 价格匹配保证挑战赛（2020 年）的第三名清楚地证明了这一点。
否则，在严格监督的环境中，您不会期望测试集中出现严重超出分布的样本，ArcFace 及其变体绝对是最佳选择，正如最近 Kaggle 竞赛中表现最佳的选手所证明的那样。 如果您的数据具有较大的类内变异性和稀有类的长尾，那么 Sub-Center ArcFace + Dynamic Margin 可能是您需要考虑的方法。 不要忘记使用 GeM 并遵循图 14 所示的架构。
根据任务的不同，仅靠度量学习通常是不够的。 在图像检索任务中，它通常与查询扩展、特征匹配以及其他后处理和验证方法配合使用。