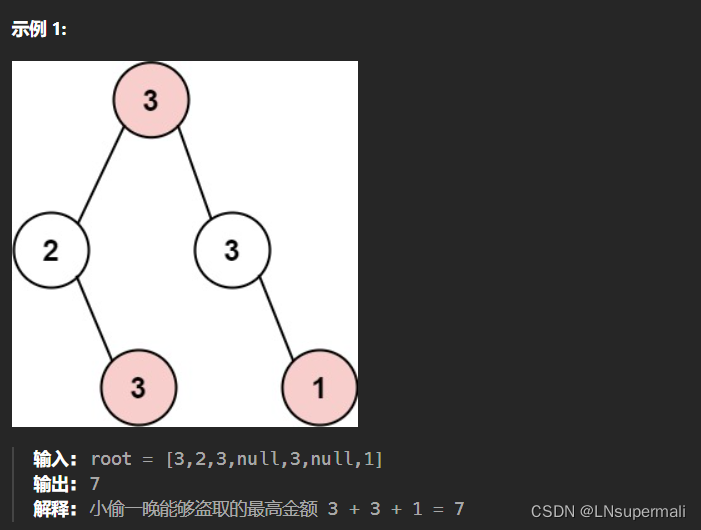
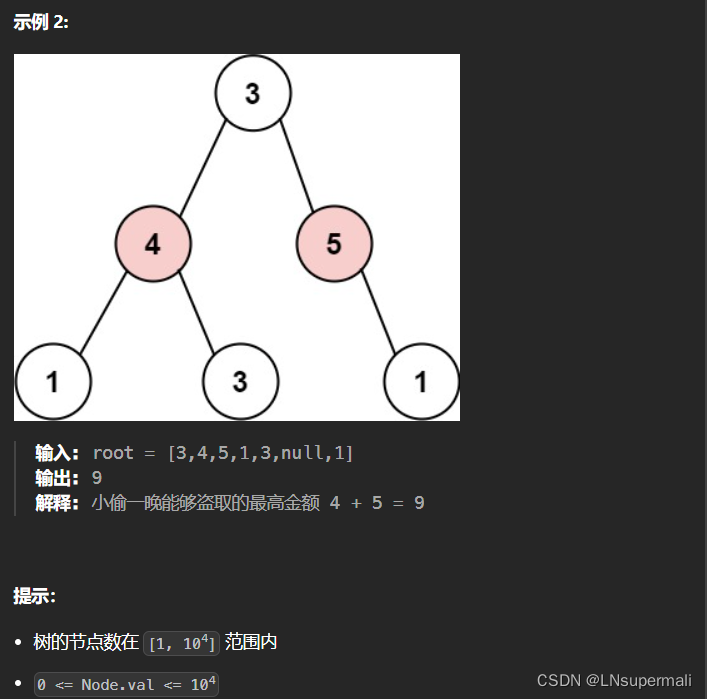
力扣337. 打家劫舍 III(java 动态规划)
Problem: 337. 打家劫舍 III
题目描述
思路
1.构建多阶段决策模型:树形DP基于树这种数据结构上的推导,一般都是从上往下推,子节点状态推导父节点状态,一般都是基于后续遍历来实现。
2.定义状态:每个节点有两个状态;偷、不偷int moeny[2]表示每个节点的状态;money[0]表示选择不偷此节点,当下最大金额,money[1]表示选择偷此节点,当下最大金额。
3.定义状态转移方程:root.money[0] = max(left.money[0], left.money[1]) + max(right.money[0], right.money[1])即表示若当前节点选择不偷,则当前可以获得的最大金额为左右子节点的可偷或则不可偷的最大金额和;root.money[1] = left.money[0] + right.money[0] + root.val; 即表示若选择偷当前的节点则当前可以获得的最大金额为当前节点左右子节点均不偷可以获得的最大金额之和再加上当前偷取的金额
解题方法
1.编写并调用int[]类型函数postorder(将其赋值给一个int[]数组名为money)
1.1若当前节点为null则返回一个int数组;
1.2递归处理:依次递归处理左子节点偷取最大金额、右子节点偷取最大金额;
1.2递归处理操作:实现上述动态转移方程。
2.返回最终数组money中的较大值max(money[0], money[1])
复杂度
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为二叉树的节点的个数
空间复杂度:
O ( l o g n ) O(logn) O(logn)
Code
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* Get the maximum amount you can steal (tree DP)
*
* @param root
* @return int
*/
public int rob(TreeNode root) {
int[] money = postorder(root);
return Math.max(money[0], money[1]);
}
/**
* The next iteration gets the maximum amount that can be stolen
*
* @param root The root node of a binary tree
* @return int[]
*/
private int[] postorder(TreeNode root) {
if (root == null) {
return new int[]{0, 0};
}
int[] leftMoney = postorder(root.left);
int[] rightMoney = postorder(root.right);
int[] money = new int[2];
money[0] = Math.max(leftMoney[0], leftMoney[1]) + Math.max(rightMoney[0], rightMoney[1]);
money[1] = (leftMoney[0] + rightMoney[0]) + root.val;
return money;
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MFC工程中无法使用cygwin64的库
- 【Mac】flutter项目集成高德定位SDK,获取key
- peropure·AI:开创智能助手新纪元
- 电阻器的 功率 电压 电流 你知道多少?
- python pydantic
- 企业中真实的软件测试的流程有哪些?都在这里了!
- Halcon基于相关性的模板匹配create_ncc_model
- 将 SQL Server 2022 数据库备份到 MinIO
- 数据分析的理念、流程、方法、工具(上)
- 学校安保项目投标标书:构建校园安全的保障