深度学习记录--指数加权平均

发布时间：2024年01月21日

指数加权移动平均(exponentially weighted moving averages)

如何对杂乱的数据进行拟合？

通过指数加权平均可以把数据图近似拟合成一条曲线

公式：
v_{t}=\beta v_{t-1}+(1-\beta)\theta_{t}

其中v_{t}表示第t个平均数，v_{t-1}表示第t-1个平均数，\theta_{t}表示第t个数据，\beta表示变化参数

下图为拟合结果(\beta=0.9)

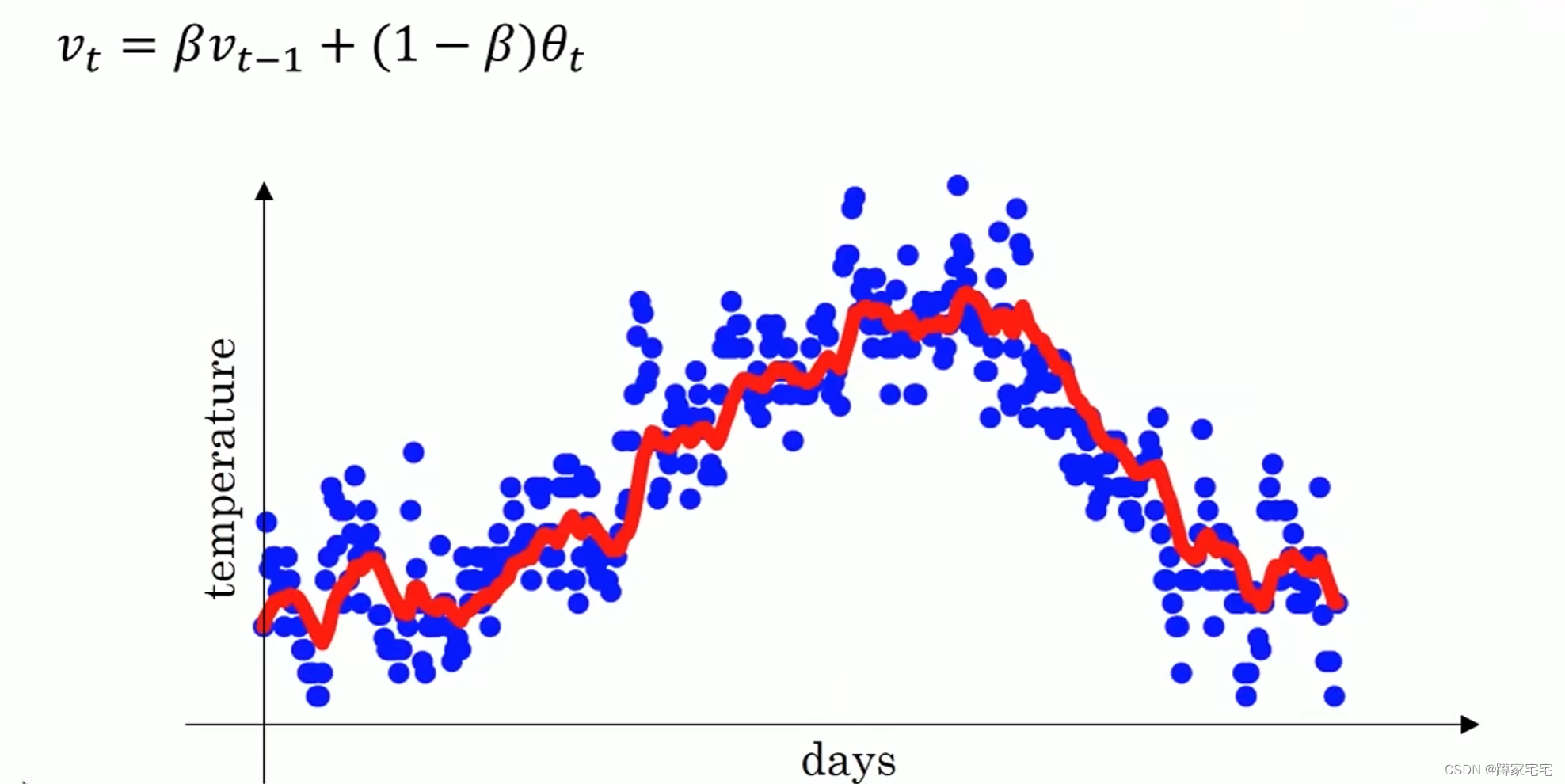
当参数\beta变化时，拟合结果也会发生变化

例子：
\beta=0.9?时，近似取10个数据平均值(红色曲线)

\beta=0.98?时，近似取50个数据平均值(绿色曲线)

\beta=0.5?时，近似取2个数据平均值(黄色曲线)

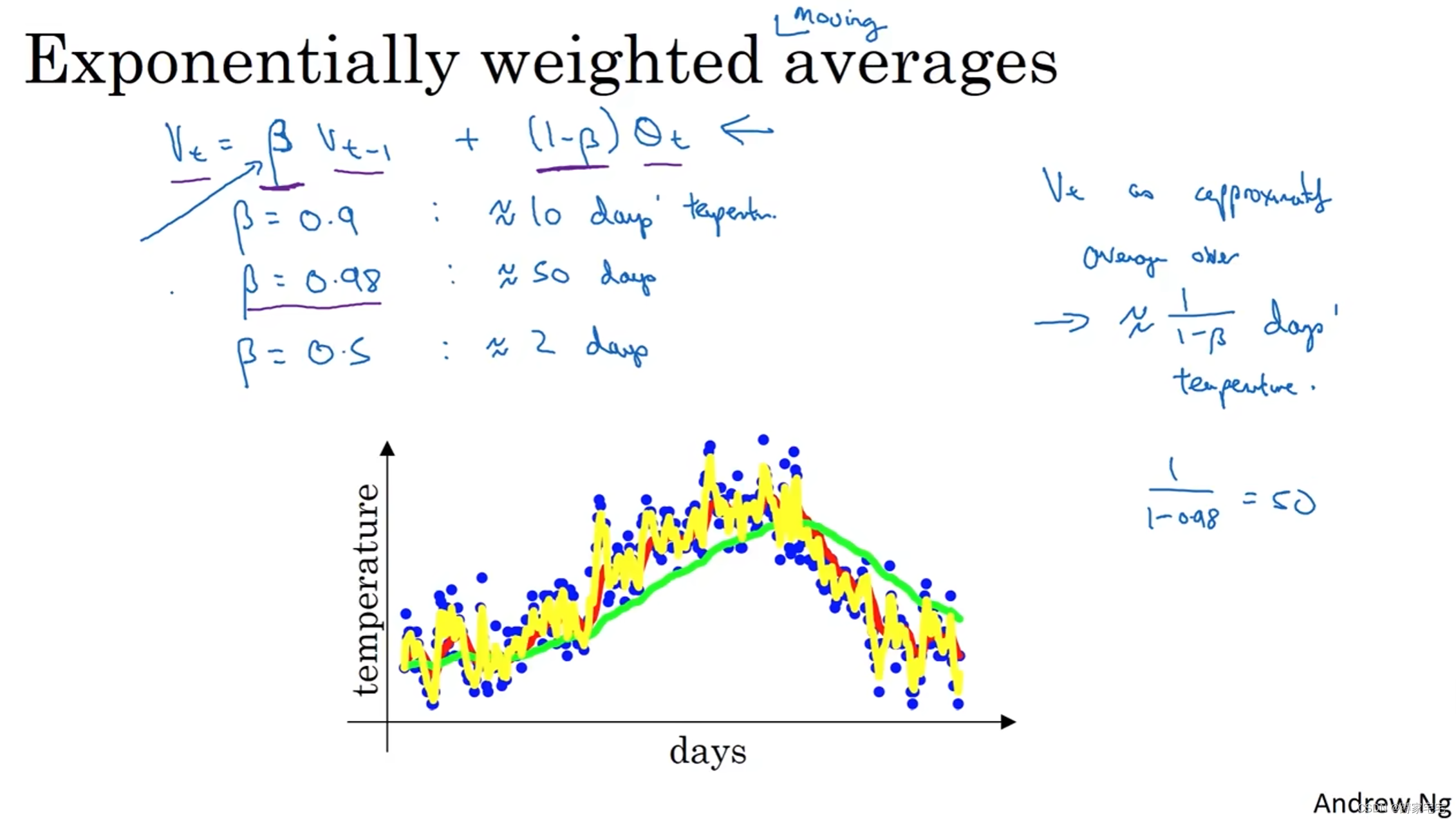
从上图三条曲线可知

参数\beta的取值对拟合结果的影响很大，那么有什么规律？

\beta较大时，拟合结果更加平稳，因为取的是更多数据的平均值

\beta较小时，拟合结果波动较大，因为取的是更少数据的平均值

公式：\frac{1}{1-\beta}

这个公式可以用来计算采样数据的数量

当\beta较大时，公式值较大，即取的更多数据的平均值

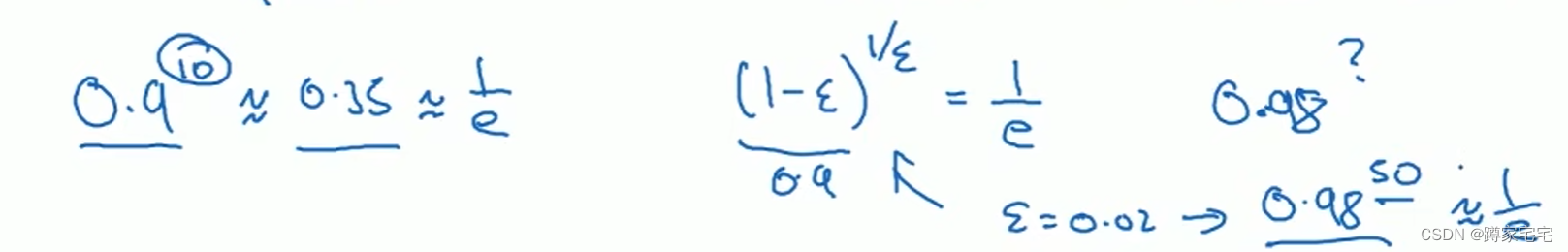
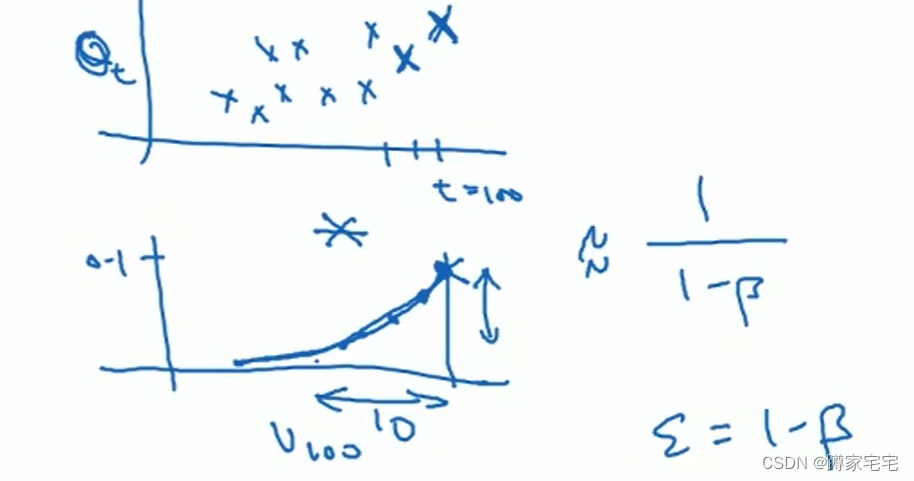
优点：
减少内存占用，只需一行代码实现重复更新

v=0
beta=0.9
theta=[1,2,4,5,6,8,10,14,18,22]
# theta[i]代表当前数据
for i in range(0,10):
    v=beta*v+(1-beta)*theta[i]
    print("v",i+1," = ",v)

偏差修正(bias correction)

当\beta较大时，初期数据拟合可能偏差较大，为了更好地拟合初期的数据，故采用偏差修正

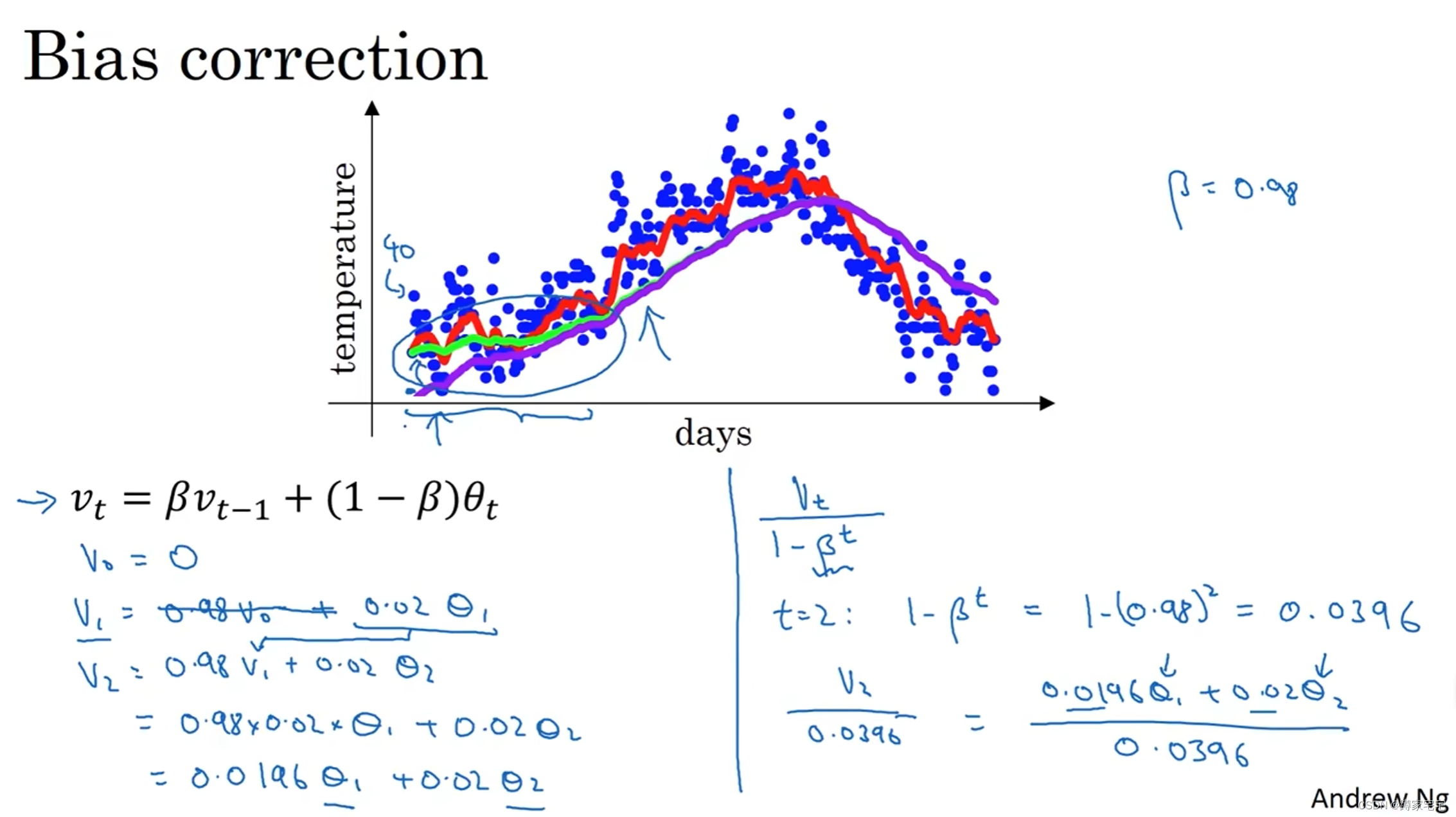
所得到的v值进行进一步的处理：

\frac{v_{t}}{1-\beta_{t}}，其中t为天数

故当t较小时，v_{t}可以被适当放大，更加拟合数据

当t变大，分母逐渐趋于1，所以后阶段偏差修正作用不大

总而言之，偏差修正是一种针对初期数据的修正偏差的方法

文章来源:https://blog.csdn.net/Xudong_12345/article/details/135707483
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章