基于强化学习的MPC模型预测控制算法仿真,并应用到车辆变道轨迹跟踪控制领域
目录
? ? ? ? ?模型预测控制(MPC)是一种优化控制方法,它通过在线解决一个有限时域内的开环最优控制问题来得到当前的控制动作。传统的MPC方法依赖于一个准确的系统模型来进行预测和优化。然而,在实际应用中,获取准确的系统模型往往是困难的。基于强化学习的MPC算法旨在通过与环境交互来学习一个模型或策略,从而实现对系统的优化控制。基于强化学习的MPC算法通常包括以下几个关键组成部分:
-
系统模型:虽然强化学习可以在没有模型的情况下工作,但在MPC的上下文中,通常还是需要一个模型来进行预测。这个模型可以是基于物理定律的,也可以是通过学习得到的。模型用于预测未来一段时间内的系统状态和控制动作。
-
优化目标:定义一个优化目标(或成本函数),该函数描述了希望系统达到的状态或行为。这个目标通常包括跟踪误差、控制努力和系统约束等项。
-
滚动优化:在每个控制时刻,MPC算法会解决一个有限时域内的开环优化问题,以找到最优的控制序列。然后,只实施该序列的第一个控制动作,并在下一个时刻重复该过程。
-
强化学习:强化学习用于改进MPC的性能。通过与环境的交互,算法学习一个策略或价值函数,该函数可以在没有显式模型的情况下指导控制动作的选择。
1.模型预测控制的基本原理
? ? ? ? 模型预测控制(MPC)从提出至今已有40余年。发展至今,MPC的原理趋于成熟,MPC的基本结构如图所示。在MPC的结构中,滚动优化模块和预测模型模块为MPC的两个核心部分。
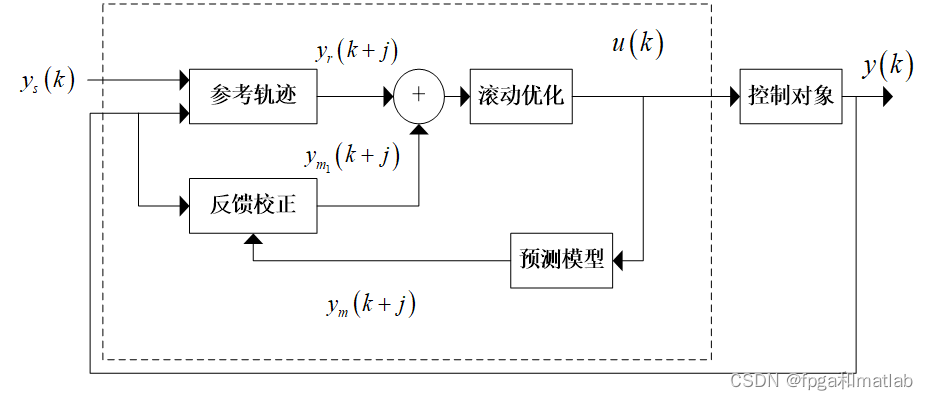
? ? ? ? 其中参考轨迹模块的主要功能是当参考输入 发生突变时,使得参考轨迹可以缓慢的接近参考输入值,从而有效防止控制器出现超调、不稳定的情况发生。常见的参考轨迹计算公式如下所示:
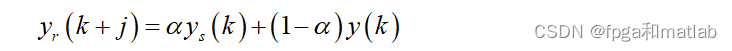
? ? ? ?预测模型主要是根据系统的控制量、状态变量、输出变量、历史数据以及未来一段时间的控制律来预测未来的输出,MPC的工作示意图如图所示。
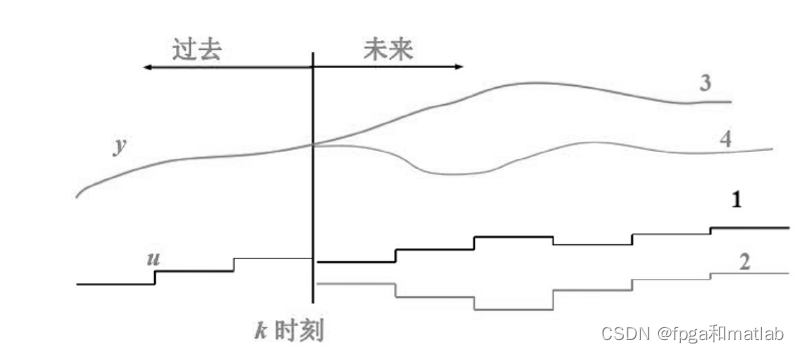
预测模型的计算表达式如下所示:
![]()
? ? ? ?滚动优化模块,其主要通过合适的优化算法来搜索最优控制律。通过不断的更新最优控制律实现滚动优化。在计算最优控制律之前,首先需要设计一个优化目标函数,通常情况下,使用预测轨迹和参考轨迹差的绝对值作为优化目标函数。此外,又由于车辆模型为一个复杂的非线性模型,因此,其表达式通常可以采用如下的二次型表达式表示所示:
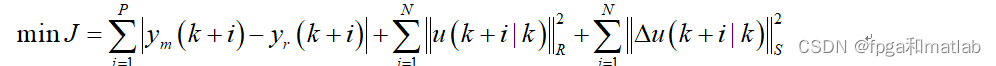
2.强化学习的基本原理
? ? ? ?强化学习(Reinforcement Learning,RL)是目前AI研究的一个重要方向[05]。强化学习算法的核心功能是通过与外部环境的交互学习,即根据环境的变化,不断的指导控制器做出最优的控制策略,使得整个系统实时的适应外部环境的变化,从而实现最佳控制效果。基于强化学习的控制器,其通过设计一个奖励函数对外部环境改变所做出的控制决策所对应的控制性能进行评价,使得系统的控制效果在当前环境状态下达到最大奖励,即最优控制效果。
? ? ? ?强化学习的基本结构如下图所示:
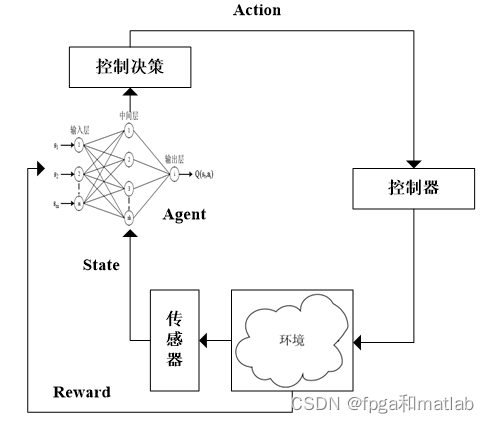
? ? ? ?从图可知,强化学习的基本结构包括一个类似神经网络学习模块的智能体(Agent),外部工作环境(environment),控制决策单元以及控制器模块。在强化学习工作过程中,Agent和environment进行交互,Agent根据知识储备做出控制策略,并给出相应的action,当环境接收到来自Agent的action之后,给出一个反应当前控制效果的奖励值reward以及环境状态state。
3.基于强化学习的模型预测控制算法
? ? ? MPC在控制过程中,其内部的预测模型 对MPC的控制性能有着决定性的作用。预测模型通过预测未来的控制序列来实现模型预测控制,但其极易受到外部干扰因素影响,因此传统的预测模型如ARIMA模型,BP神经网络模型等无法满足实际控制需求,且算法复杂度较高。而强化学习具备与外部环境的交互学习能力,使得基于强化学习的MPC预测模型具备更加精确的预测效果,并具备实时反映外部客观环境的能力。
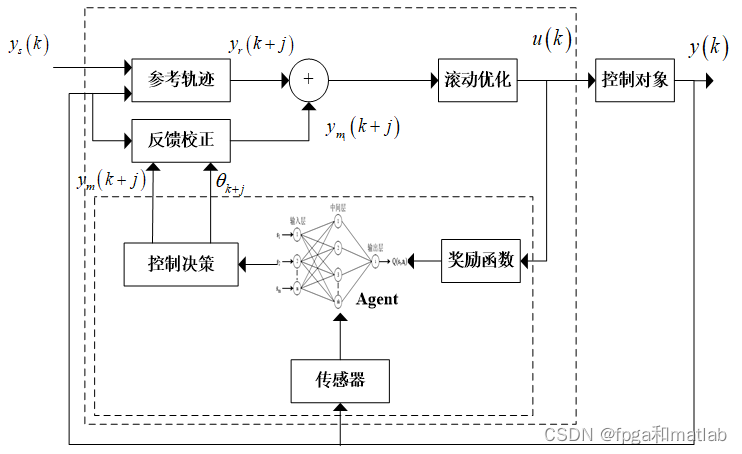
4.Simulink建模与matlab编程
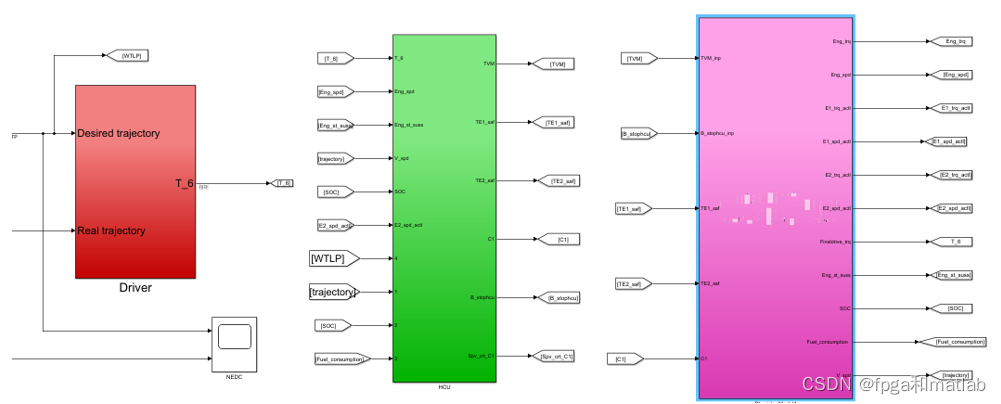
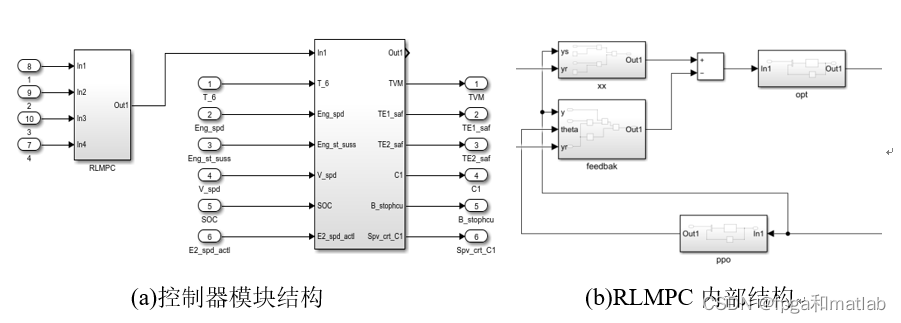
...............................................................
for iter_out=1:EP_MAX
iter_out
count = 0;
failure = 0;
iter_in = 1;
if iter_out==1
nstate = IState;
end
inputs = nstate./Vbase;
lc = C_LR;
la = A_LR;
xhist = nstate;
%计算新的操作ACTION
ha = inputs*wa1;
gs = (1 - exp(-ha))./(1 + exp(-ha));
va = gs*wa2;
newAction = (1 - exp(-va))./(1 + exp(-va));
%计算J
inp = [inputs newAction];
qc = inp*wc1;
p = (1 - exp(-qc))./(1 + exp(-qc));
J = p*wc2;
Jold = J;
%内循环
tmpss = 0;
Vs = 0;
while(iter_in<EP_LEN)
%设置环境随机变化因子
Seeds = iter_in;
%根据新产生的操作指令,产生对应的PID校正信号
if newAction >= 0
K=K+1;
else
K=K-1;
end
dp1 = dp1*(K/EP_LEN);
dp2 = dp2*(K/EP_LEN);
dp3 = dp3*(K/EP_LEN);
dp4 = dp4*(K/EP_LEN);
dp5 = dp5*(K/EP_LEN);
dp6 = dp6*(K/EP_LEN);
%%
%对模型进行训练,作为环境模型交互使用
sim('tops.mdl');
p_ = mean(E.signals(1).values);
q_ = mean(E.signals(2).values);
r_ = mean(E.signals(3).values);
fai_ = mean(F.signals(1).values);
theta_= mean(F.signals(2).values);
psi_ = mean(F.signals(3).values);
roll_ = mean(A.signals(1).values);
pitch_= mean(A.signals(2).values);
yaw_ = mean(A.signals(3).values);
nstate = [p_-xdes,q_-ydes,r_-zdes,fai_,theta_,psi_]./Vbase;
inputs = nstate./Vbase;
%PPO
ppo();
reward = 5e-3*sqrt(abs(p_^2 + q_^2 + r_^2))+...
2e-3*sqrt(abs(fai_^2 + theta_^2 + psi_^2))+...
8e-3*sqrt(abs(roll_^2 + pitch_^2 + yaw_^2));
%过大过小切断
if reward > 0.03
reward = 0.03;
end
if reward < 0
reward = 0;
end
%%
%update critic网络
critic_nn();
%%
%update actor 网络
actor_nn();
iter_in = iter_in+1;
if rand<min(iter_out*confidence/200,confidence)
Vs = reward + GAMMA * Vs;
tmpss = tmpss + reward;
else
tmpss = tmpss;
end
end
if tmpss > 100
failure = 0;
else
failure = 1;
end
%更新
if iter_out~=EP_MAX
for s=1:wrongstore-1
wrongstate(s,:) = wrongstate(s+1,:);
end
wrongstate(wrongstore,:) = [iter_in,0];
for i=1:wrongstore-1
if abs(wrongstate(i,1)-wrongstate(i+1,1))<=5
count=count+1;
end
end
if count==wrongcnt
wc1=(rand(N_wci,N_Hidden)-0.5)*beta2;
wc2=(rand(N_Hidden,1)-0.5)*beta2;
wa1=(rand(N_wai,N_Hidden)-0.5)*beta2;
wa2=(rand(N_Hidden,1)-0.5)*beta2;
end
end
Nreward(iter_out)=tmpss/EP_LEN;
dp1_(iter_out) = dp1;
dp2_(iter_out) = dp2;
dp3_(iter_out) = dp3;
dp4_(iter_out) = dp4;
dp5_(iter_out) = dp5;
dp6_(iter_out) = dp6;
end
%先归一化处理,再进行显示
% figure
% plot(Nreward,'b-*');
% ylabel('Reward');
% xlabel('episode');
% grid on
up4020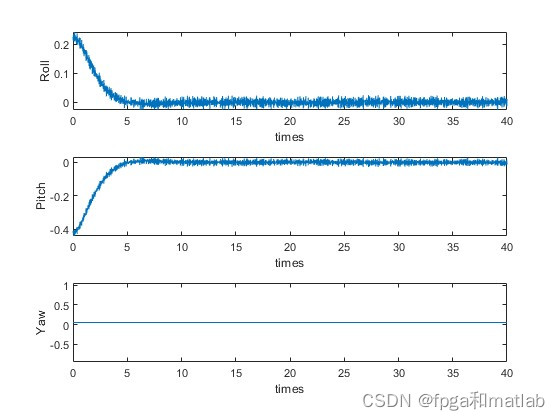
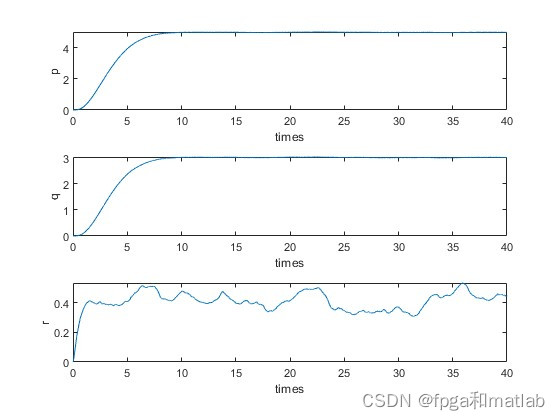
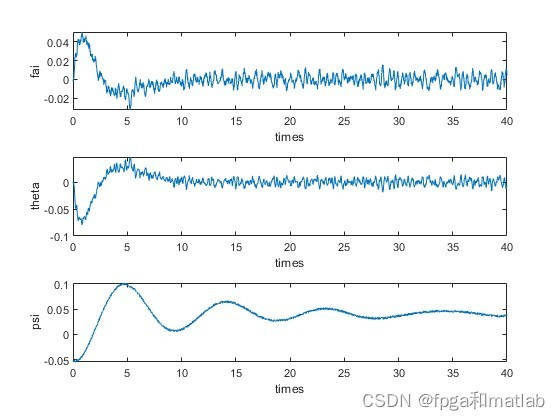
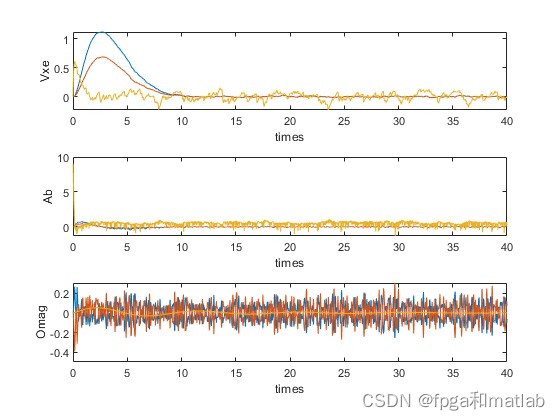
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- leetcode
- Vue关于Vuex实现组件中数据的共享要点总结和部分代码
- CentOS Stream 9配置yum源
- 自动化测试|Eolink Apikit 如何保存、使用测试用例
- 解决Windows 11/10共享打印机无法连接问题0x00000709错误
- kubernetes 灰度发布设计方案
- M-G370PDF1(IMU)
- spring基于注解的事务管理器自动配置实现分析
- 宝塔面板怎么安装指定版本redis_宝塔redis安装5.0版本
- “/bin/bash“: stat /bin/bash: no such file or directory: unknown