Python - 深夜数据结构与算法之 DP - 进阶

目录

一.引言

二.经典算法实战

1.House-Robber [198]

2.House-Robber-2 [213]

3.Best-Sell-Time [121]

4.Best-Sell-Time-2 [122]

5.Best-Sell-Time-3 [123]

6.Best-Sell-Time-4 [188]

7.Best-Sell-Time-Coldown [309]

8. Best-Sell-Time-Fee [714]

三.总结

---

一.引言

前面我们介绍了一部分 DP 动态规划的题目，由于动态规划在算法中算是一大难点，所以我们接下来继续讲解动态规划的相关算法题目。

二.经典算法实战

1.House-Robber [198]

打家劫舍:?https://leetcode.cn/problems/house-robber/description/

◆ 题目分析

0-不偷 1-偷

a[i][0] = max(a[i-1][0], a[i-1][1])

a[i][1] = a[i-1][0] + nums[i]

即对于每一个位置 i，其存在两种可能，偷和不偷。如果偷 i，则 a[i-1] 不能偷，所以就是 a[i-1][0]，如果不偷 i，则 a[i-1] 可以偷也可以不偷，所以是 max(a[i-1][0], a[i-1][1])。

◆ 动态规划 V1

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        
        dp = []
        for i in range(len(nums)):
            dp.append([0, 0])

        # 初始化状态
        dp[0][0] = 0
        dp[0][1] = nums[0]

        # DP 转移
        for i in range(1, len(nums)):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1])
            dp[i][1] = dp[i - 1][0] + nums[i]
        
        return max(dp[-1][0], dp[-1][1])

◆ 动态规划 V2

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if len(nums) == 0: return 0
        if len(nums) == 1: return nums[0]

        N = len(nums)
        dp = [0] * (N+1)
        dp[0] = nums[0]
        dp[1] = max(nums[0], nums[1])
        for i in range(2, N):
            # 对于第K个房子，要么 [k-1 房子偷，K不偷] 要么 [k-1 不偷，那就是 k-2 的值 + nums[k]]
            dp[i] = max(dp[i-1], dp[i-2] + nums[i])
    
        return dp[N-1]
        

上面用两个状态 [0][1] 维护，下面我们优化一下使用一个状态维护，这里 a[i] 表示当前能偷到的最大值，注意此时 a[i] 可能被偷了也可能没被偷。

◆ 动态规划 V3

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """

        # 上一个，当前值
        pre, now = 0, 0

        for i in nums:
            pre, now = now, max(pre + i, now)

        return now
        

观察上面的递推，我们使用了 o(n) 的复杂度，但其实 n 只取决于 n-1 和 n-2，所以我们可以优化为双指针。?这里运行时间受乐扣后台机器的情况而定，我们主要掌握解题的思路和代码的优化。

2.House-Robber-2 [213]

打家劫舍2:?https://leetcode.cn/problems/house-robber-ii/description/?

◆ 题目分析

与上题唯一不同是第一个房子和最后一个房子连在一起，变成环形了无法同时偷，所以可以转变思路，要么不偷第一个，则求 nums[1:] 的打家劫舍问题，要么不偷最后一个，偷 nums[: len(nums)-1] 的打家劫舍问题。

◆ 动态规划

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """

        N = len(nums)
        if N == 0:
            return 0
        if N == 1:
            return nums[0]

        # 偷第一家 不偷最后一家
        dp = nums[:N-1]

        pre, now = 0, 0
        for i in dp:
            pre, now = now, max(pre + i, now)
        
        # 偷最后一家，不偷第一家
        pre2, now2 = 0, 0
        dp2 = nums[1:]
        for i in dp2:
            pre2, now2 = now2, max(pre2 + i, now2)
        
        return max(now, now2)

边界条件加上两次打家劫舍完成。

3.Best-Sell-Time [121]

股票买卖最佳时机:?https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/?

◆ 题目分析

记录过去的最小值，然后记录 dp 状态，dp[i] = max(dp[i] - pre_min, 0)，即当前卖出能获得的最大值，如果卖了亏钱那就是 0，这里需要维护 dp 数组与 min。

◆ 动态规划 V1

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        # dp[i] = max(dp[i] - pre_min, 0)

        cur_min = prices[0]
        dp = [0] * len(prices)
        for i in range(1, len(prices)):
            dp[i] = max(prices[i] - cur_min, dp[i-1])
            cur_min = min(cur_min, prices[i])

        return dp[-1]

◆ 动态规划 V2

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        # dp[i] = max(dp[i] - pre_min, 0)

        cur_min = prices[0]
        res = 0

        for i in prices[1:]:
            res = max(i - cur_min, res)
            cur_min = min(cur_min, i)
        
        return res

上面 dp 浪费了 o(n) 的数组，其实我们只需要知道当前的最大和最小值，构造两个指针即可，比刚才好一些了。

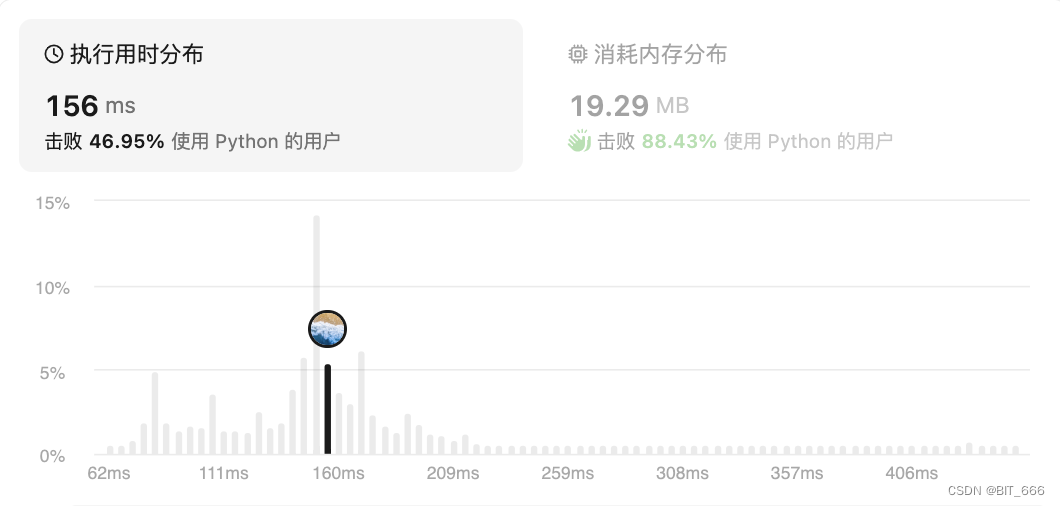
4.Best-Sell-Time-2 [122]

股票买卖最佳时机2:?https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii

◆ 题目分析

这个题目相当于上帝视角买卖股票，所以有一个贪心的策略就是只要第二天比第一天高，我们就进行一次交易获利。当然也可以使用动态规划，规划的转移方程可以描述为:

dp[i] = max(dp[i] - dp[i-1], 0) + dp[i-1]

即这次可以获得的金额是上次的加上今天买卖的值，今天买卖不了就 0。

◆ 贪心算法

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        reward = 0

        for i in range(1, len(prices)):
            reward += max(prices[i] - prices[i-1], 0)
        
        return reward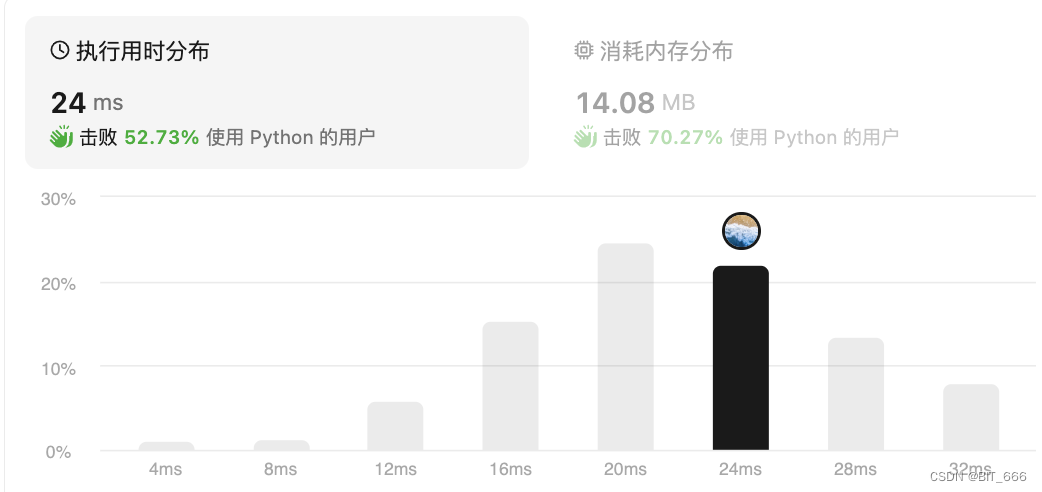

◆ 动态规划 - V1

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """

        N = len(prices)

        dp = [0] * N

        # 当前位置的收益等于上一次的收益和本次的正收益
        for i in range(1, N):
            dp[i] = max(prices[i] - prices[i-1], 0) + dp[i-1]
        
        return dp[-1]

◆ 动态规划 - V2

class Solution(object):
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        
        # 双指针
        pre = 0
        now = 0

        for i in range(1, len(prices)):
            now = max(prices[i] - prices[i-1], 0) + pre
            pre = now
        
        return now

DP 转移方程只用到上一次的状态，所以使用双指针即可。?

5.Best-Sell-Time-3 [123]

股票最佳买卖时间 3:?https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii

◆ 题目分析

前面的题目只有买与卖即两个状态，这里增加了第二次买第二次卖，所以需要增加第二次买卖。

0-无操作

1-第一次持有

2-第一次卖出

3-第二次持有

4-第二次卖出

dp[i][j] 中 i 表示第 i 天，j 为 [0 - 4] 五个状态，dp[i][j] 表示第 i 天状态 j 所剩最大现金。?

◆ 动态规划 - V1

    def maxProfit(self, prices):
        """
            0-无操作
            1-第一次持有
            2-第一次卖出
            3-第二次持有
            4-第二次卖出
            dp[i][j]中 i 表示第 i 天，j 为 [0 - 4] 五个状态，dp[i][j] 表示第 i 天状态 j 所剩最大现金。

        """
        if len(prices) == 0:
            return 0

        # 初始化 DP 空间
        dp = [[0] * 5 for _ in range(len(prices))]

        # 第一次持有需要花 -p 的钱
        dp[0][1] = -prices[0]
        # 第二次持有因为是买了卖再买，所以还是 -p
        dp[0][3] = -prices[0]

        for i in range(1, len(prices)):
            # 无操作
            dp[i][0] = dp[i - 1][0]
            # 第一天买入股票，要么是之前的股票还在即 dp[i-1][1] 要么是 i-1 没买，现在买即 dp[i-1][0] - p
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
            # 第一天卖出股票，要么是之前已经买了即 dp[i-1][2] 要么是 i-1 买了，i 卖了，所以 dp[i-1][1] + p
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i])
            # 第二天买入同理
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i])
            # 第二天卖出同理
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i])
        return dp[-1][4]

对于买卖而言，都有两种状态，一种是维护现状，一种是买卖，这里逻辑比较混乱，还得多理理。

◆ 动态规划 - V2?

class Solution(object):
    def maxProfit(self, prices):
        # 买入的低价
        buy_1, buy_2 = 2147483647, 2147483647
        # 收益的高点
        pro_1, pro_2 = 0, 0

        for p in prices:
            buy_1 = min(buy_1, p)
            pro_1 = max(pro_1, p - buy_1)

            buy_2 = min(buy_2, p - pro_1)
            pro_2 = max(pro_2, p - buy_2)

        return pro_2

有点像条件概率的感觉，第二次买卖是在第一次买卖发生的情况下计算的。由于第一次买卖会赚一些钱 pro1，那第二次买的时候就花费的钱就是当前价格减去咱们第一次赚的钱，price2 - pro1， 这样一来，第二次买卖的结果就代表了前两次买卖的总利润，我们求总利润的最大值就可以了。?这个思路真的牛，清晰明了，和大神还是有差距，努力学习 ing ...

6.Best-Sell-Time-4 [188]

股票买卖4:?https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/

◆ 题目分析

这里和 123 题的区别是卖 2 次和卖 n 次，通过 for 循环实现多次买卖。

◆ 动态规划 ?

class Solution(object):
    def maxProfit(self, k, prices):
        """
        :type k: int
        :type prices: List[int]
        :rtype: int
        """

        k = min(k, len(prices) // 2)

        buy = [-float("inf")] * (k+1)
        sell = [0] * (k+1)

        for p in prices:
            for i in range(1, k+1):
                buy[i] = max(buy[i], sell[i-1] - p)
                sell[i] = max(sell[i], buy[i] + p)

        return sell[-1]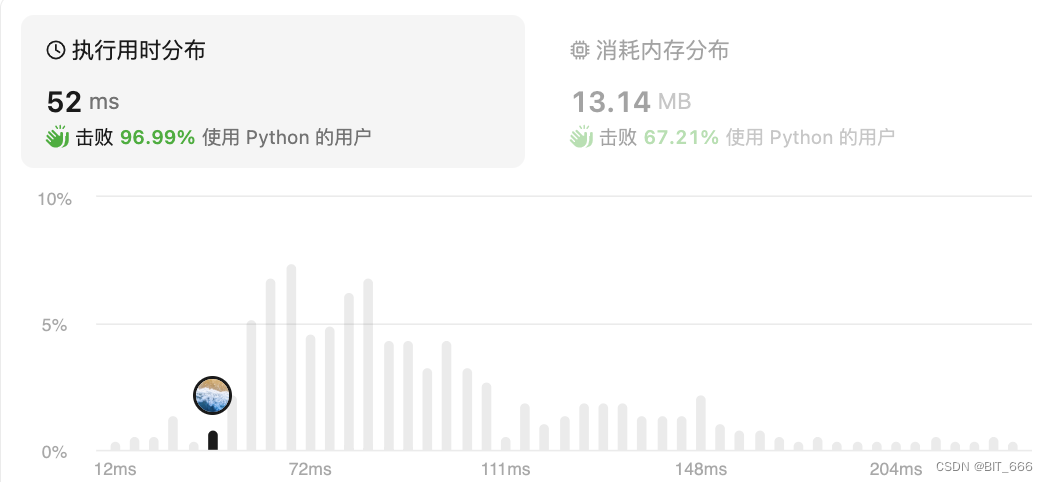

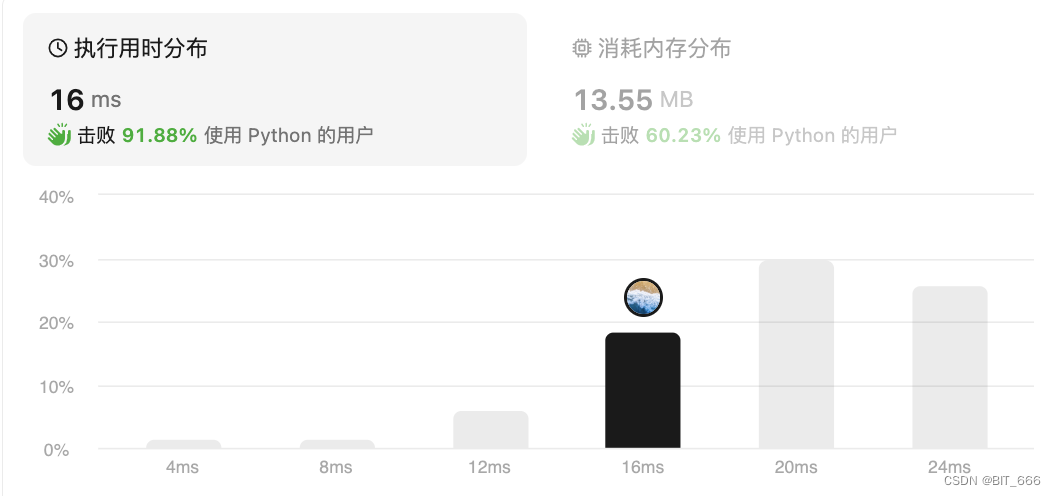
7.Best-Sell-Time-Coldown [309]

股票买卖时机-冷冻:?https://leetcode-cn.com/best-time-to-buy-and-sell-stock-with-cooldown/?

◆ 题目分析

官方题解写的比较清晰，这里做一次大自然的搬运工。

◆ 动态规划

class Solution(object):
    def maxProfit(self, prices):
        
        """
            0 - 目前有一只股票对应的最大收益
            1 - 目前没有股票，处于冷冻期的最大收益
            2 - 目前没有股票，不处于冷冻期

        """

        N = len(prices)
        dp = [[0] * 3 for _ in range(N)]
        dp[0][0] = -prices[0]
        dp[0][1], dp[0][2] = 0, 0

        for i in range(1, N):
            # 第 i 天有一只股票: A.还拿着上一天的股票 dp[i-1][0] B.昨天没股票且能买 dp[i-1][2] - price
            dp[i][0] = max(dp[i-1][0], dp[i-1][2] - prices[i])
            # 第 i 天处于冷冻期 A.i-1天卖股票了 说明 i-1 天手里必须有股票 -> dp[i-1][0] + price
            dp[i][1] = dp[i-1][0] + prices[i]
            # 第 i 天没股票且非冷冻期 A.昨天也没股票也非冷冻 dp[i-1][2] B.昨天没股票冷冻 dp[i-1][1]
            dp[i][2] = max(dp[i-1][2], dp[i-1][1])
        
        return max(dp[-1])

最后比较时，如果手上还拿着股票即 dp[i][0] 其实是亏得，因为我们没卖钱还花了买股票的钱，所以我们可以只比较 [1]、[2] 的情况即可。?

8. Best-Sell-Time-Fee [714]

股票买卖-手续费:?https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-fee/

◆ 题目分析

可以继续套用 [188] 题的思路，只不过每次卖出时增加 fee。

◆ 动态规划

class Solution:
    def maxProfit(self, prices, fee):

        buy, sell = -float("inf"), 0

        for p in prices:
            buy = max(buy, sell - p - fee)
            sell = max(sell, buy + p)
        
        return sell

三.总结

这一节我们把经典的买卖股票的问题遍历了一遍，主要思路分为两种，一种是遍历所有状态的 dp，例如可以买卖 2 次，则状态有 0123，以此类推。还有固定指针数量，每次直观增减的优化内存方法，这里题目思路很多，博主在 leetcode 上找了两种思路的整理版，上面的题目我们可以感受一下大致的思路，完整的详解可以到下面的讲解学习。

DP 转移:?DP 状态转移股票算法全解

指针循环:?指针循环股票算法全解