单调栈练习（四）— 统计全 1 子矩形

题目
同样的LeetCode原题：题目链接

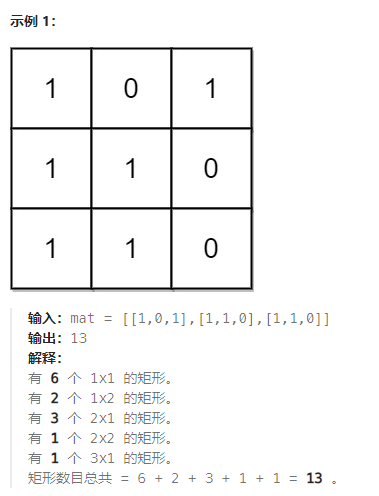
给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

单调栈
解题思路整体和上一篇文章差不多，都是用到了压缩数组的技巧，通过压缩数组来构建一个数组矩阵、以每一行为底， 每一列作为矩阵的高度，区别在于上一篇帖子是计算求矩阵的最大面积矩阵面积。而这道题是统计所有子矩阵个数。

所以这道题的区别在于，当遍历压缩数组时，以栈中弹出栈顶元素（cur）作为矩阵的高，并找到左右最近且小的值作为边界后。还要找到左右最近且小的值中的较大值（max）作为限制。只求 max ~ cur中的子矩阵的数量。

以下图为例，当前弹出的数组下标6的元素，高为6，左侧最近且小的值是在数组下标为3、高为3的值，右侧最近且小是在数组下标为9、高为4的值。

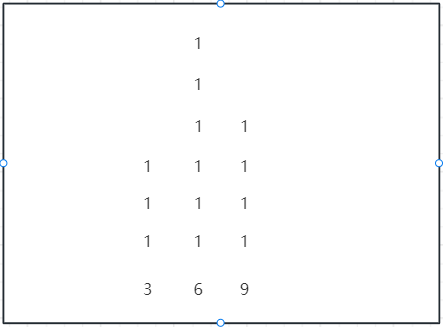
我们想求的是什么？
数组下标 4 ~ 8范围内。高度为5的子矩阵有多少， 高度为6的子矩阵有多少？也就是说，因为左右边界里，数组下标9的高度4 > 数组下标3的高度3。所以我们以4作为一个限制条件，只求范围内 > 4的子矩阵的个数。
其余 <= 4 那部分的子矩阵，等到下标9的元素弹出来时再算，这样算不会重复！！！
那4 ~ 8 范围内以5、6为高的子矩阵有多少？
一共有这些：（9 - 3） * （9 - 3 - 1） / 2 = 15

代码

public static int numSubmat(int[][] mat) {
        if (mat == null || mat[0].length == 0) {
            return 0;
        }

        int N = mat.length;
        int M = mat[0].length;
        int[] helpArr = new int[M];
        Integer sum = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                helpArr[j] = mat[i][j] == 0 ? 0 : helpArr[j] + 1;
            }
            sum += countFromBottom(helpArr);
        }
        return sum;
    }

    public static int countFromBottom(int[] height) {
        Stack<Integer> stack = new Stack<>();
        Integer sum = 0;

        for (int i = 0; i < height.length; i++) {
            while (!stack.isEmpty() && height[i] < height[stack.peek()]) {
                Integer cur = stack.pop();
                Integer leftMinIndex = stack.isEmpty() ? -1 : stack.peek();
                int n = i - leftMinIndex - 1;
                int max = Math.max(leftMinIndex == -1 ? 0 : height[leftMinIndex], height[i]);
                sum += (height[cur] - max) * num(n);
            }
            stack.push(i);
        }

        while (!stack.isEmpty()) {
            Integer cur = stack.pop();
            Integer leftMinIndex = stack.isEmpty() ? -1 : stack.peek();
            int n = height.length - leftMinIndex - 1;
            sum += (height[cur] - (leftMinIndex == -1 ? 0 : height[leftMinIndex])) * num(n);
        }
        return sum;
    }

    public static int num(int n) {
        return ((n * (1 + n)) >> 1);
    }