算法训练day51｜动态规划part12

309.最佳买卖股票时机含冷冻期（参考：代码随想录

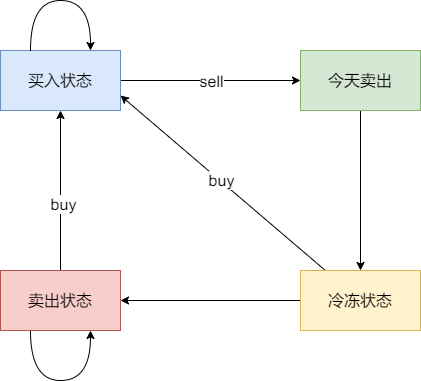
四种状态，来代表寒冷冻期的买卖股票状态?

• 状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
• 不持有股票状态，这里就有两种卖出股票状态
  • 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
  • 状态三：今天卖出股票
• 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

递推公式

达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

• 操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
• 操作二：今天买入了，有两种情况
  • 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
  • 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]

那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

• 操作一：前一天就是状态二
• 操作二：前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][3] = dp[i - 1][2];

2. 初始化

这里主要讨论一下第0天如何初始化。

如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。

保持卖出股票状态（状态二），这里其实从 「状态二」的定义来说 ，很难明确应该初始多少，这种情况我们就看递推公式需要我们给他初始成什么数值。

如果i为1，第1天买入股票，那么递归公式中需要计算 dp[i - 1][1] - prices[i] ，即 dp[0][1] - prices[1]，那么大家感受一下 dp[0][1] （即第0天的状态二）应该初始成多少，只能初始为0。想一想如果初始为其他数值，是我们第1天买入股票后 手里还剩的现金数量是不是就不对了。

今天卖出了股票（状态三），同上分析，dp[0][2]初始化为0，dp[0][3]也初始为0。

其实状态2和4可以合并

只要再次买入买入之前必须有一天的缓冲值即可，所以have stock 状态有买入更新的时候，对应的i-1th don't have stock状态，而i-1th don't have stock 状态最短时间内对应的是i-2th have stock状态，那么i-1th 就是cooldown 的时候（或者维持他自己，说明早已度过cooldown）

dp[i][0]= Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);//have stock
dp[i][1]= Math.max(dp[i-1][2],dp[i-1][1]);//don't have stock
dp[i][2] = dp[i-1][0]+prices[i]; //sell

714.买卖股票的最佳时机含手续费

知识买卖股票的dp方法多了一个手续费要考虑，买入/卖出的时候挑一处考虑手续费就可以了