推荐系统算法 协同过滤算法详解（二）皮尔森相关系数

目录

前言

协同过滤算法(简称CF)

皮尔森(pearson)相关系数公式

算法介绍

?算法示例1：

算法示例2

---

前言

理解吧同胞们，实在是没办发把wps公式复制到文章上，只能截图了，我服了！！！

协同过滤算法(简称CF)

在早期，协同过滤几乎等同于推荐系统。主要的功能是预测和推荐。协同过滤推荐算法分为两类，分别是：

（英文userCF）

1. 基于用户的协同过滤算法(相似的用户可能喜欢相同物品)；这个一般适合推荐新闻和皮皮虾之类的，数据跟人有很大关系，而且信息是每日都是更新的。如果你推荐购物这种，因为一个新建的用户可能购买的商品不足全量商品万分之1，商品数据量大，人对商品购买少，很难找到相似的人；随着用户和物品数量的增加，计算复杂度增加，所以需要这种更适合第二种算法。

（英文itemCF）

1. 基于物品的协同过滤算法（这种方法通过分析物品之间的相似性，推荐与用户之前喜欢的物品相似的其他物品）。当然也有缺点:需要足够的用户-物品交互数据来找出物品之间的相似性。

当然你除此之外，还有基于模型的协同过滤方法。这就属于更高级的推荐了，他一般是多因素，也是现代化推荐系统的主力。

• 利用机器学习算法（如矩阵分解、深度学习等）来预测用户对物品的评分或偏好。
• 优点：能够处理大规模数据集，提高推荐质量。
• 缺点：模型训练可能需要大量计算资源。

上一章讲 协同过滤算法详解（一）过了下杰卡德相似度?和 余弦相似度，如果跳不进去，直接在我的博客搜索

推荐系统算法 协同过滤算法详解（一）杰卡德相似度和余弦相似度使用、缺陷-CSDN博客

这两者都是衡量相似度的方法，但它们通常不直接被称为协同过滤算法。不过，它们可以用于协同过滤算法中计算用户或物品之间的相似度。下面讲重点了。

皮尔森(pearson)相关系数公式

????????余弦相似度的优化版本就是皮尔森相关系数（通过使用用户平均分对独立评分进行修正，减少了用户评分偏移设置的影响），两个相似度比较其实就是两条线，这两个都是通过计算三角的度数来判断相似度。当然还有个欧氏距离，这个是两边之间的距离的如果距离越长则相似度越低。

????????欧氏距离适合做活跃度那这种，因为此时，你不是去看两条线比例和夹角，两个线还是要看红线距离

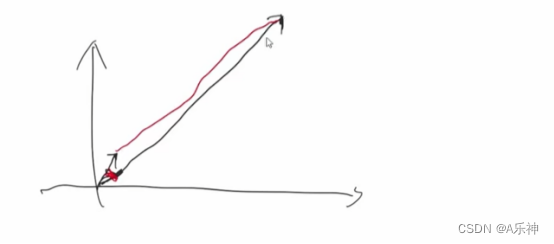
算法介绍

皮尔森(pearson)相关系数是一个结果介于-1(相反行为)和1之间的数值，绝对值越大表明相关性越强。

相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关

0到-1 负相关

但是有一个明显的缺陷就是，它只对线性关系敏感。如果关系是非线性的，哪怕两个变量之间是一一对应的关系，皮尔森相关系数也可能接近0。

事实上，皮尔森相关系数有几种不同的计算公式，它们在数学上是等价的，但形式上略有不同。这可能导致在不同情境下使用不同的公式。

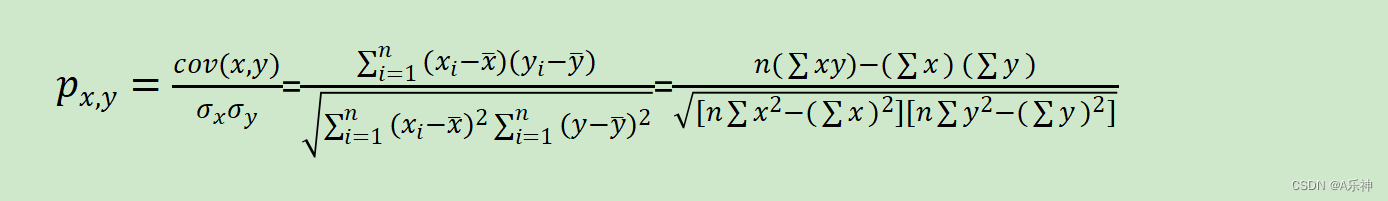
这次主要说下面常用的两种，

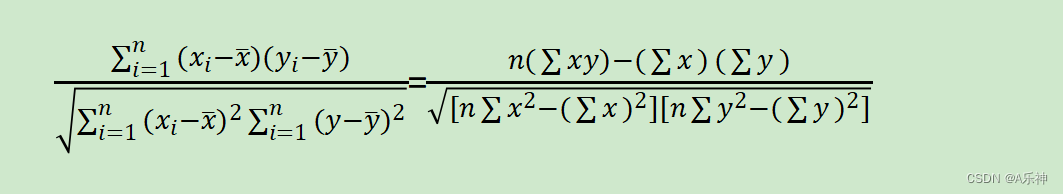
????????两个公式在数学上是等价的，它们都衡量的是两个变量之间的线性关联程度。选择哪个公式取决于具体的计算需求和可用数据。例如，在使用计算机或统计软件时，第一个公式可能更常用，因为计算均值是很直接的。而在手动计算或当有全部数据且数据量不大时，第二个公式可能更方便。

?算法示例1：

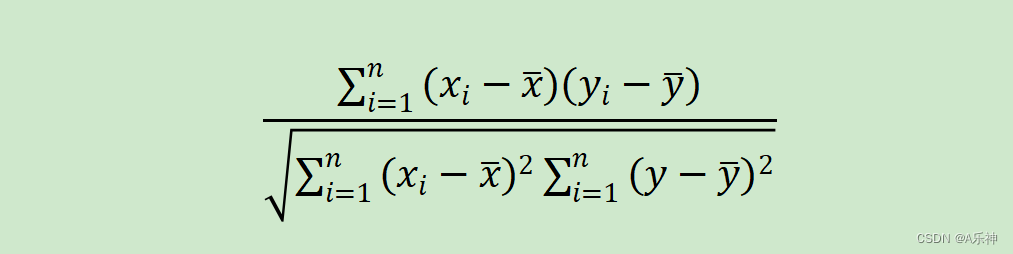
????????以下图表为例进行两个推荐，下图是个商品购买评分表，user_id是用户编号，good_id是商品编号，score是评分（范围是1-5分）

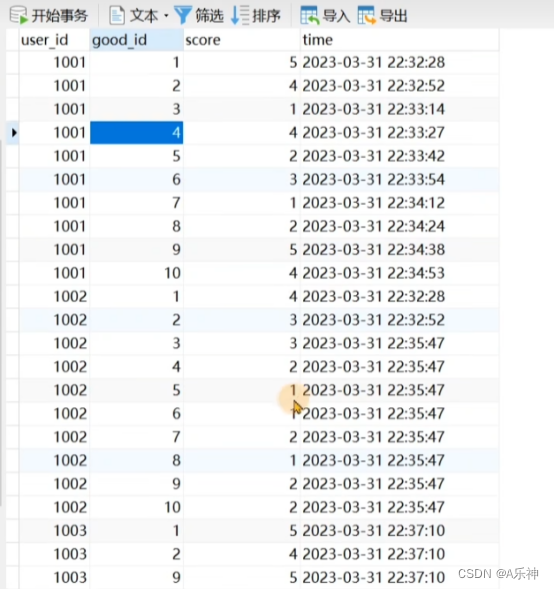
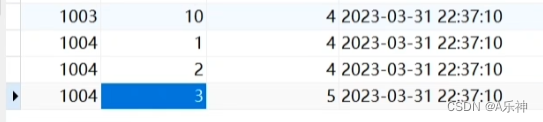
1002和1003的皮尔森系数

求：x为user_id是1003用户，y是user_id是1002用户，求二者皮尔森系数。

分子部分：

解:

?xy相同购买过商品id是1、2、9、10，列出1、2、9、10商品分数

????????x={5,4,5,4}

????????y={4,3,2,2}

x相加总分是18，则平均分是4.5，y的商品id是1、2、9、10相加是11，平均分是2.75。

=（5-4.5）(4-2.75)+（4-4.5）(3-2.75)+（5-4.5）(2-2.75)+（4-4.5）(2-2.75)

=0.5*1.25 -0.5*0.25-0.5*0.75+0.5*0.75

=0.625-0.125-0.375+0.375

=0.5

分母部分:

解:

结果：

????????0.5/1.66 =0.301

????????上述也会算出1001和1003的皮尔森系数是1，那么相对于0.3如果要推荐就推荐1001,1001内1003没有的商品就是要推荐的商品。

算法示例2

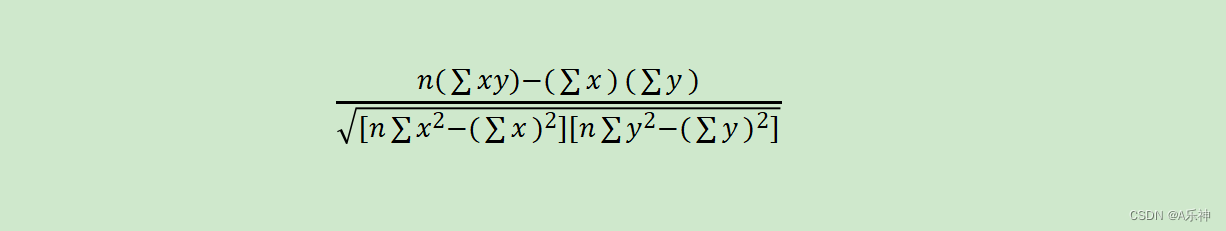
我们有两个变量 X 和 Y，每个变量有 5 个观察值：

X = {1, 2, 3, 4, 5}

Y = {2, 4, 5, 4, 5}

其中，n 是观察值的数量，x 和 y 是观察值，而 Σ 表示求和。

让我们一步一步计算：

• Σx = 1 + 2 + 3 + 4 + 5 = 15
• Σy = 2 + 4 + 5 + 4 + 5 = 20
• Σxy = 1×2 + 2×4 + 3×5 + 4×4 + 5×5 = 2 + 8 + 15 + 16 + 25 = 66
• Σx2 = 12 + 22 + 32 + 42 + 52 = 1 + 4 + 9 + 16 + 25 = 55
• Σy2 = 22 + 42 + 52 + 42 + 52 = 4 + 16 + 25 + 16 + 25 = 86
• n = 5

所以，这两组数据的皮尔森相关系数大约是 0.7746，表明它们之间存在较强的正相关关系。

------------------------------------------与正文内容无关------------------------------------
如果觉的文章写对各位读者老爷们有帮助的话，麻烦点赞加关注呗！作者在这拜谢了!

混口饭吃了！如果你需要Java 、Python毕设、商务合作、技术交流、就业指导、技术支持度过试用期。请在关注私信我，本人看到一定马上回复！