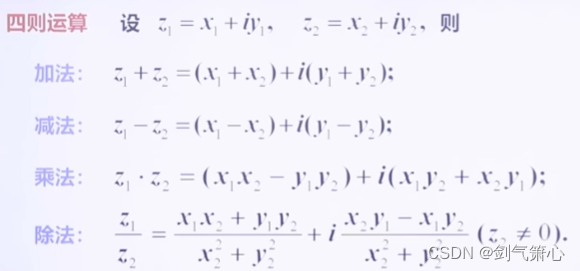复变函数与积分变换之第一章第一节：复数及其代数运算

笔者是电子信息工程在读大二学生，在大二第一学期学习了这门课程，起初自己还能好好坚持，后来越来越放纵自己，感觉一度失去了很多机会。后面打算自学《信号与线性系统》，翻开书后发现很多东西都是复变函数的基础，因此我决定利用寒假，重新来过!*如果你是第一次学习复变函数与积分变换，我劝你一定要好好学。电子信息大类都离不开这门课程，可以说这门课程是极其重要的一门数理基础课，而且这门课本身难度不小！

?*本课程是基于华中科技大学李红教授主编的《复变函数与积分变换》以及长安大学冯复科教授主编的《复变函数与积分变换》。笔者将结合自身学习经历，把重点内容总结出来供大家参考。*此系列文章是面向应用的，因此不会深究数学推导。故本文不偏向于没有基础的人学习。

本课程思维导图：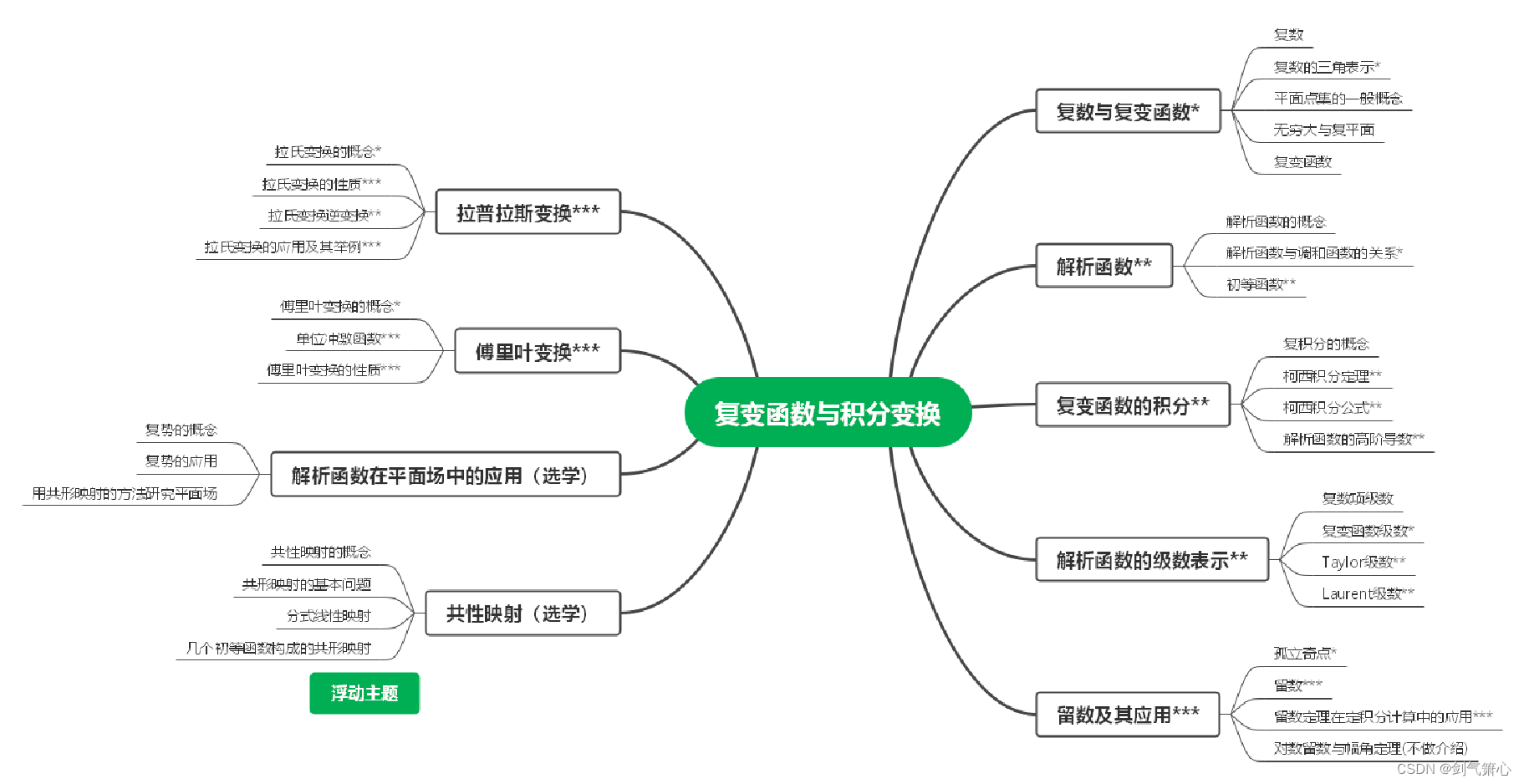

*越多，越重要。

今天我们介绍第一章：复数与复变函数。

?一.复数及其代数运算

(一)复数的基本概念?

注意：两个复数无法直接比较大小！除非它们的虚部都为0。

eg.i > 0 (×)

(二)复数的四则运算

1.复数的四则运算

***一定要注意，除法中分母不为零；（可能你会觉得这不是在说废话吗？哈哈哈，表面看上去确实如此，但请你想想如何判断分母为零的情况呢？注意：只能用判断模长不为零或实部和虚部同时为零的方法，通常我们采用第一种。）

*复数的加法和乘法运算满足交换律、结合律以及乘法对加法的分配律。

2.复数的共轭

*第三条性质在后边介绍到复数的模长时还会出现。请参考复数的表示方法之向量表示法中模长的概念，你会发现：1.互为共轭的复数模长相等。

2.复数模长的平方等于共轭复数之积。

*图片中的几条性质在后续做题过程中常常用到，尤其是出现在一些证明题中。

(三)复数的表示方法

复数的表示方法有六种，以下我们一一介绍（*这里的学习难度在于如何更好地把实数域中的概念和复数域结合起来）

1.笛卡尔坐标表示法

z = x+ iy

2.点表示法

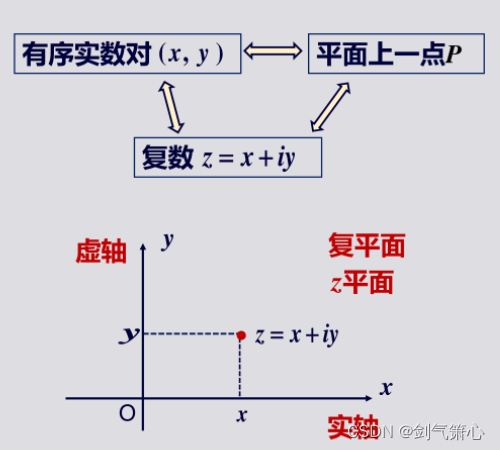
3.向量表示法

（1）表示方法

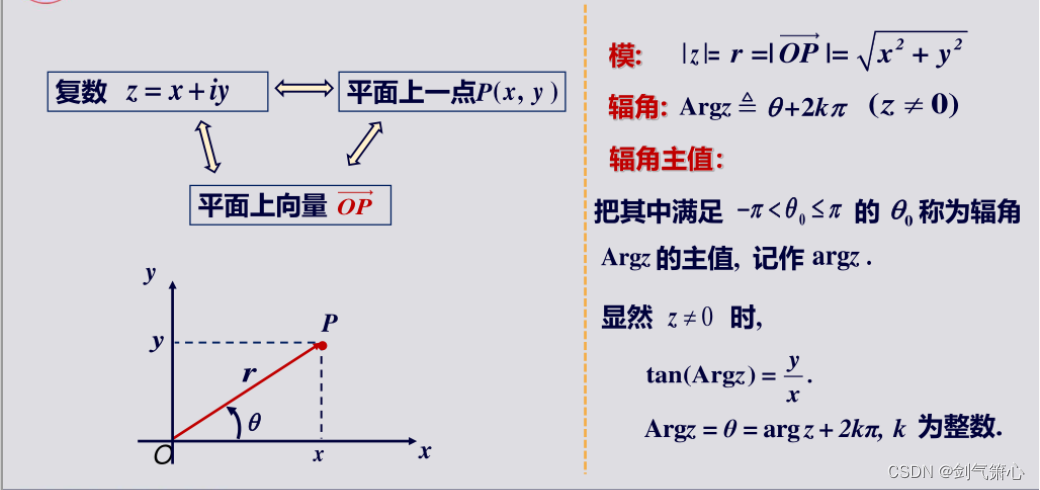
*辐角主值取值范围具有左开右闭的性质

*密切关注辐角和辐角主值之间的关系！这点很重要！

(2)辐角主值的确定

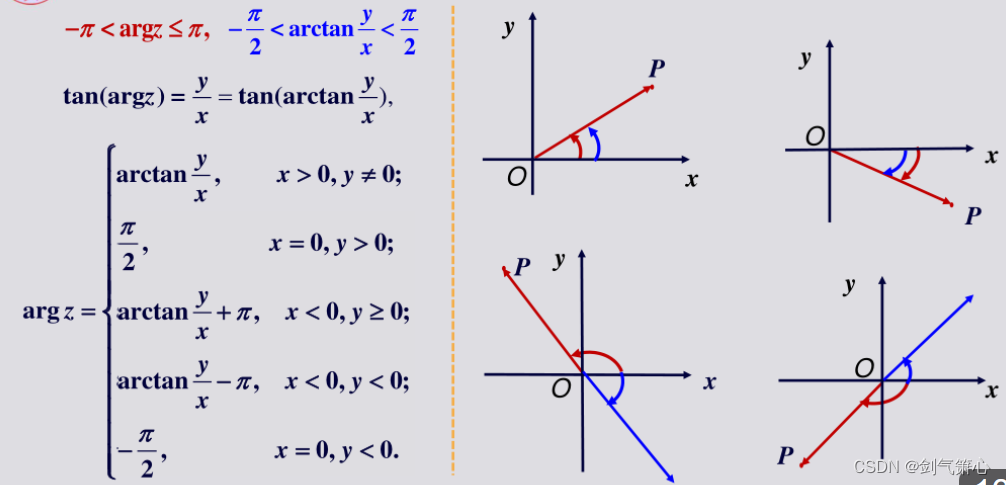
*一四象限两相等，二加π，三减π；

(3)辐角与模长的性质

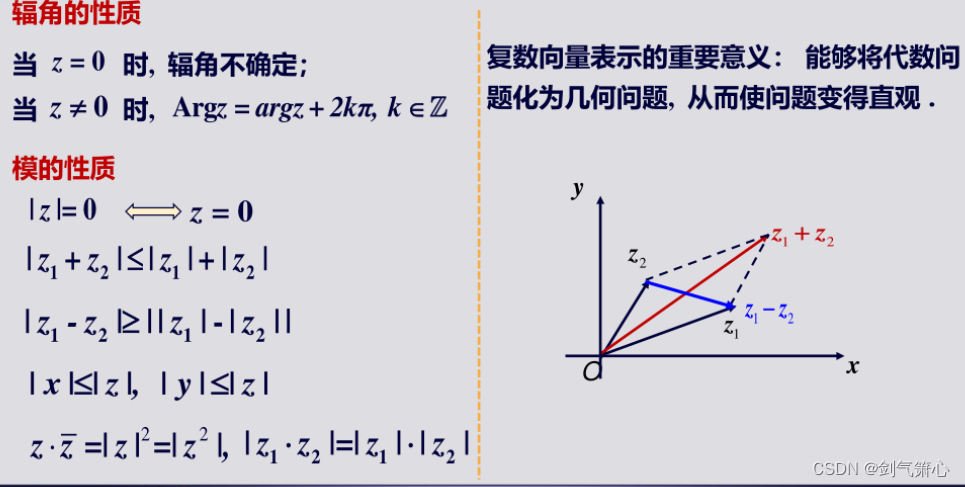
*模长的性质中2.3两条是三角不等式（两边之和大于第三边，两边之差小于第三边），需要懂这个证明过程（显然这里使用了之前的共轭复数的性质，可以把第一步两复数的和看做一个复数。复数模长的平方等于）：

*模长的性质在证明题中常考，必须记住！

4.三角表示法

5.指数表示法

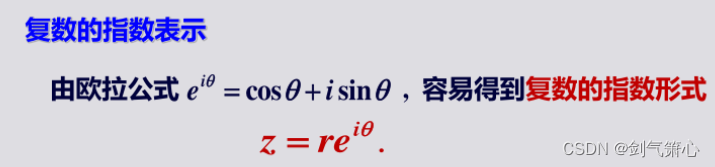
*结合复数的三角形式推导出来的

6.复球面表示法

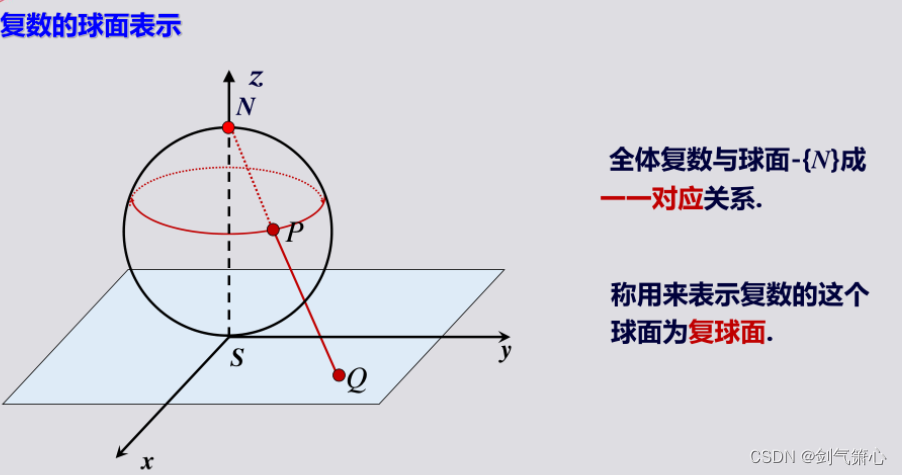
*扩充复平面我们不做介绍；

*如不声明，一般使用的都是有限复平面。

(四)复数的乘幂与方根

*前边的欧拉公式和这里的棣莫弗公式都是第一节非常重要的知识点！请务必记住。

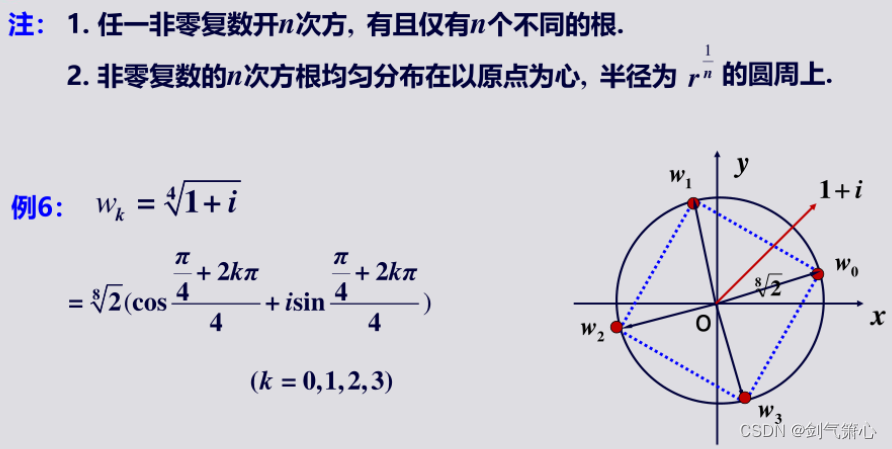
(五)复数在几何上的应用

***这些基本的都要记住，后边积分有一类小题型可以用到！

文章来源:https://blog.csdn.net/2202_76010026/article/details/135725730
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！