Transformer梳理与总结
?其实transformer的成功也是源于对注意力机制的应用,其本质上还是可以归因于注意力机制,首先我们先来了解一下什么是注意力机制。在注意力机制的背景下,自主性提示被称为查询(query),给定任何查询,注意力机制通过注意力汇聚(attention pooling) 将选择引导至感官输入(sensory inputs,例如中间特征表示)

?通过给定的查询,与键值进行计算,得到不同的注意力权重,这里注意力汇聚操作是得到由查询和键值计算出的权重先进行加权 然后再求和 ,得到加权平均值,根据加权方式的不同又可以分为非参注意力汇聚和带参注意力汇聚
非参数注意力汇聚(Nadaraya-Watson kernel regression)
?x是查询,
(
x
i
,
y
i
)
(x_i,y_i)
(xi?,yi?)是键值对,将查询x和键值对建模为注意力权重(attention weight),那么注意力汇聚操作就是对
y
i
y_i
yi?的加权平均
α
(
x
,
x
i
)
=
=
>
f
(
x
)
=
∑
i
=
1
n
K
(
x
?
x
i
)
∑
j
=
1
n
K
(
x
?
x
j
)
y
i
,
\alpha(x,x_i) ==>f(x)=\sum_{i=1}^n\frac{K(x-x_i)}{\sum_{j=1}^nK(x-x_j)}y_i,
α(x,xi?)==>f(x)=i=1∑n?∑j=1n?K(x?xj?)K(x?xi?)?yi?,
f
(
x
)
=
∑
i
=
1
n
α
(
x
,
x
i
)
y
i
,
f(x)=\sum_{i=1}^n\alpha(x,x_i)y_i,
f(x)=i=1∑n?α(x,xi?)yi?,
?为了便于理解,可以借鉴这个高斯核的例子

带参数注意力汇聚
?从上述高斯核的例子出发,在计算查询x和键值x_i之间的距离时,加入权重参数
f
(
x
)
=
∑
i
=
1
n
α
(
x
,
x
i
)
y
i
=
∑
i
=
1
n
exp
?
(
?
1
2
(
(
x
?
x
i
)
w
)
2
)
∑
j
=
1
n
exp
?
(
?
1
2
(
(
x
?
x
j
)
w
)
2
)
y
i
=
∑
i
=
1
n
softmax
(
?
1
2
(
(
x
?
x
i
)
w
)
2
)
y
i
.
\begin{aligned} f(x)& =\sum_{i=1}^n\alpha(x,x_i)y_i \\ &=\sum_{i=1}^n\frac{\exp\left(-\frac12((x-x_i)w)^2\right)}{\sum_{j=1}^n\exp\left(-\frac12((x-x_j)w)^2\right)}y_i \\ &=\sum_{i=1}^n\text{softmax}\left(-\frac12((x-x_i)w)^2\right)y_i. \end{aligned}
f(x)?=i=1∑n?α(x,xi?)yi?=i=1∑n?∑j=1n?exp(?21?((x?xj?)w)2)exp(?21?((x?xi?)w)2)?yi?=i=1∑n?softmax(?21?((x?xi?)w)2)yi?.?
注意力评分函数
? 其实刚才讲的是两种注意力汇聚的方式,也就是说算一下查询值和键值之间的相似性,然后加权到y上。这里讲注意力汇聚的计算又进行了细化,通过softmax得到概率值之后再加权到值上,最终得到输出。注意力评分函数也就是研究怎么评判键值和查询值之间的相关性

加性注意力(additive attention)
?当查询和键是不同长度的矢量时(masked-softmax),可以使用加性注意力作为评分函数
a
(
q
,
k
)
=
w
v
?
t
a
n
h
(
W
q
q
+
W
k
k
)
∈
R
,
a(\mathbf{q},\mathbf{k})=\mathbf{w}_v^\top\mathrm{tanh}(\mathbf{W}_q\mathbf{q}+\mathbf{W}_k\mathbf{k})\in\mathbb{R},
a(q,k)=wv??tanh(Wq?q+Wk?k)∈R,
?将查询和键连结起来后输入到一个多层感知机(MLP)中, 感知机包含一个隐藏层,其隐藏单元数是一个超参数h,通过使用tanh作为激活函数,并且禁用偏置项
缩放点积注意力(scaled dot-product attention)
?点积操作要求查询和键具有相同的长度,假设查询和键的所有元素都是独立的随机变量, 并且都满足零均值和单位方差,其评价函数为
a
(
q
,
k
)
=
q
?
k
/
d
.
a(\mathbf{q},\mathbf{k})=\mathbf{q}^\top\mathbf{k}/\sqrt d.
a(q,k)=q?k/d?.
多头注意力
?多头也就是说,独立学习多组注意力结果,然后再汇聚起来,相当于说,增加多样性,从多个角度看问题

h
i
=
f
(
W
i
(
q
)
q
,
W
i
(
k
)
k
,
W
i
(
v
)
v
)
∈
R
p
v
,
\mathbf{h}_i=f(\mathbf{W}_i^{(q)}\mathbf{q},\mathbf{W}_i^{(k)}\mathbf{k},\mathbf{W}_i^{(v)}\mathbf{v})\in\mathbb{R}^{p_v},
hi?=f(Wi(q)?q,Wi(k)?k,Wi(v)?v)∈Rpv?,
W
o
[
h
1
?
h
h
]
∈
R
p
o
.
\mathbf{W}_o\begin{bmatrix}\mathbf{h}_1\\\vdots\\\mathbf{h}_h\end{bmatrix}\in\mathbb{R}^{p_o}.
Wo?
?h1??hh??
?∈Rpo?.
?如上式所示,给定一组qkv 就可以得到一个注意力结果h,且每个qkv都由权重w来决定,最后在汇聚时,也要乘以权重w,这些权重都是可学习参数
自注意力和位置编码
?我觉得这事其实很简单,自注意力也就是说,q k v 均有x乘以权重得到,然后使用上述的注意力汇聚机制进行计算

Transformer
?Transformer其实就是在完全基于注意力机制的基础上,构建了一个编码器-解码器架构

?每层都使用了残差连接,这里使用的layer normalization(关于为什么不适用batch normalizetion(13分钟)),之后添加了一个FFN层,等价于两层核窗口为1的一维卷积层。之后编码器的输出作为解码器种多头注意力的V(值)和K(键),而q呢,则是通过mask-attention逐个输入进来,mask机制让其只考虑要预测位置之前所有位置的特征值
VIT
?VIT证明了模型越大效果越好,成为了transformer在CV领域应用的里程碑著作,当拥有足够多的数据进行预训练的时候,ViT的表现就会超过CNN
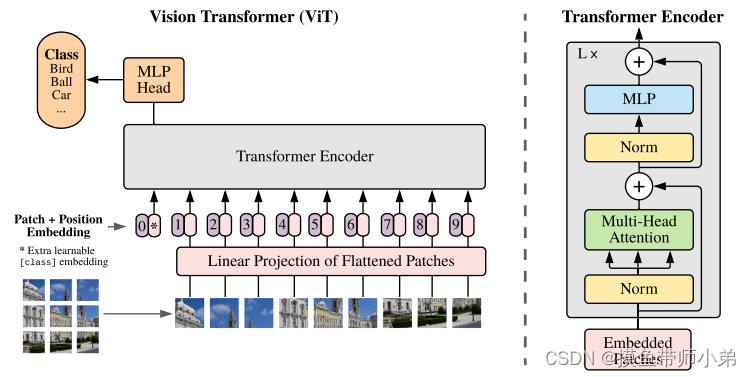
?从上图可以看出,这个网络只有编码模块,并没有解码模块,通过多层编码之后,接一个MLP用于分类任务,作者只在论文中,证明了VIT可以在分类任务上,有很好的效果,对于分割、检测等其他任务,作者没有验证。
DETR
?将transformers运用到了object detection领域,并且取代了非极大值抑制、anchor generation

?作者首先通过CNN作为backbone 进行image embeding,然后再通过一个transformer 的encoder-decoder结构,之后通过FFN层预测目标位置,作者提出一张图中预测100个框,由于不做nms,作者采用的是匈牙利算法,进行最优匹配,每个true anchor都从这个100个预测结果中匹配到一个最优的预测,然后再进行后续损失的计算
MoCo
?这篇文章是基于对比学习机制,首先介绍一下对比学习

?
x
i
x_i
xi?属于正样本,其余的都属于负样本,上面画的
x
i
x_i
xi?通过
T
1
T_1
T1?进行特征提取得到的是正样本,称为anchor,这里也作为q,通过
T
2
T_2
T2?进行特征提取的作为
x
i
x_i
xi?的一个正样本,因为正样本和负样本都是相对于anchor来说的,因此其余的负样本也应该经过
T
2
T_2
T2?进行特征提取,作为k
?字典里面的K值都应该由相同或者相似的编码器得到,这里作者就提出了动量对比学习的概念。同时为了避免字典过大,作者讲数据结构中队列的思想应用进来,新的batch数据进来时,之前的数据就丢出去
?作者选用个体判别的方法作为代理任务去训练整个网络,然后再将其迁移到分类任务中
参考资料
- 动手深度学习 https://zh-v2.d2l.ai/chapter_attention-mechanisms/attention-cues.html
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!