Java实现LeetCode173.二叉搜索树迭代器
发布时间:2024年01月09日
题目描述
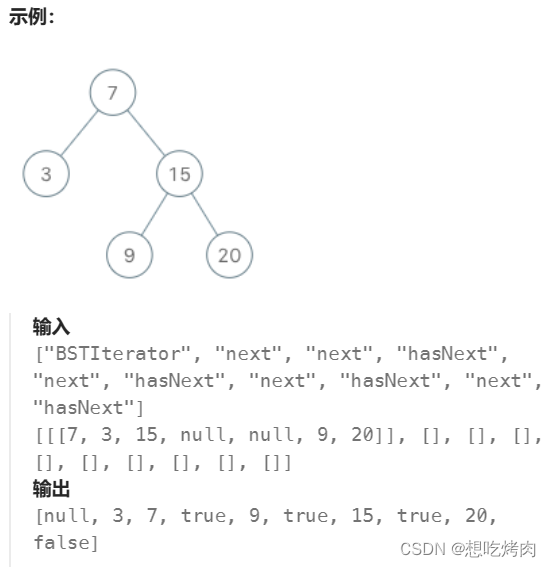
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字,则返回 true ;否则返回 false 。
int next() 将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
思路
题目中的next()函数实际上要求我们按照中序遍历二叉树。
方法一:一个直接的思路是在BSTIterator(TreeNode root)初始化函数中,就对二叉搜索树进行一次中序遍历,保留在全局变量list中,每次调用next()或hasNext()转为遍历list。也是官解中的 “扁平化”。
方法二:不难想到通过递归简单地实现二叉树的中序遍历。但是一旦开始递归,就要递归完所有节点。但现在希望 每调用一次next(),就只访问到对应节点 ,而递归本质上是通过栈实现的,所以可以应用栈实现。
所以,方法二本质上是通过迭代实现了二叉树中序遍历。
代码
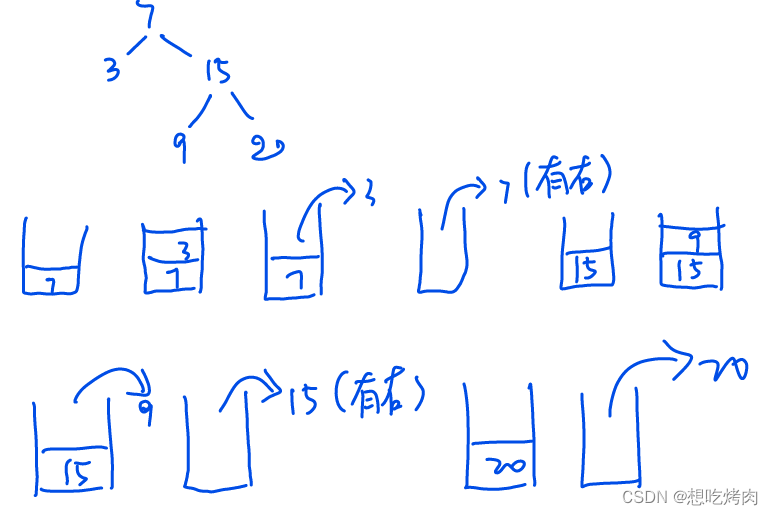
迭代思路:若节点有左子节点,则不断入栈;出栈的节点若有右子节点,则入栈。
class BSTIterator {
Deque<TreeNode> dq = new LinkedList();
public BSTIterator(TreeNode root) {
dq.add( root );
while( root != null ){
if( root.left != null ){
dq.push( root.left );
}
root = root.left;
}
}
public int next() {
TreeNode tmp = dq.pop();
if( tmp.right!=null ){
TreeNode root = tmp.right;
dq.push( root );
while( root != null ){
if( root.left != null ){
dq.push( root.left );
}
root = root.left;
}
}
return tmp.val;
}
public boolean hasNext() {
return !dq.isEmpty();
}
}
思考
二叉树的遍历真是常写常新
文章来源:https://blog.csdn.net/weixin_43273560/article/details/135448176
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章