算法问题：最优二叉搜索树

发布时间：2023年12月25日

给定一个序列K=<{k_{1},k_{2},...,k_{n}}> 有n个有序且各不相同的键(k_{1}<k_{2}<...<k_{n})， 集合
P=<{p_{1},p_{2},...,p_{n}}>表示在K中成功的搜索的概率;D=<{d_{0},d_{1},d_{2},...,d_{n}}> 为n+1 个不同的哑键，d_{i}表示所有在k_{i}和k_{i+1}之间的值，Q=<{q_{0},q_{1},q_{2},...,q_{n}}> 表示不成功的搜索的概率. 创建二叉搜索树， 使得其期望搜索花费最小。

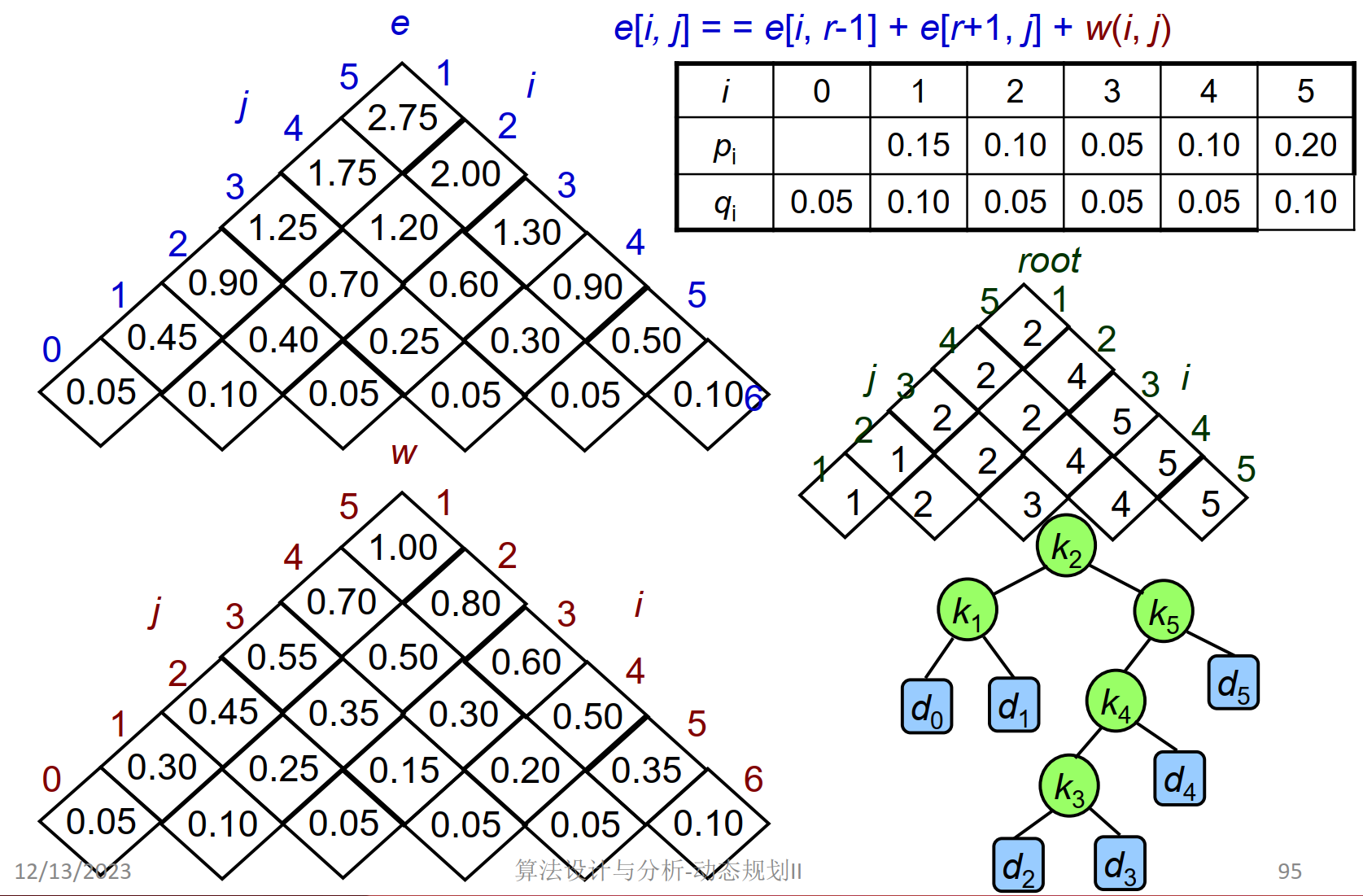
一个例子

最优子结构

如果一棵最优二叉搜索树T的子树T’含有键k_{i},...,k_{j}那么这个子树T’肯定是子问题键k_{i},...,k_{j}和哑

键d_{i-1},...,d_{j}的最优解。 (利用反证法证明)

重叠子问题解决思路: 递归

解释为什么要加w(i,r-1)与w(r+1,j)

当一颗子树成为结点的子树时，由于每个结点的深度都增加了1，这颗子树的期望搜索代价的增加值应该为所有概率之和。

e[1,3]=p_{2}+(e[1,1]+w(1,1))+(e[3,3]+w(3,3)) \\=0.2+(e[1,1]+0.3)+(e[3,3]+0.4)=0.2+0.3*2^{\normalsize{\textcircled{\scriptsize{1}}}\normalsize\enspace}+0.4*2^{\normalsize{\textcircled{\scriptsize{1}}}\normalsize\enspace }

{\textcircled{\scriptsize{1}}}\normalsize\enspace这个增加值才能体现该结点在搜索时对应的深度代价

计算最优费用(与计算矩阵李安乘法问题类似)

举例使用递归解结构

文章来源:https://blog.csdn.net/weixin_50917576/article/details/135205562
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章