数据结构与算法教程,数据结构C语言版教程!(第二部分、线性表详解:数据结构线性表10分钟入门)一
第二部分、线性表详解:数据结构线性表10分钟入门

线性表,数据结构中最简单的一种存储结构,专门用于存储逻辑关系为"一对一"的数据。
线性表,基于数据在实际物理空间中的存储状态,又可细分为顺序表(顺序存储结构)和链表(链式存储结构)。
本章还会讲解顺序表和链表的结合体——静态链表,不仅如此,还会涉及循环链表、双向链表、双向循环链表等链式存储结构。
一、什么是线性表(线性存储结构)
通过前面的学习我们知道,具有“一对一”逻辑关系的数据,最佳的存储方式是使用线性表。那么,什么是线性表呢?
线性表,全名为线性存储结构。使用线性表存储数据的方式可以这样理解,即“把所有数据用一根线儿串起来,再存储到物理空间中”。
![]()
图 1 "一对一"逻辑关系的数据
如图 1 所示,这是一组具有“一对一”关系的数据,我们接下来采用线性表将其储存到物理空间中。
首先,用“一根线儿”把它们按照顺序“串”起来,如图 2 所示:

图 2 数据的"线性"结构
图 2 中,左侧是“串”起来的数据,右侧是空闲的物理空间。把这“一串儿”数据放置到物理空间,我们可以选择以下两种方式,如图 3 所示。
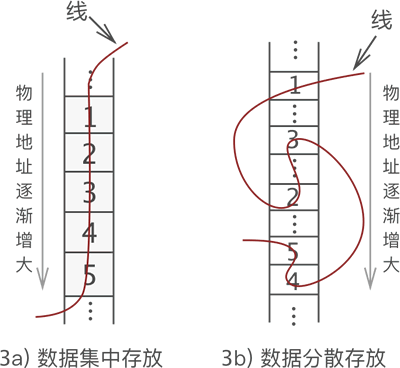
图 3 两种线性存储结构
图 3a) 是多数人想到的存储方式,而图 3b) 却少有人想到。我们知道,数据存储的成功与否,取决于是否能将数据完整地复原成它本来的样子。如果把图 3a) 和图 3b) 线的一头扯起,你会发现数据的位置依旧没有发生改变(和图 1 一样)。因此可以认定,这两种存储方式都是正确的。
将具有“一对一”关系的数据“线性”地存储到物理空间中,这种存储结构就称为线性存储结构(简称线性表)。
使用线性表存储的数据,如同向数组中存储数据那样,要求数据类型必须一致,也就是说,线性表存储的数据,要么全部都是整形,要么全部都是字符串。一半是整形,另一半是字符串的一组数据无法使用线性表存储。
1、顺序存储结构和链式存储结构
图 3 中我们可以看出,线性表存储数据可细分为以下 2 种:
- 如图 3a) 所示,将数据依次存储在连续的整块物理空间中,这种存储结构称为顺序存储结构((简称顺序表);
- 如图 3b) 所示,数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系,这种存储结构称为链式存储结构(简称链表);
也就是说,线性表存储结构可细分为顺序存储结构和链式存储结构。
2、前驱和后继
数据结构中,一组数据中的每个个体被称为“数据元素”(简称“元素”)。例如,图 1 显示的这组数据,其中 1、2、3、4 和 5 都是这组数据中的一个元素。
另外,对于具有“一对一”逻辑关系的数据,我们一直在用“某一元素的左侧(前边)或右侧(后边)”这样不专业的词,其实线性表中有更准确的术语:
- 某一元素的左侧相邻元素称为“直接前驱”,位于此元素左侧的所有元素都统称为“前驱元素”;
- 某一元素的右侧相邻元素称为“直接后继”,位于此元素右侧的所有元素都统称为“后继元素”;
以图 1 数据中的元素 3 来说,它的直接前驱是 2 ,此元素的前驱元素有 2 个,分别是 1 和 2;同理,此元素的直接后继是 4 ,后继元素也有 2 个,分别是 4 和 5。如图 4 所示:
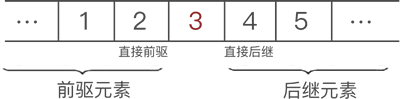
图 4 前驱和后继
?二、顺序表(顺序存储结构)及初始化详解
顺序表,全名顺序存储结构,是线性表的一种。通过《一、什么是线性表》一节的学习我们知道,线性表用于存储逻辑关系为“一对一”的数据,顺序表自然也不例外。
不仅如此,顺序表对数据的物理存储结构也有要求。顺序表存储数据时,会提前申请一整块足够大小的物理空间,然后将数据依次存储起来,存储时做到数据元素之间不留一丝缝隙。
例如,使用顺序表存储集合?{1,2,3,4,5},数据最终的存储状态如图 1 所示:

图 1 顺序存储结构示意图
由此我们可以得出,将“具有 '一对一' 逻辑关系的数据按照次序连续存储到一整块物理空间上”的存储结构就是顺序存储结构。
通过观察图 1 中数据的存储状态,我们可以发现,顺序表存储数据同数组非常接近。其实,顺序表存储数据使用的就是数组。
1、顺序表的初始化
使用顺序表存储数据之前,除了要申请足够大小的物理空间之外,为了方便后期使用表中的数据,顺序表还需要实时记录以下 2 项数据:
- 顺序表申请的存储容量;
- 顺序表的长度,也就是表中存储数据元素的个数;
提示:正常状态下,顺序表申请的存储容量要大于顺序表的长度。
因此,我们需要自定义顺序表,C 语言实现代码如下:
typedef struct Table{
???????? int * head;//声明了一个名为head的长度不确定的数组,也叫“动态数组”
???????? int length;//记录当前顺序表的长度
????????int size;//记录顺序表分配的存储容量
}table;
注意,head 是我们声明的一个未初始化的动态数组,不要只把它看做是普通的指针。
接下来开始学习顺序表的初始化,也就是初步建立一个顺序表。建立顺序表需要做如下工作:
- 给 head 动态数据申请足够大小的物理空间;
- 给 size 和 length 赋初值;
因此,C 语言实现代码如下:
#define Size 5 //对Size进行宏定义,表示顺序表申请空间的大小
table initTable(){
????????table t; t.head=(int*)malloc(Size*sizeof(int));//构造一个空的顺序表,动态申请存储空间
????????if (!t.head) //如果申请失败,作出提示并直接退出程序
????????{
????????????????printf("初始化失败");
????????????????exit(0);
????????}
????????t.length=0;//空表的长度初始化为0
????????t.size=Size;//空表的初始存储空间为Size
????????return t;
}
我们看到,整个顺序表初始化的过程被封装到了一个函数中,此函数返回值是一个已经初始化完成的顺序表。这样做的好处是增加了代码的可用性,也更加美观。与此同时,顺序表初始化过程中,要注意对物理空间的申请进行判断,对申请失败的情况进行处理,这里只进行了“输出提示信息和强制退出”的操作,可以根据你自己的需要对代码中的 if 语句进行改进。
通过在主函数中调用 initTable 语句,就可以成功创建一个空的顺序表,与此同时我们还可以试着向顺序表中添加一些元素,C 语言实现代码如下:
#include <stdio.h>
#include <stdlib.h>
#define Size 5
typedef struct Table{
????????int * head;
????????int length;
????????int size;
}table;
table initTable(){
????????table t;
????????t.head=(int*)malloc(Size*sizeof(int));
????????if (!t.head)
????????{
????????????????printf("初始化失败");
????????????????exit(0);
????????}
????????t.length=0;
????????t.size=Size;
????????return t;
}
//输出顺序表中元素的函数
void displayTable(table t){
????????for (int i=0;i<t.length;i++) {
????????????????printf("%d ",t.head[i]);
????????}
????????printf("\n");
}
int main(){
????????table t=initTable();
????????//向顺序表中添加元素
????????for (int i=1; i<=Size; i++) {
????????????????t.head[i-1]=i;
????????????????t.length++;
????????}
????????printf("顺序表中存储的元素分别是:\n");
????????displayTable(t);
????????return 0;
}
程序运行结果如下:
顺序表中存储的元素分别是:
1 2 3 4 5
可以看到,顺序表初始化成功。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【毕业设计】springboot+vue演唱会门票购票系统
- Repo代码仓库搭建
- Armv8-M的TrustZone技术之SAU寄存器总结
- java 企业工程管理系统软件源码+Spring Cloud + Spring Boot +二次开发+ 可定制化
- 0.2费率微信支付真的吗
- 在windows系统和ubuntu系统中划分数据集,图片格式为jpg只需修改路径,如果图片是png格式可以把代码中的.jpg修改成.png形式就可以运行了。
- Linux tftp命令教程:文件传输利器(附案例详解和注意事项)
- C++实现布隆过滤器
- Python的基础练习题之学生管理系统
- [mysql 基于C++实现数据库连接池 连接池的使用] 持续更新中