Pure Mathematics 3-(磨课课件)-反三角函数求导（更新中）

6.6 Differentiating trigonometric functions（反三角函数求导）
Edexcel Pure Mathematics 3(2018版本教材)
/--------------------------------------------------------------------------------------------------------------------
Prior Knowledge（预备知识温习）
①$(sinx{)}^{\prime }=cosx+C$
②$(cosx{)}^{\prime }=?sinx+C$
③$(\frac{u}{v}{)}^{\prime }=\frac{u^{\prime }v?v^{\prime }u}{v^2}$
④三角形六边形法则-对角线上 两个函数互为倒数

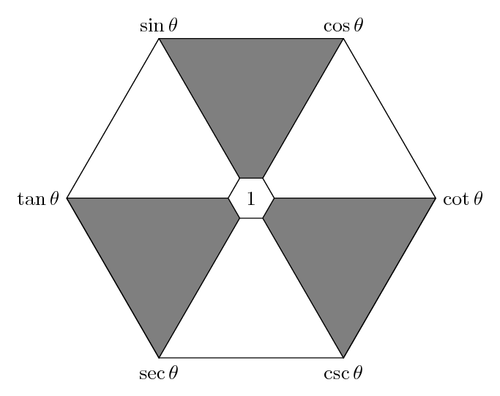
对角线上 两个函数互为倒数

根据上述知识，我们下面看一道 习题
Example 14
If $y=k?tanx$，find$\frac{dy}{dx}$

Solution:
$\begin{array}{l}y=k\tan x=k\frac{\sin x}{\cos x}\\ \text{?Let?}u=\sin x\text{v}=\cos x\\ \begin{array}{rl}\frac{du}{dx}& =\cos x\text{?and?}\frac{dv}{dx}=?\sin x\\ \frac{dy}{dx}& =k\frac{v\frac{du}{dx}?u\frac{dv}{dx}}{v^2}\\ & =k\frac{\cos x\times \cos x?\sin x(?\sin x)}{{\cos }^{2}x}\\ & =k\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}\\ & =k\frac{1}{{\cos }^{2}x}=k{\sec }^{2}x\end{array}\end{array}$

Prior Knowledge（预备知识温习）
$(uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }$
$(tanx{)}^{\prime }=se{c}^{2}x$
Example 15

$y=x\tan 2x$
$=x\times 2{\sec }^{2}2x+\tan 2x$ $=2x{\sec }^{2}2x+\tan 2x$

$y={\tan }^{4}x=(\tan x{)}^4$
$\frac{dy}{dx}=4(\tan x{)}^3({\sec }^{2}x)$
$=4{\tan }^{3}x{\sec }^{2}x$

Prior Knowledge（预备知识温习）

$\frac{1}{cosecx}=\frac{1}{sinx}(三角形六边形法则)$
$(\frac{u}{v}{)}^{\prime }=\frac{u^{\prime }v?v^{\prime }u}{v^2}$

Example 16
$\begin{array}{rl}y& =\mathrm{cosec}x=\frac{1}{\sin x}\\ \mathrm{Let}u& =1\mathrm{and}v=\sin x\\ \frac{du}{dx}& =0\mathrm{and}\frac{dv}{dx}=\cos x\end{array}$

$\begin{array}{rl}\frac{dy}{dx}& =\frac{v\frac{du}{dx}?u\frac{dv}{dx}}{v^2}\\ & =\frac{\sin x\times 0?1\times \cos x}{{\sin }^{2}x}\\ & =?\frac{\cos x}{{\sin }^{2}x}\\ & =?\frac{1}{\sin x}\times \frac{\cos x}{\sin x}=?\mathrm{cosec}x\cot x\end{array}$