C++ AVL树(四种旋转,插入)

发布时间：2023年12月20日

C++ AVL树[四种旋转,插入]

一.AVL树的概念及性质
二.我们要实现的大致框架
- 1.AVL树的节点定义
- 2.AVL树的大致框架
三.插入
四.旋转的动图演示和代码实现
五.AVL树的验证
六.完整代码
- 1.AVLTree.h:
- 2.test.cpp

一.AVL树的概念及性质

AVL树又称高度平衡二叉搜索树,它的高度接近log[2]N(以2为底N的对数),整棵树的形状接近完全二叉树
增删查改的时间复杂度是O(log[2]N)
在这里插入图片描述
本节我们实现的是Key-Value模型的AVL树

二.我们要实现的大致框架

1.AVL树的节点定义

这里我们的AVL树节点比起普通的二叉树的节点来说多了两个成员
第一个是平衡因子,这里我们定义的平衡因子是右子树高度-左子树高度
第二个是指向父节点的指针,方便找到父亲节点从而方便旋转的实现

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K,V>& data = pair<K,V>())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}
	AVLTreeNode<K,V>* _pLeft;
	AVLTreeNode<K,V>* _pRight;
	AVLTreeNode<K,V>* _pParent;
	pair<K,V> _data;
	int _bf;   // 节点的平衡因子
};

存放的数据类型是一个pair
pair的第一个值是Key
第二个值是Value

2.AVL树的大致框架

// AVL: 二叉搜索树 + 平衡因子的限制
template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	//构造函数
	AVLTree()
		: _pRoot(nullptr)
	{}

	// 在AVL树中插入值为data的节点
	bool Insert(const pair<K,V>& data);

	// AVL树的验证
	bool IsAVLTree()
	{
		return _IsAVLTree(_pRoot);
	}

	void InOrder()
	{
		_InOrder(_pRoot);
	}

private:
	//中序遍历
	void _InOrder(Node* root);

	// 根据AVL树的概念验证pRoot是否为有效的AVL树
	bool _IsAVLTree(Node* pRoot);

	//求树的高度
	size_t _Height(Node* pRoot);

	// 右单旋
	void RotateR(Node* pParent);

	// 左单旋
	void RotateL(Node* pParent);

	// 右左双旋
	void RotateRL(Node* pParent);

	// 左右双旋
	void RotateLR(Node* pParent);

private:
	Node* _pRoot;
};

三.插入

它的插入的大体逻辑跟二叉搜索树(BST)的插入逻辑很像
只不过需要考虑平衡因子的修改以及旋转
我们先把跟二叉搜索树一样的部分写出来

1.插入逻辑跟BST相同的那一部分

// 在AVL树中插入值为data的节点
bool Insert(const pair<K,V>& data)
{
	if (_pRoot == nullptr)
	{
		_pRoot = new Node(data);
		return true;
	}
	Node* cur = _pRoot, * parent = nullptr;
	//1.找插入位置
	while (cur)
	{
		if (cur->_data > data)
		{
			parent = cur;
			cur = cur->_pLeft;
		}
		else if (cur->_data < data)
		{
			parent = cur;
			cur = cur->_pRight;
		}
		else
		{
			return false;
		}
	}
	//2.new一个新节点,开始链接
	cur=new Node(data);
	//下面就是链接节点,修改平衡因子了,这也是AVL树相比于普通的BST的插入逻辑不同的地方
	return true;
}

2.修改平衡因子

1.前置说明

首先要说明:
1.新插入的节点的平衡因子是0,是在AVL树节点的构造函数当中进行初始化的
2.在插入节点的过程中,我们一直维持平衡因子的值为-1/0/1
3.一旦平衡因子到达了2或者-2,说明此时不满足AVL树的性质,需要进行旋转来调整平衡因子,使平衡因子恢复到-1/0/1的状态

2.画图演示

下面我们来画图演示一下插入节点后对于整棵树的节点的平衡因子的影响

1.情况1(一直影响到根节点为止)

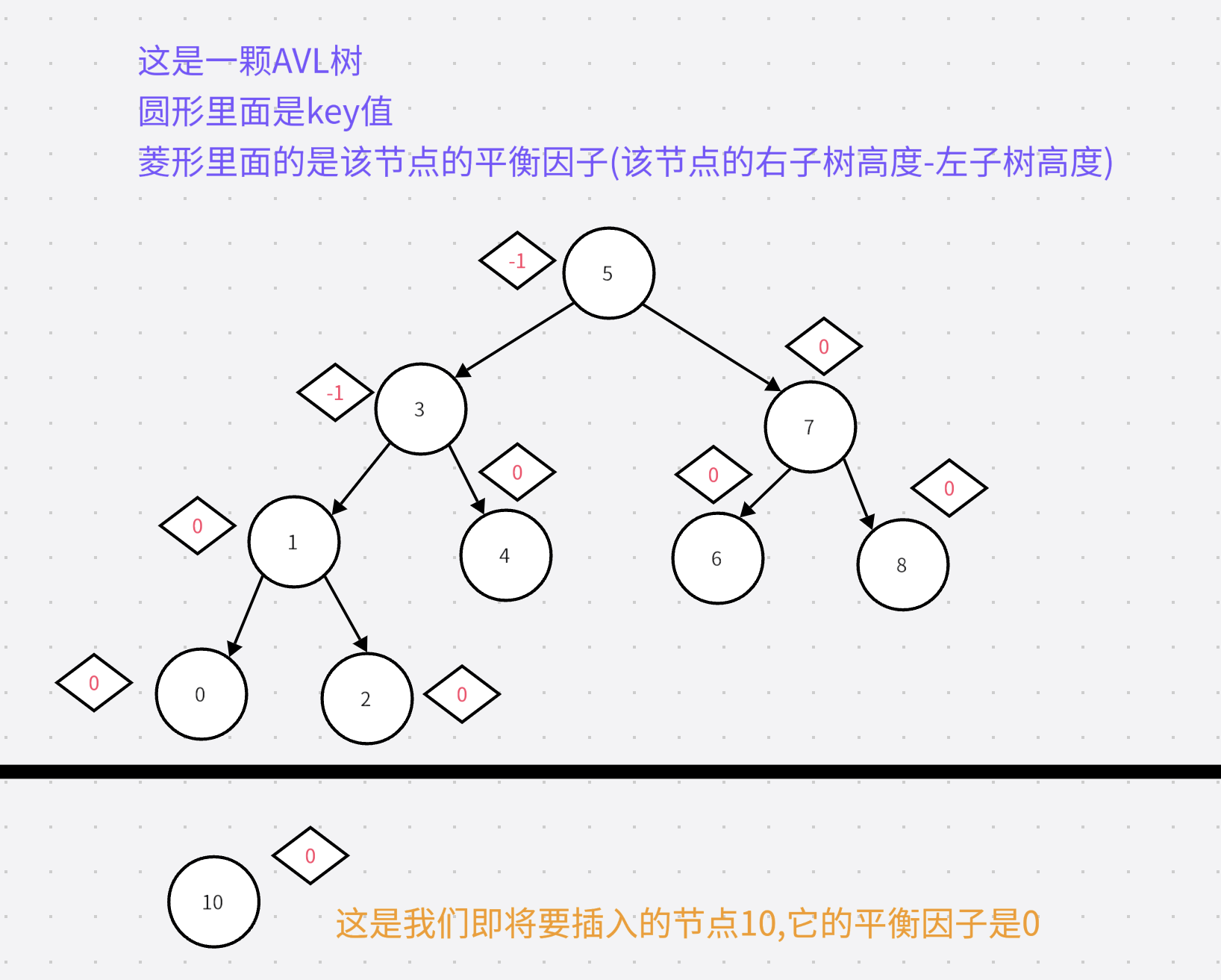
在这里插入图片描述

那不就是一直向上影响不就行了吗?
不是的,比如下面这种情况

2.情况2(在影响到根节点之前影响消失了)

为了方便演示,把节点8的值改成了9
新插入的值为8

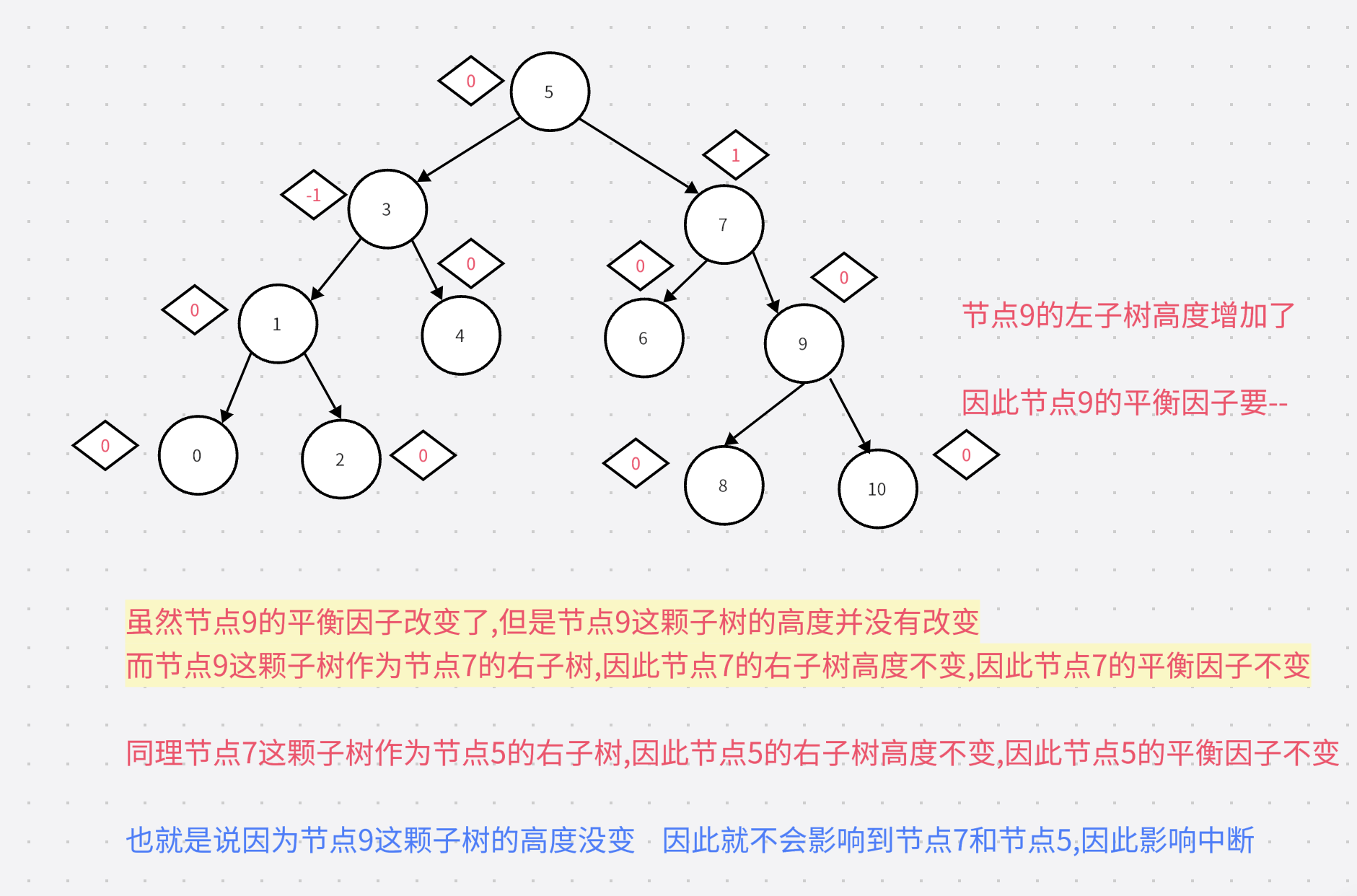
在这里插入图片描述

3.深剖情况1和2

第一种情况时:
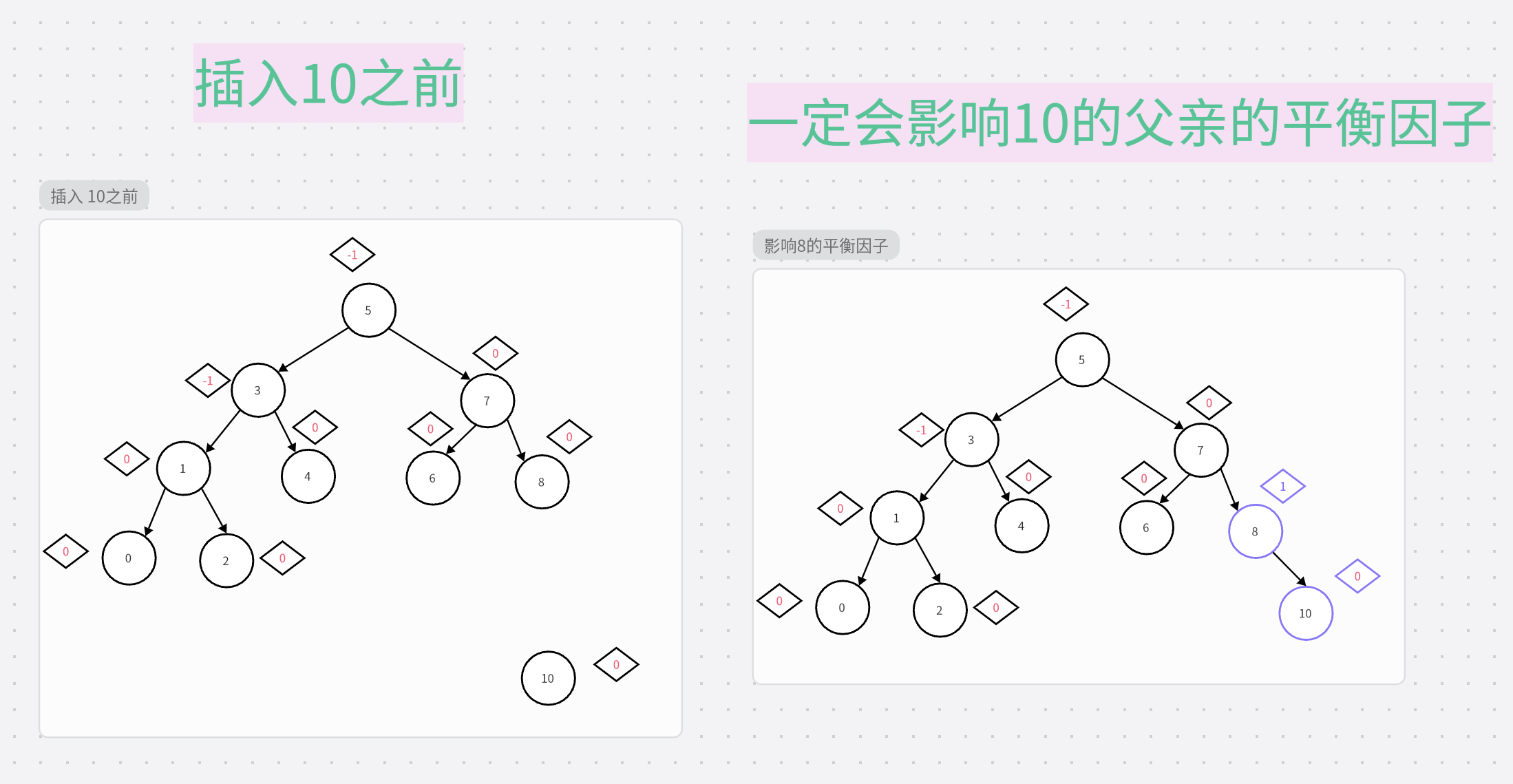
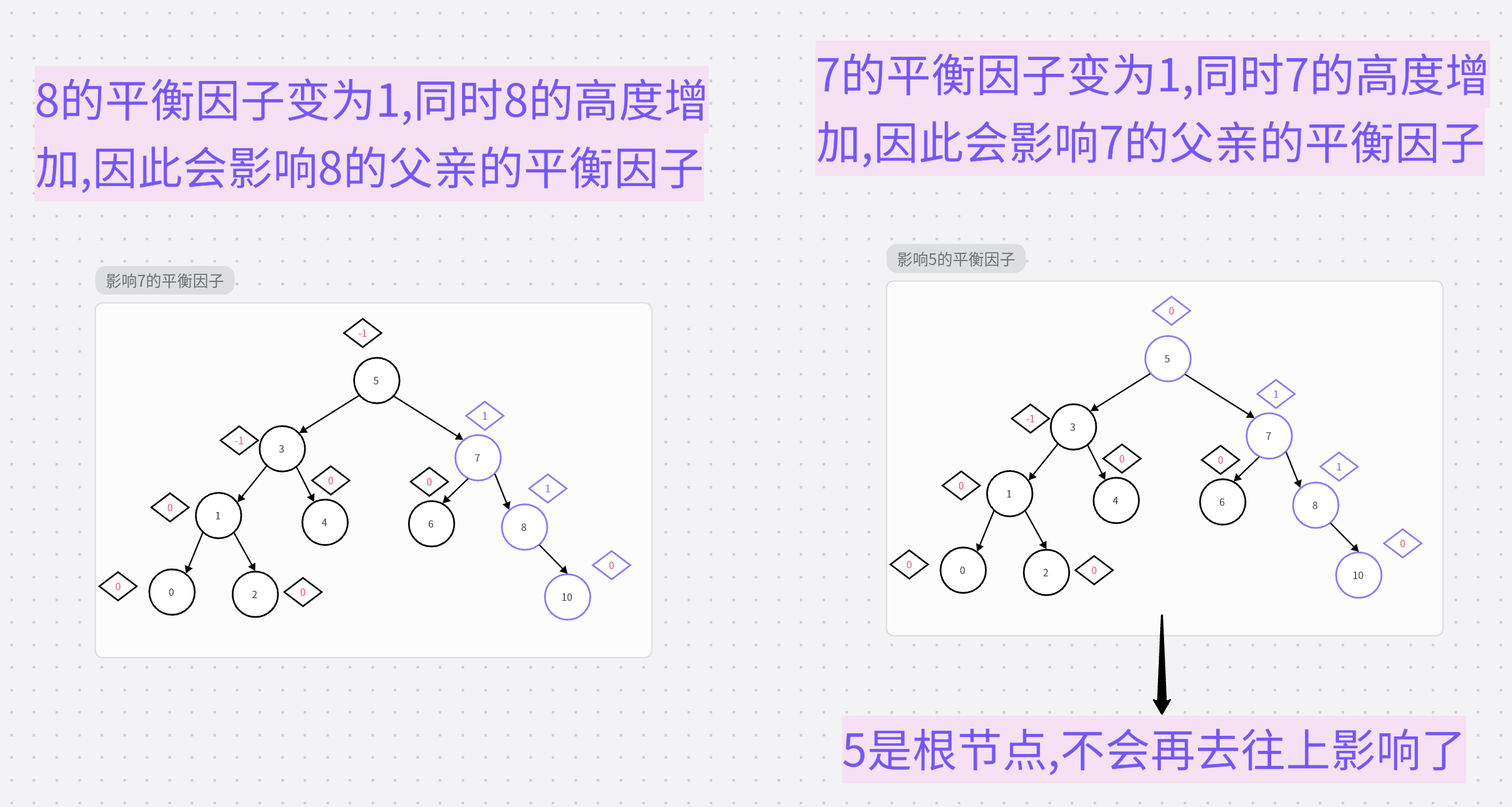
在这里插入图片描述

第二种情况时:

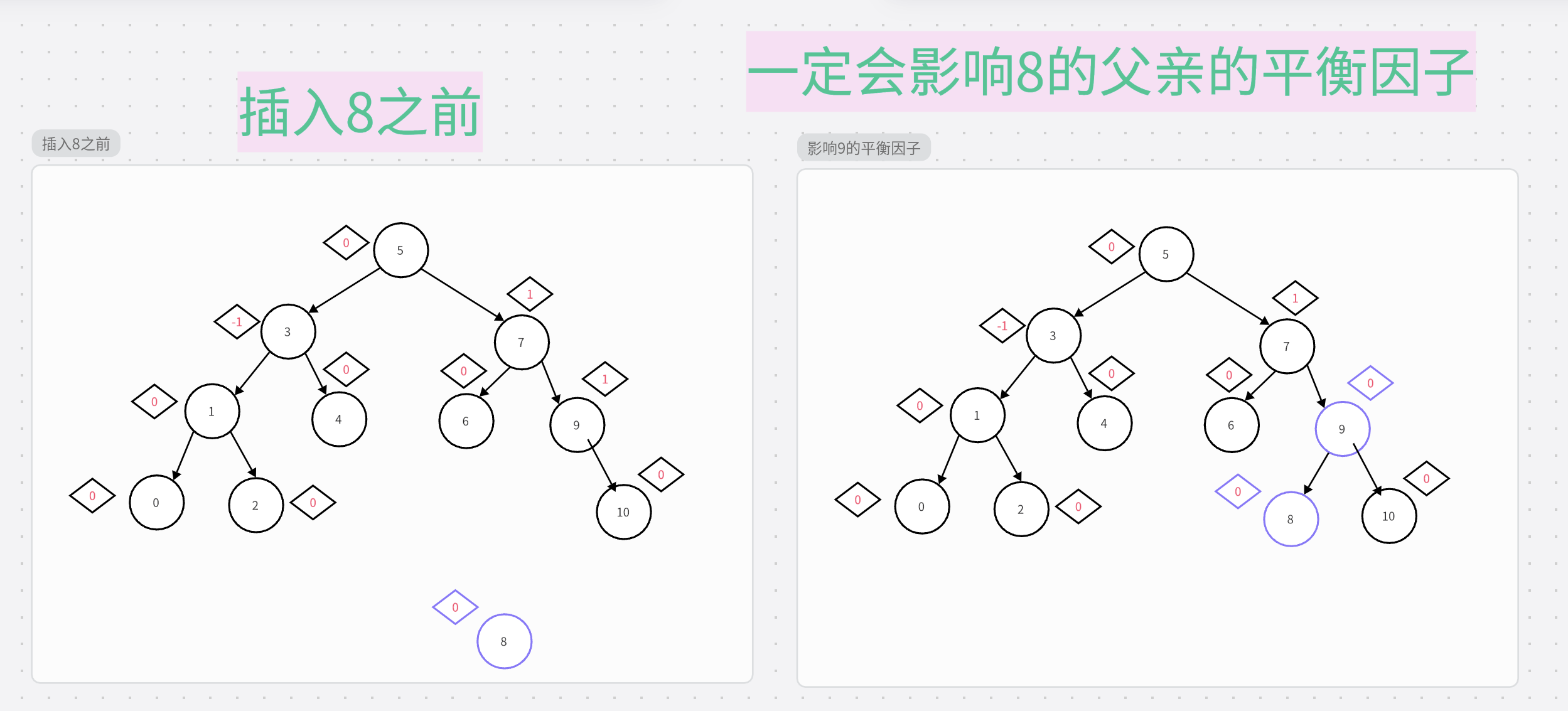
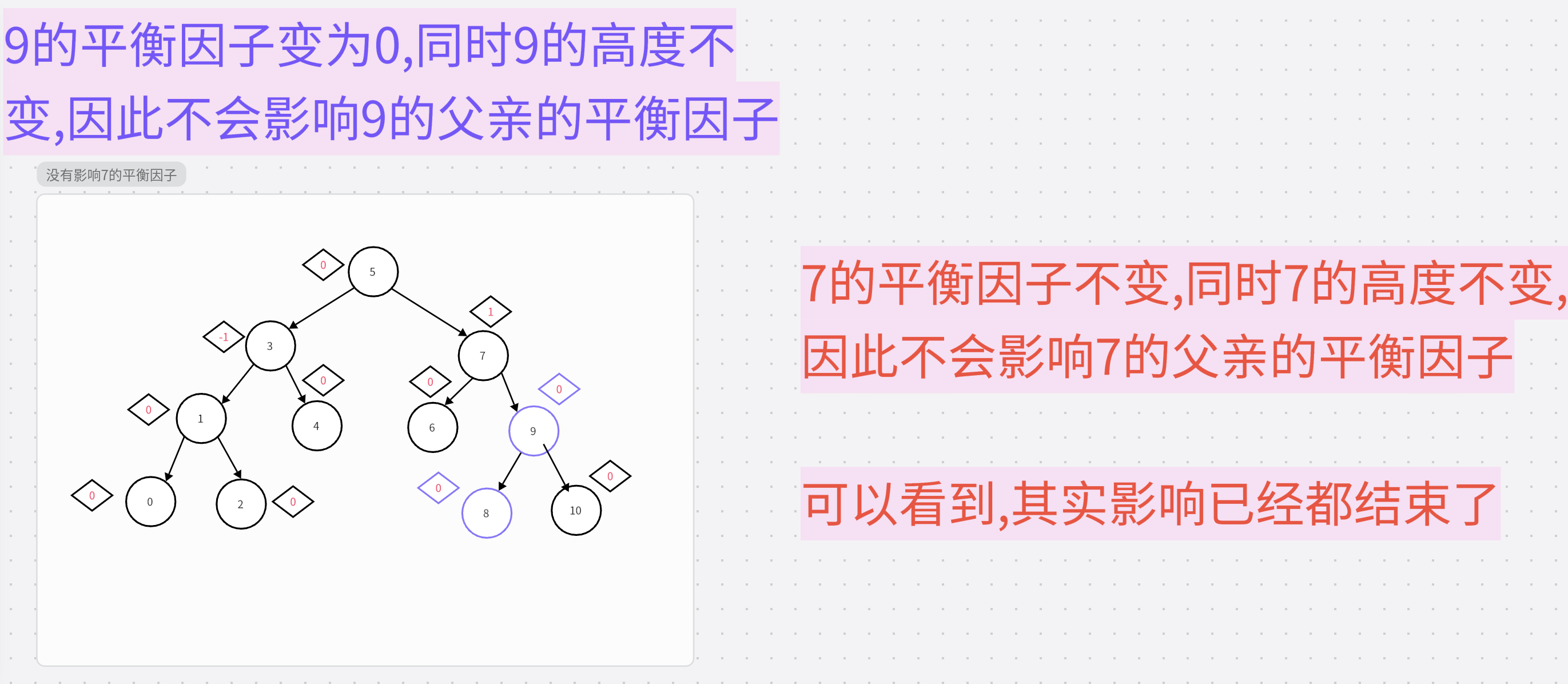
4.总结

在这里插入图片描述

3.考虑旋转

在修改平衡因子时,如果某个节点的平衡因子修改之后变为了2或者-2
说明以这个节点为根节点的子树已经不是AVL树了,需要旋转这个节点

关于如何旋转我们后面会介绍
这里先说明一下什么情况下进行哪种旋转

而旋转分为4种情况:
1.左单旋

1.左单旋的介绍

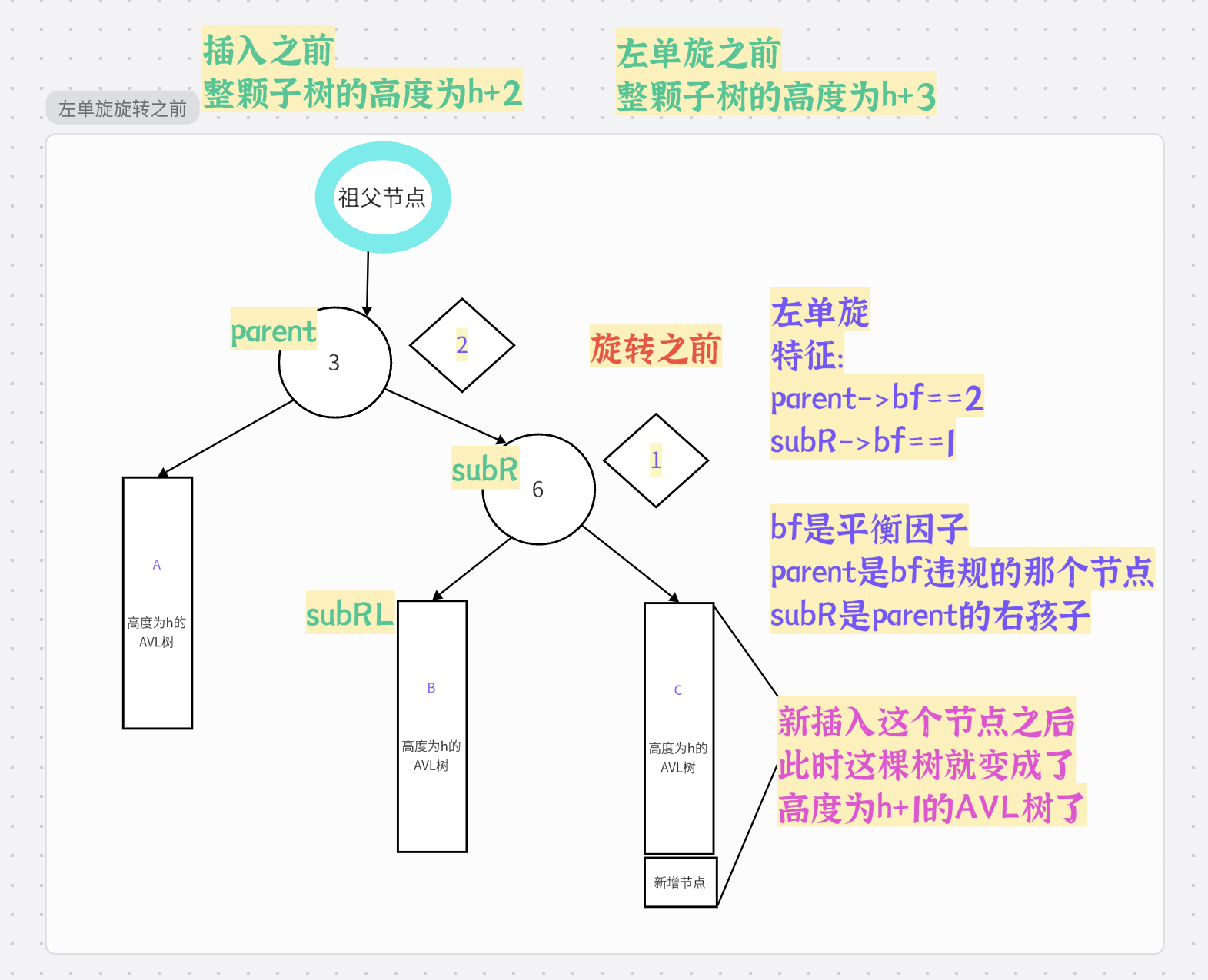
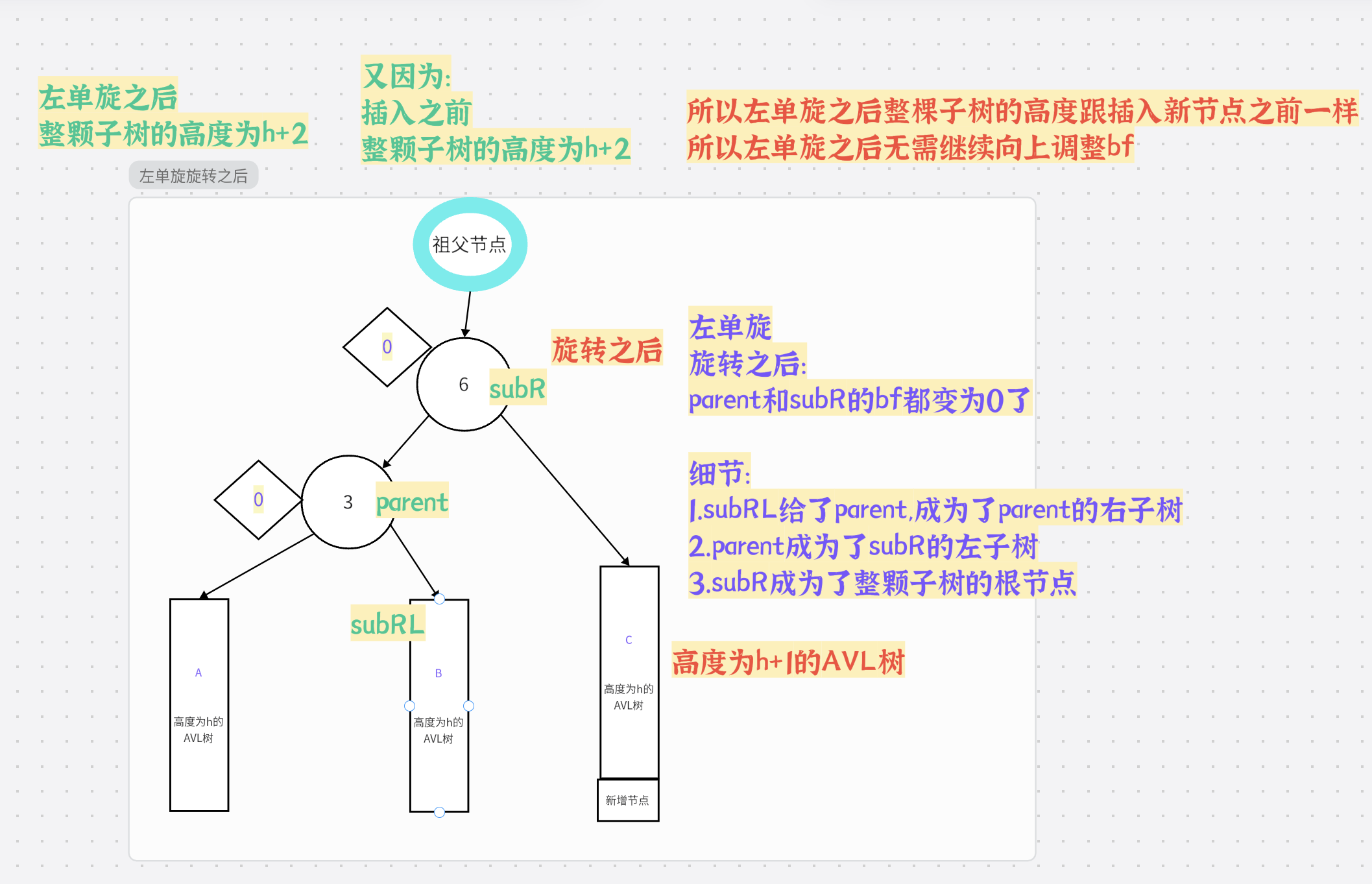
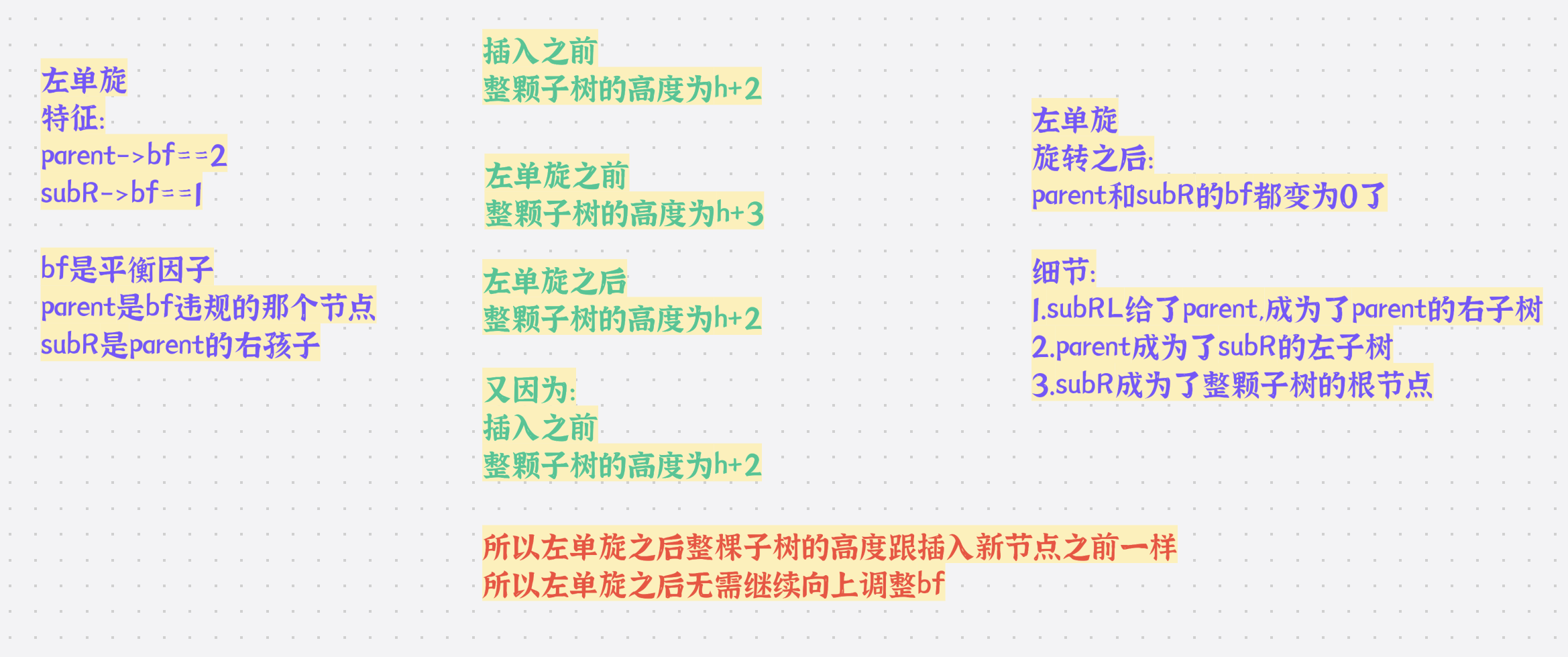
在这里插入图片描述

总结:

2.右单旋的介绍

了解了左单旋之后,右单旋也就能够很好的理解了
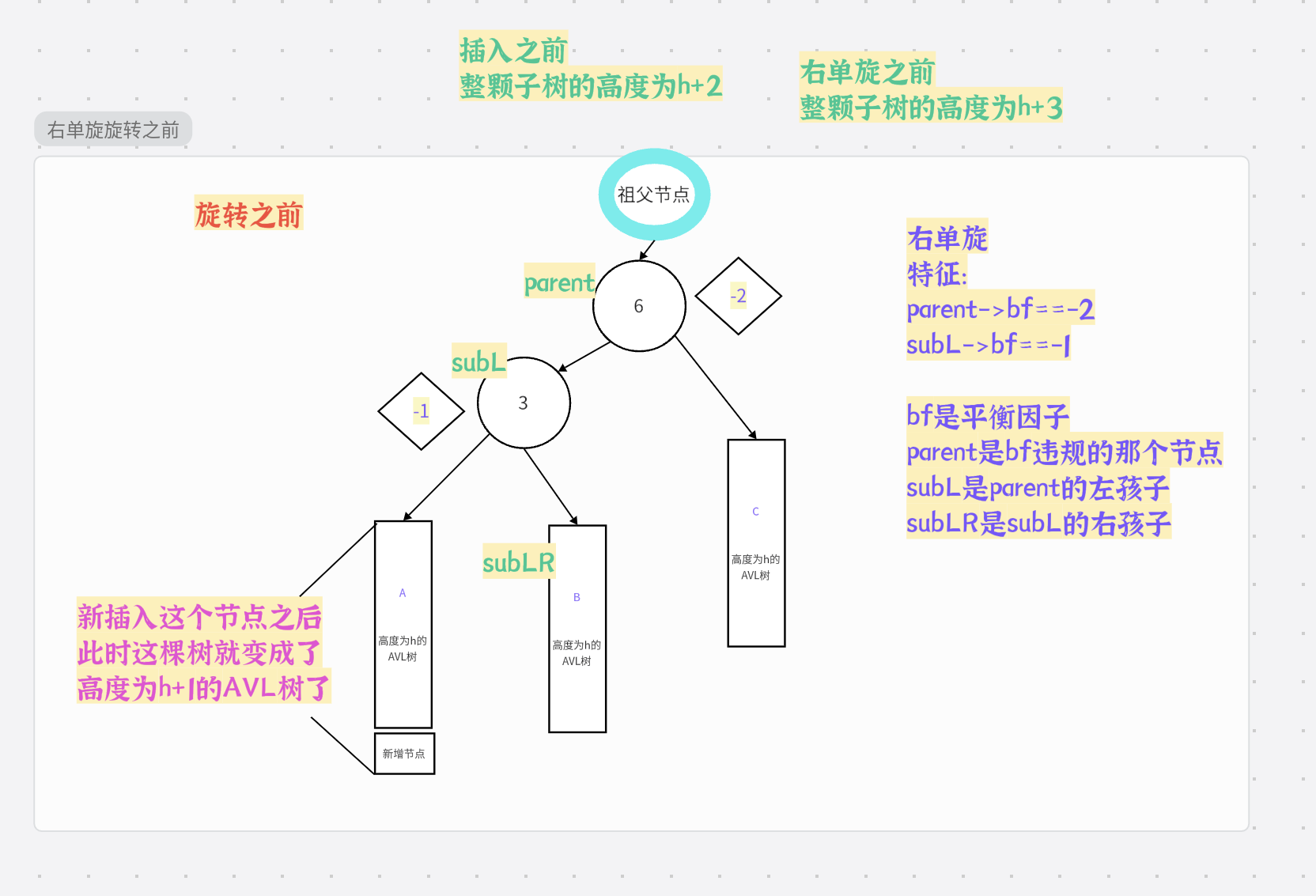
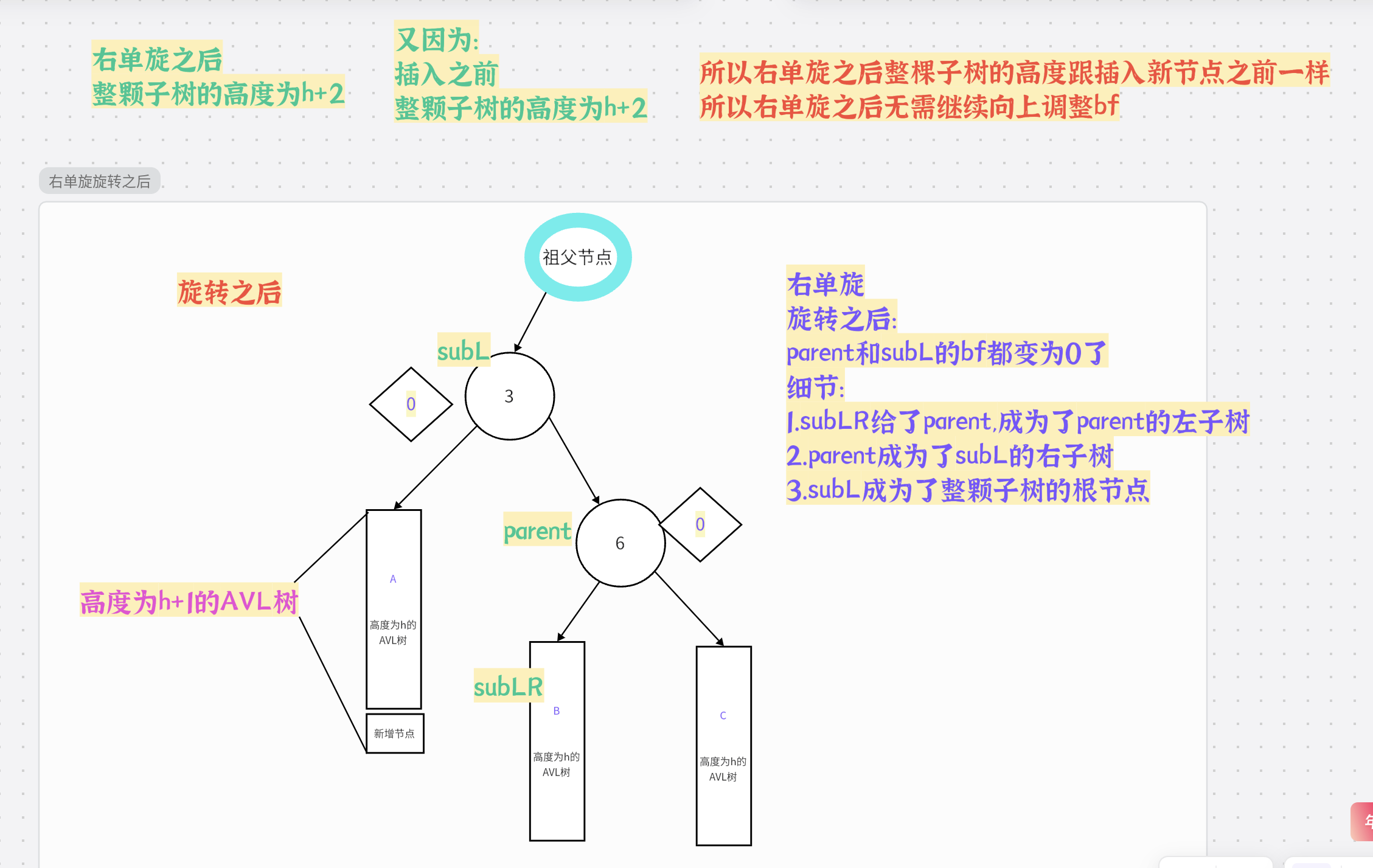
在这里插入图片描述

总结:

3.右左双旋的介绍

右左双旋的基础条件跟左单旋的基础条件很像
只不过有一点不一样,我们来看看吧
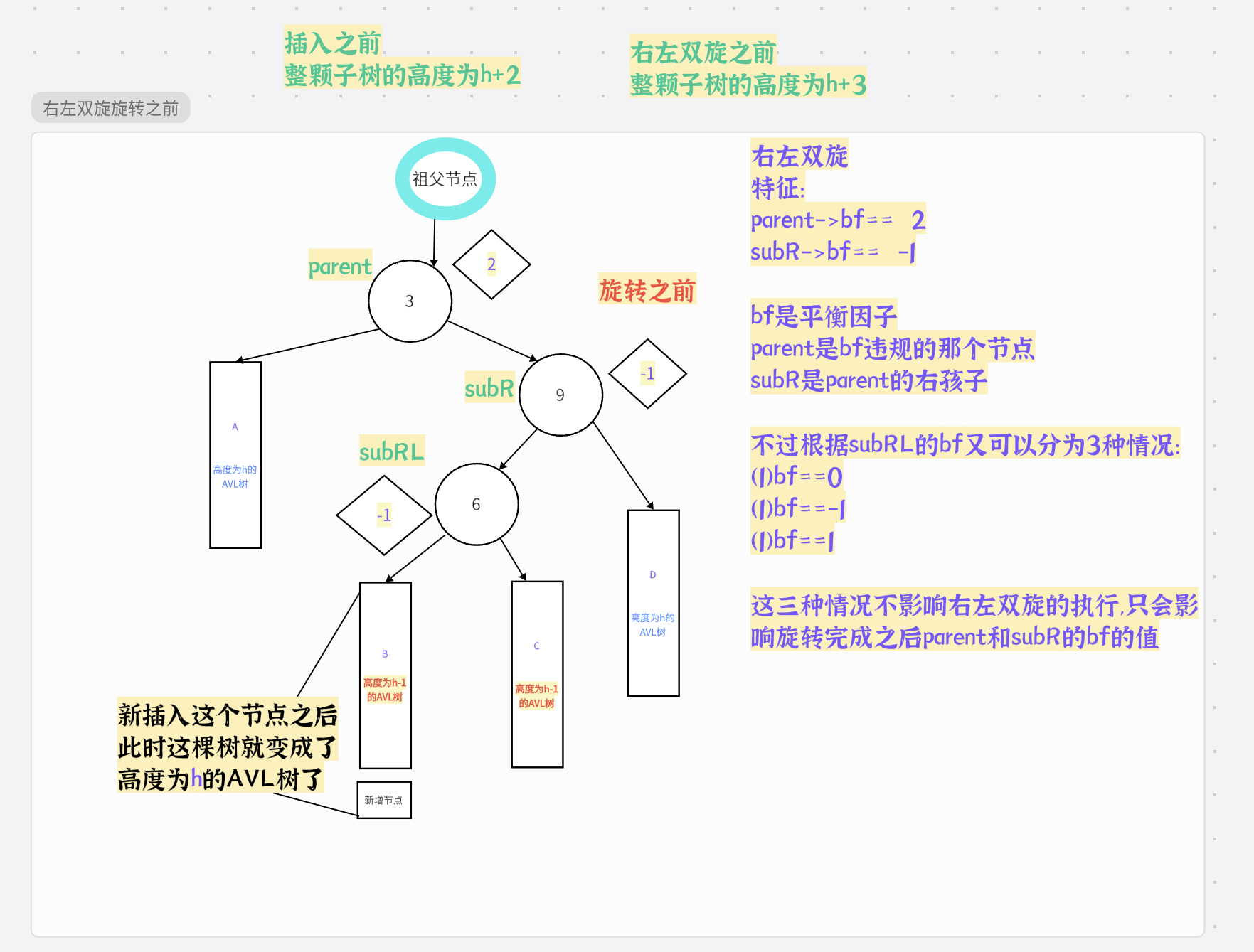
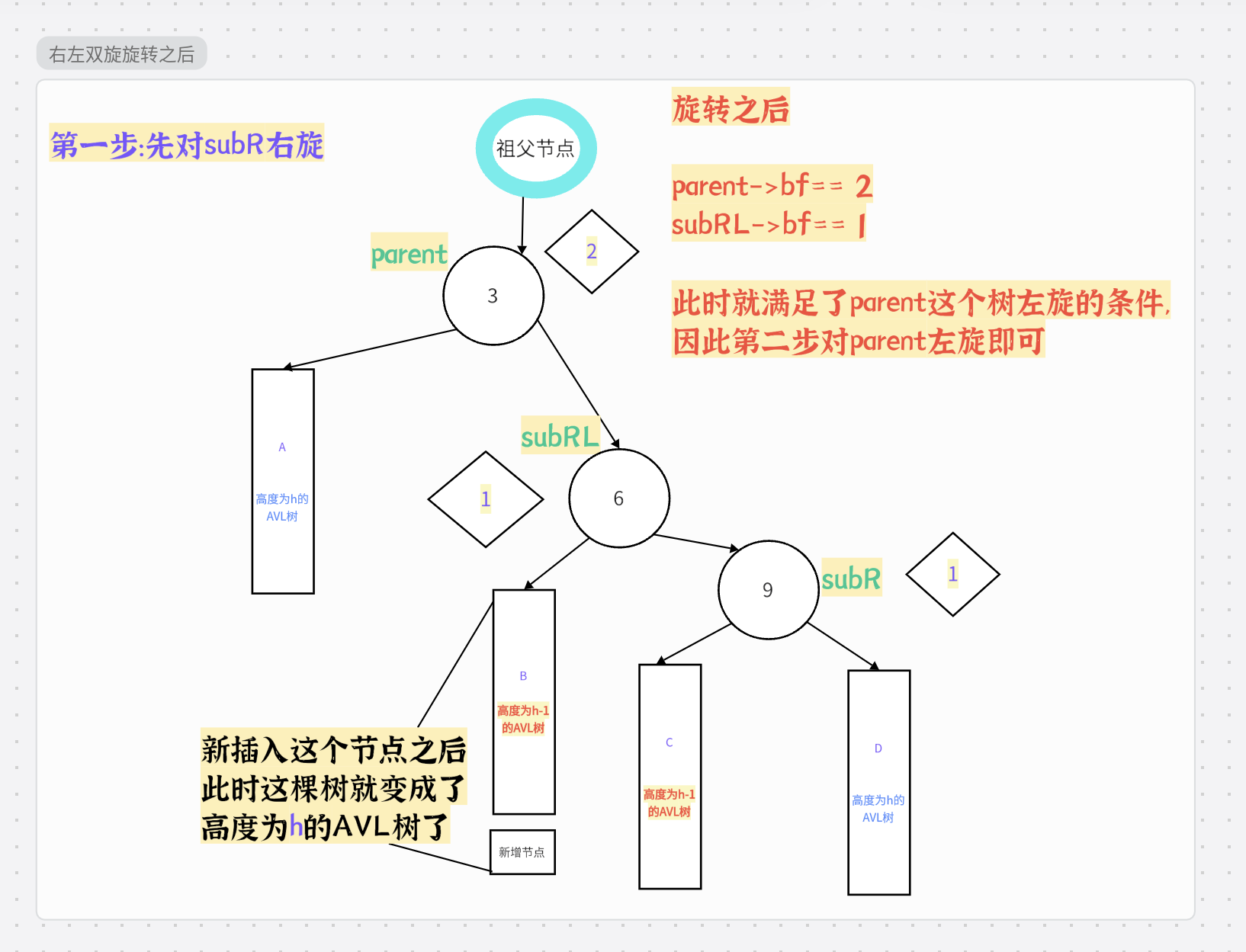
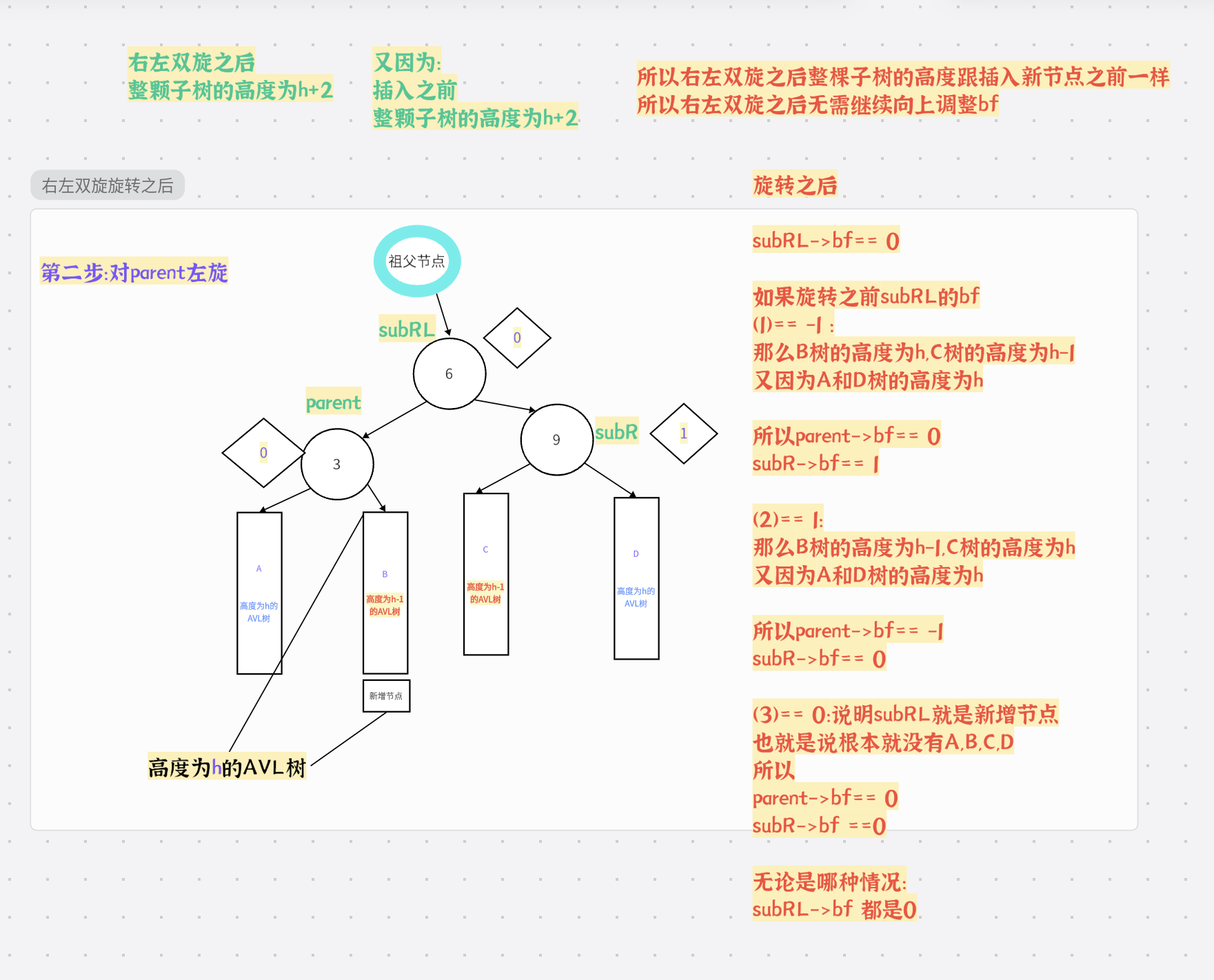
在这里插入图片描述

在这里插入图片描述
总结:

4.左右双旋的介绍

同理,左右双旋跟右单旋的基础条件也很像
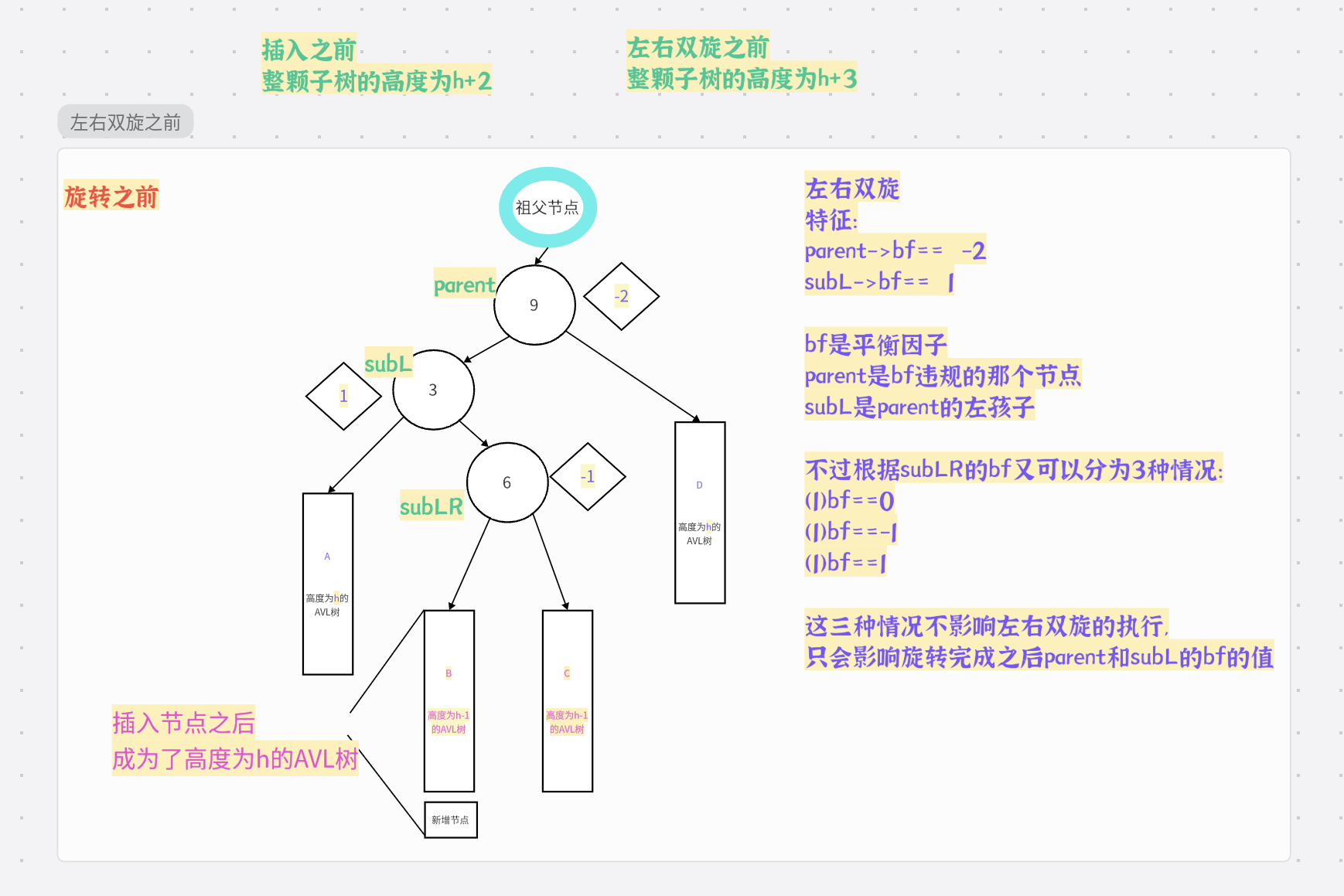
在这里插入图片描述

总结:

5.旋转条件的总结:

在这里插入图片描述

4.插入逻辑的完善

因此我们就能够写出这样的insert代码

// 在AVL树中插入值为data的节点
bool Insert(const pair<K,V>& data)
{
	if (_pRoot == nullptr)
	{
		_pRoot = new Node(data);
		return true;
	}
	Node* cur = _pRoot, * parent = nullptr;
	//1.找插入位置
	while (cur)
	{
		if (cur->_data > data)
		{
			parent = cur;
			cur = cur->_pLeft;
		}
		else if (cur->_data < data)
		{
			parent = cur;
			cur = cur->_pRight;
		}
		else
		{
			return false;
		}
	}
	//2.插入节点调整平衡因子
	cur = new Node(data);
	//在parent左边插入节点
	if (parent->_data > data)
	{
		parent->_pLeft = cur;
		parent->_bf--;
	}
	//在parent的右边插入节点
	else
	{
		parent->_pRight = cur;
		parent->_bf++;
	}
	cur->_pParent = parent;
	//3.向上影响平衡因子
	//影响的结束条件:
	//1.cur到达_pRoot,也就是parent到达nullptr
	//2.parent的bf调整之后变为0
	//因为0只能由1或者-1变过来
	//而且由1或者-1变成0时,parent这个树的高度没有发生变化,因此不会在往上去影响了
	//3.parent这棵树需要旋转
	//旋转之后会达到1个目的:
	//降低parent这棵树的高度,降为插入这个结点之前的高度
	//因此此时就不会在往上去影响了
	while (parent)
	{
		//此时无需在往上去影响
		if (parent->_bf == 0)
		{
			break;
		}
		//此时需要再往上去影响
		//因为1或者-1只能由0变过来,因此parent这个树的高度变高,需要往上去影响
		else if (parent->_bf == 1 || parent->_bf == -1)
		{
			cur = parent;
			parent = parent->_pParent;
			if (parent != nullptr)
			{
				//说明parent是左子树,因此会让祖父的bf--
				if (parent->_pLeft == cur)
				{
					parent->_bf--;
				}
				//说明parent是右子树,因此会让祖父的bf++
				else
				{
					parent->_bf++;
				}
			}
		}
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			//左单旋
			if (parent->_bf == 2 && cur->_bf == 1)
			{
				RotateL(parent);
			}
			//右左双旋
			else if (parent->_bf == 2 && cur->_bf == -1)
			{
				RotateRL(parent);
			}
			//右单旋
			else if (parent->_bf == -2 && cur->_bf == -1)
			{
				RotateR(parent);
			}
			//左右双旋
			else if (parent->_bf == -2 && cur->_bf == 1)
			{
				RotateLR(parent);
			}
			break;
		}
		else
		{
			assert(false);
		}
	}
	return true;
}

四.旋转的动图演示和代码实现

我们在上面已经介绍完什么是左、右单旋，右左、左右双旋转了
下面我们来看一下如何实现旋转呢?

1.左单旋

1.步骤+注意事项

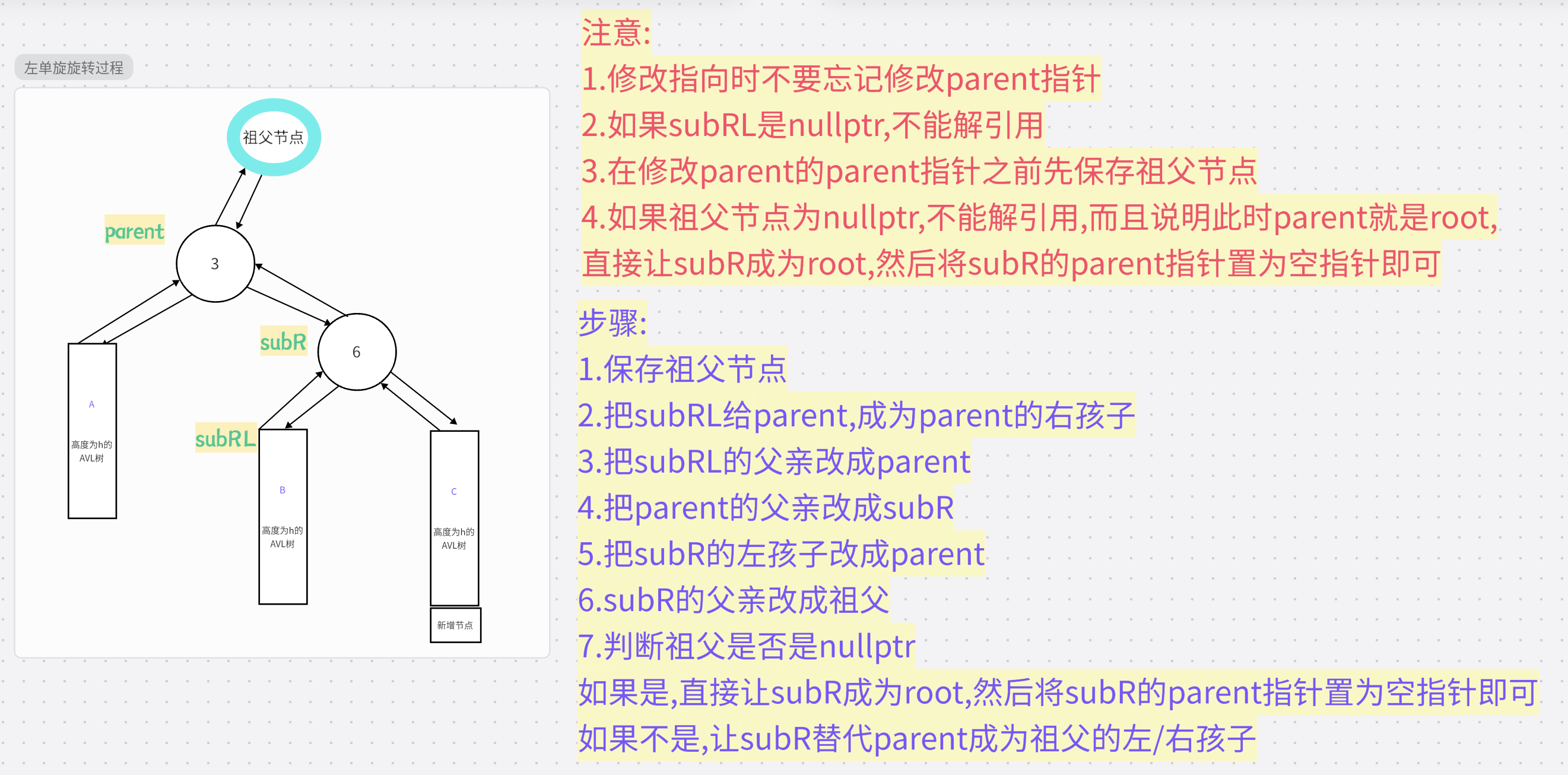
在这里插入图片描述

2.动图演示

旋转之前:
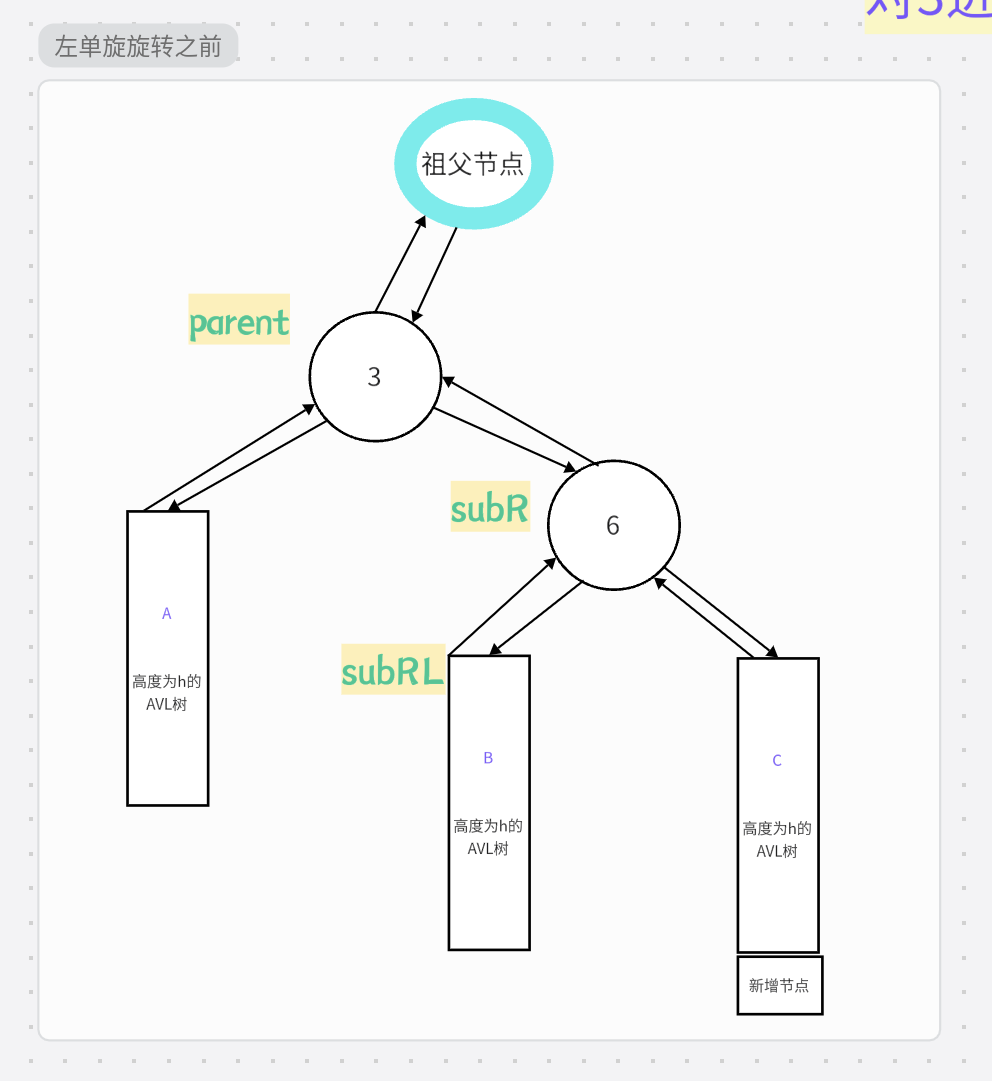
在这里插入图片描述
旋转过程:

旋转完成之后

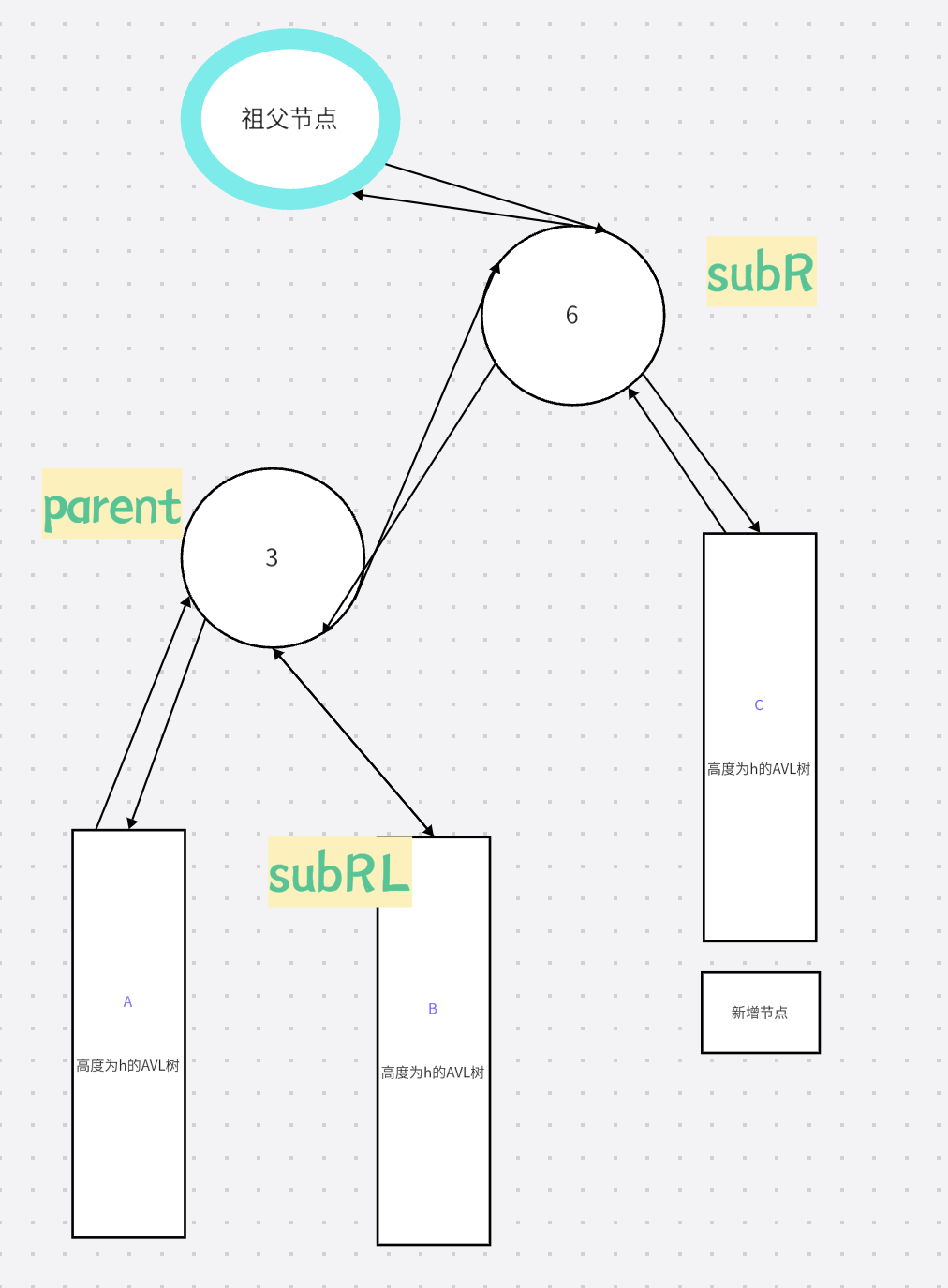
3.代码实现

// 左单旋
void RotateL(Node* pParent)
{
	Node* subR = pParent->_pRight;
	Node* subRL = subR->_pLeft;
	Node* grandParent = pParent->_pParent;
	pParent->_pParent = subR;
	subR->_pLeft = pParent;
	pParent->_pRight = subRL;
	if (subRL)
		subRL->_pParent = pParent;
	//说明此时pParent是_pRoot
	if (grandParent == nullptr)
	{
		_pRoot = subR;
		_pRoot->_pParent = nullptr;
	}
	//说明此时pParent所在的树是一颗子树,需要跟父亲链接
	else
	{
		if (pParent == grandParent->_pLeft)
		{
			grandParent->_pLeft = subR;
		}
		else
		{
			grandParent->_pRight = subR;
		}
		subR->_pParent = grandParent;
	}
	//调整平衡因子
	pParent->_bf = subR->_bf = 0;
}

2.右单旋

同理,右单旋也是类似的思路
而且注意事项跟左单旋如出一辙

1.动图演示

旋转之前：
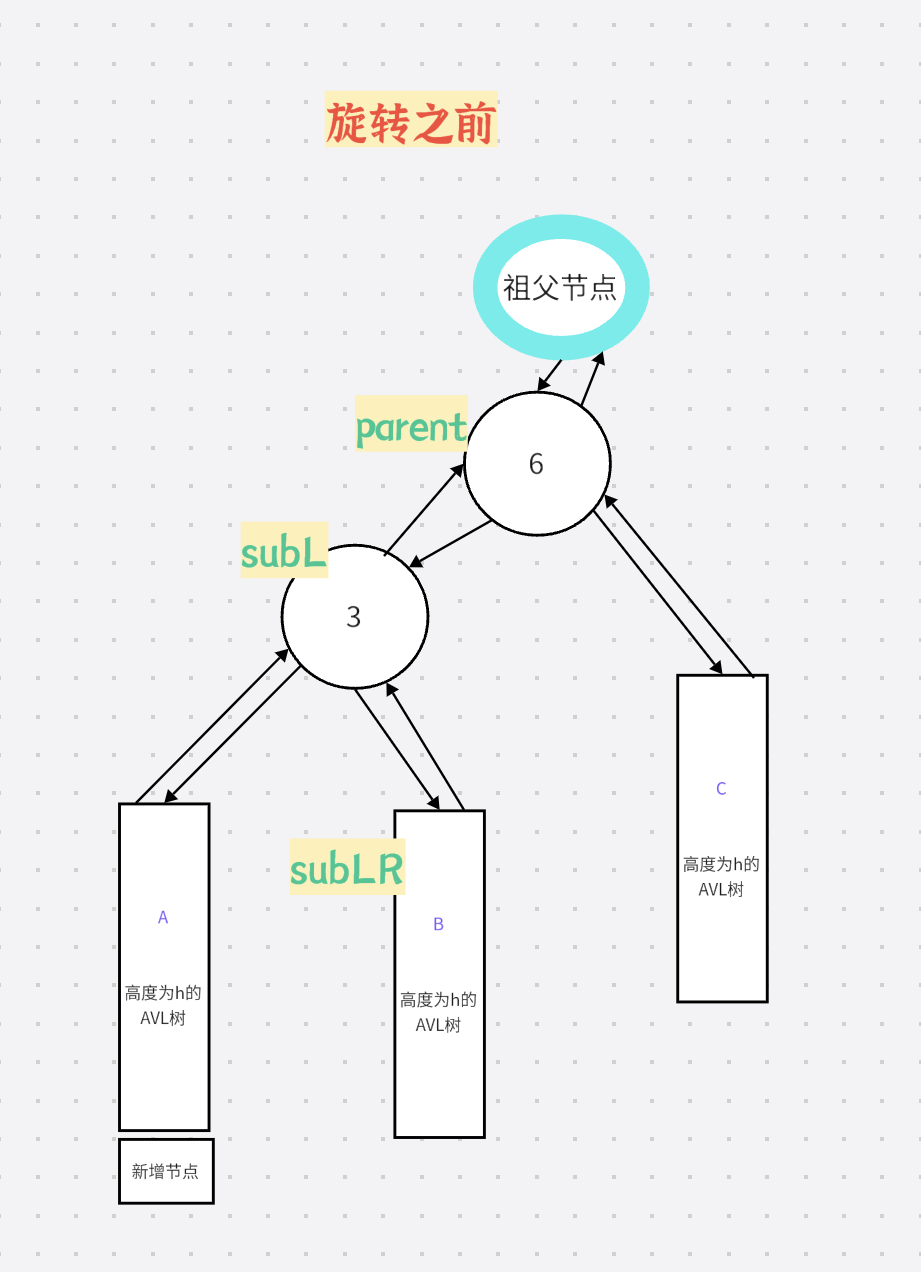
在这里插入图片描述
旋转过程：

旋转完成之后：

2.代码实现

// 右单旋
void RotateR(Node* pParent)
{
	Node* subL = pParent->_pLeft;
	Node* subLR = subL->_pRight;
	Node* grandParent = pParent->_pParent;
	subL->_pRight = pParent;
	pParent->_pParent = subL;
	pParent->_pLeft = subLR;
	if (subLR)
		subLR->_pParent = pParent;
	if (grandParent == nullptr)
	{
		_pRoot = subL;
		_pRoot->_pParent = nullptr;
	}
	else
	{
		if (pParent == grandParent->_pLeft)
		{
			grandParent->_pLeft = subL;
		}
		else
		{
			grandParent->_pRight = subL;
		}
		subL->_pParent = grandParent;
	}
	//修改平衡因子
	subL->_bf = pParent->_bf = 0;
}

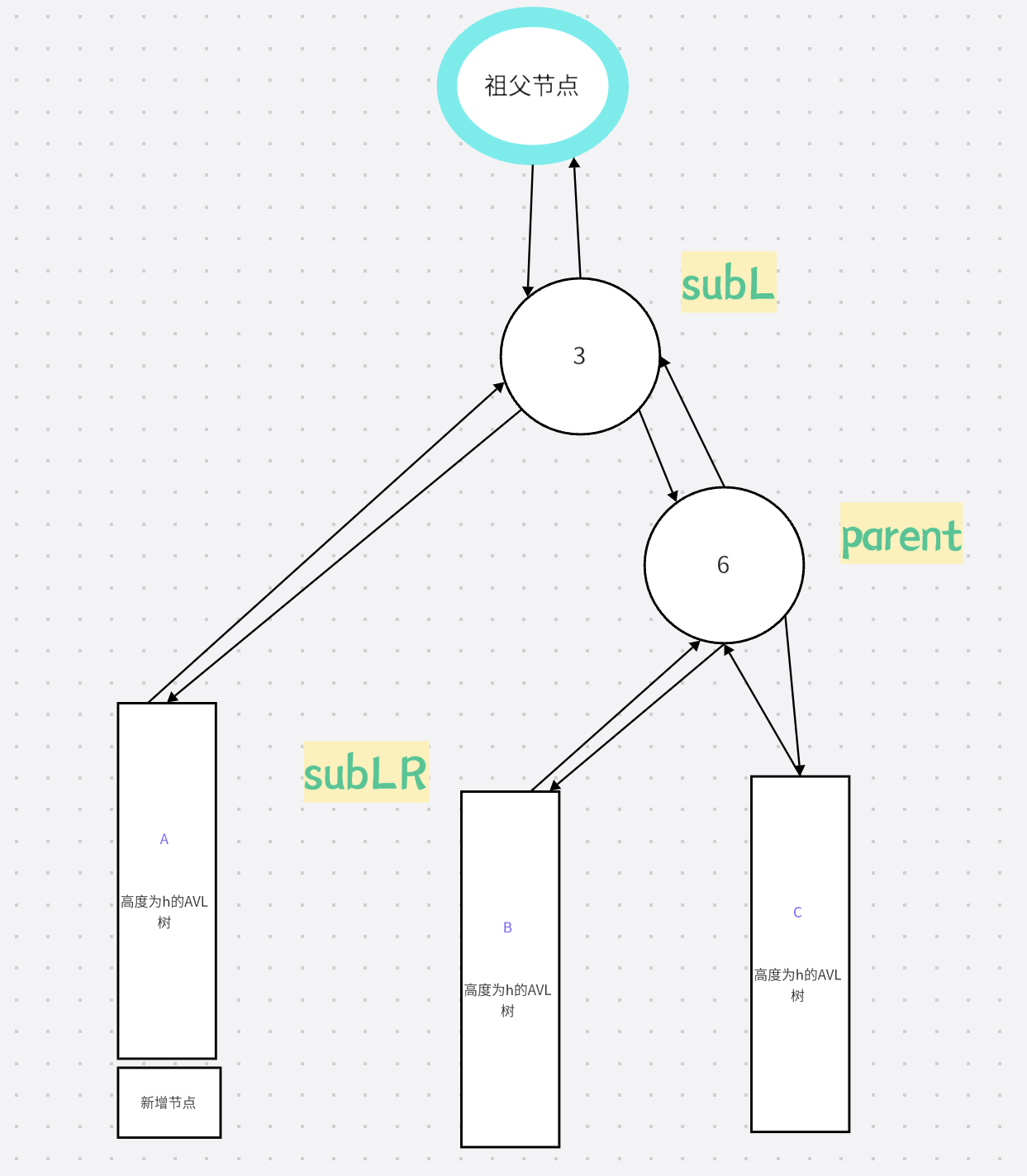
3.右左双旋

右左双旋和左右双旋都是对左单旋和右单旋的复用,这里就不在赘述了
直接上动图演示

1.先右旋

旋转之前：
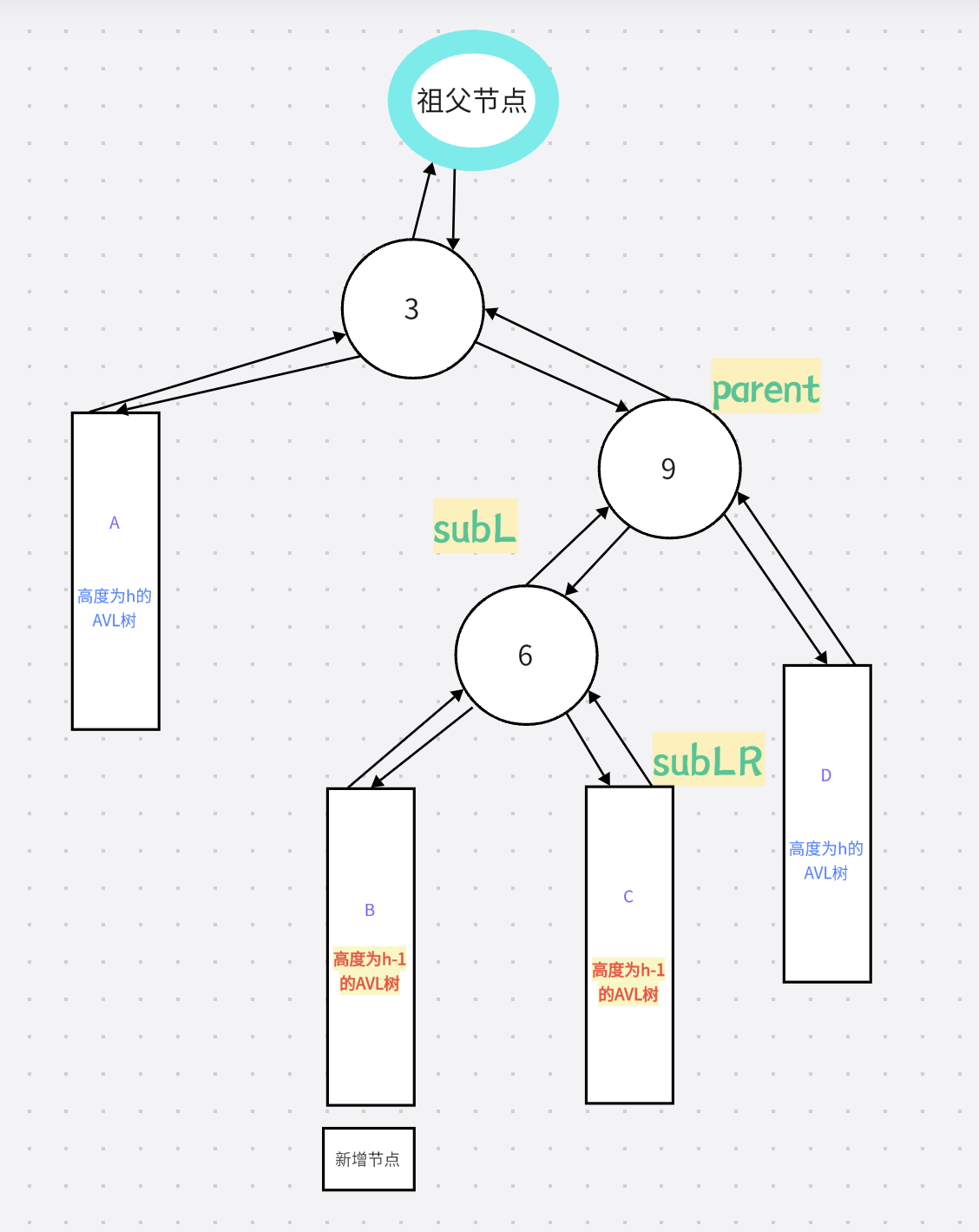
在这里插入图片描述
旋转过程:

旋转之后：

2.再左旋

旋转之前：
在这里插入图片描述
旋转过程:

旋转之后:

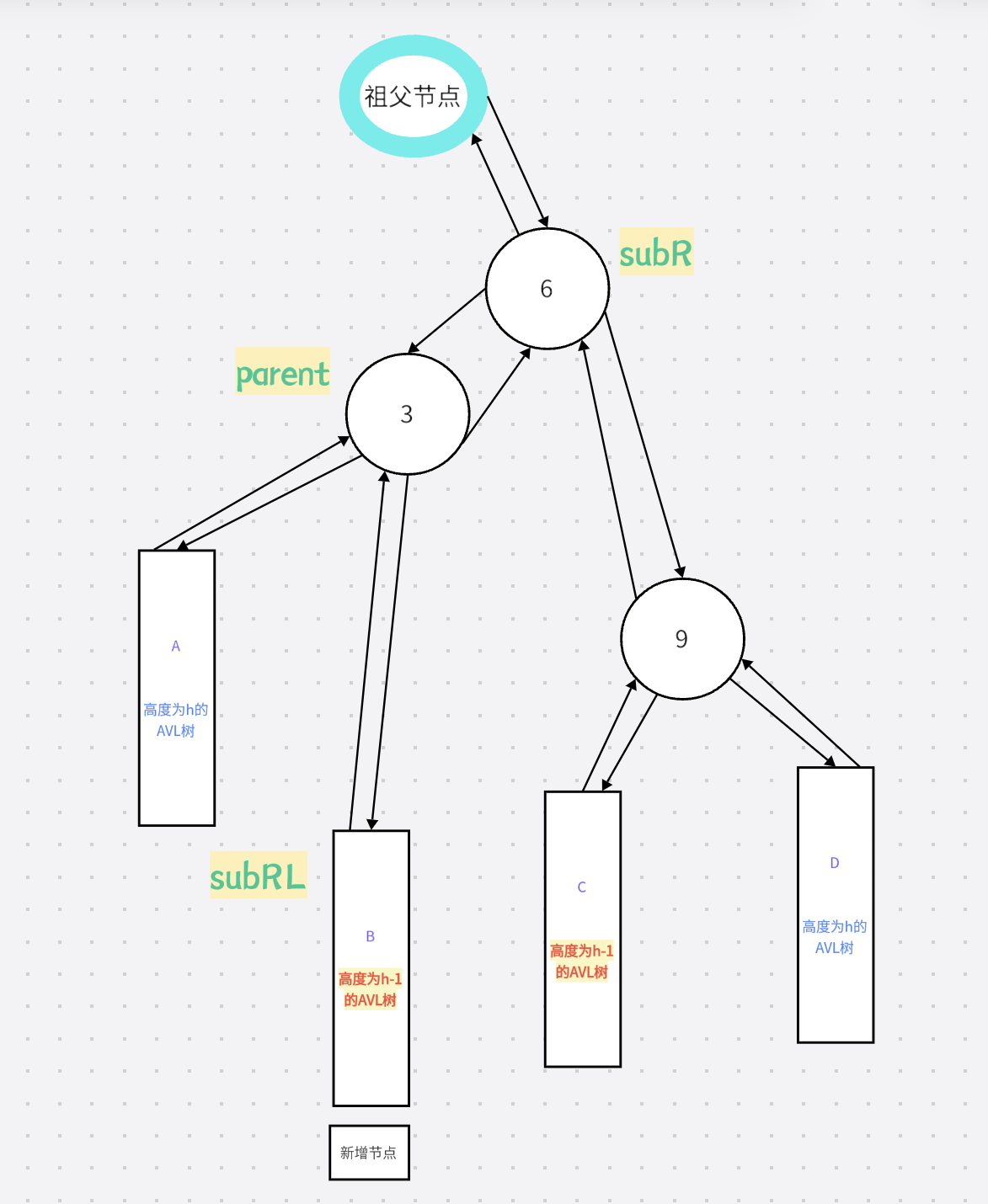
3.代码实现

// 右左双旋
void RotateRL(Node* pParent)
{
	Node* subR = pParent->_pRight;
	Node* subRL = subR->_pLeft;
	int bf = subRL->_bf;
	//对subR进行一次右旋
	RotateR(subR);
	//在对pParent进行一次左旋
	RotateL(pParent);
	//这两次旋转达到了一个目的:把subRL的左子树给pParent成为pParent的右子树
	//把subRL的右子树给subR成为subR的左子树

	//根据旋转前subRL的平衡因子调整平衡后的平衡因子
	if (bf == 0)
	{
		subR->_bf = pParent->_bf = subRL->_bf = 0;
	}
	//说明subRL的左子树更低
	else if (bf == 1)
	{
		pParent->_bf = -1;
		subR->_bf = subRL->_bf = 0;
	}
	else if (bf == -1)
	{
		subR->_bf = 1;
		pParent->_bf = subRL->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

4.左右双旋

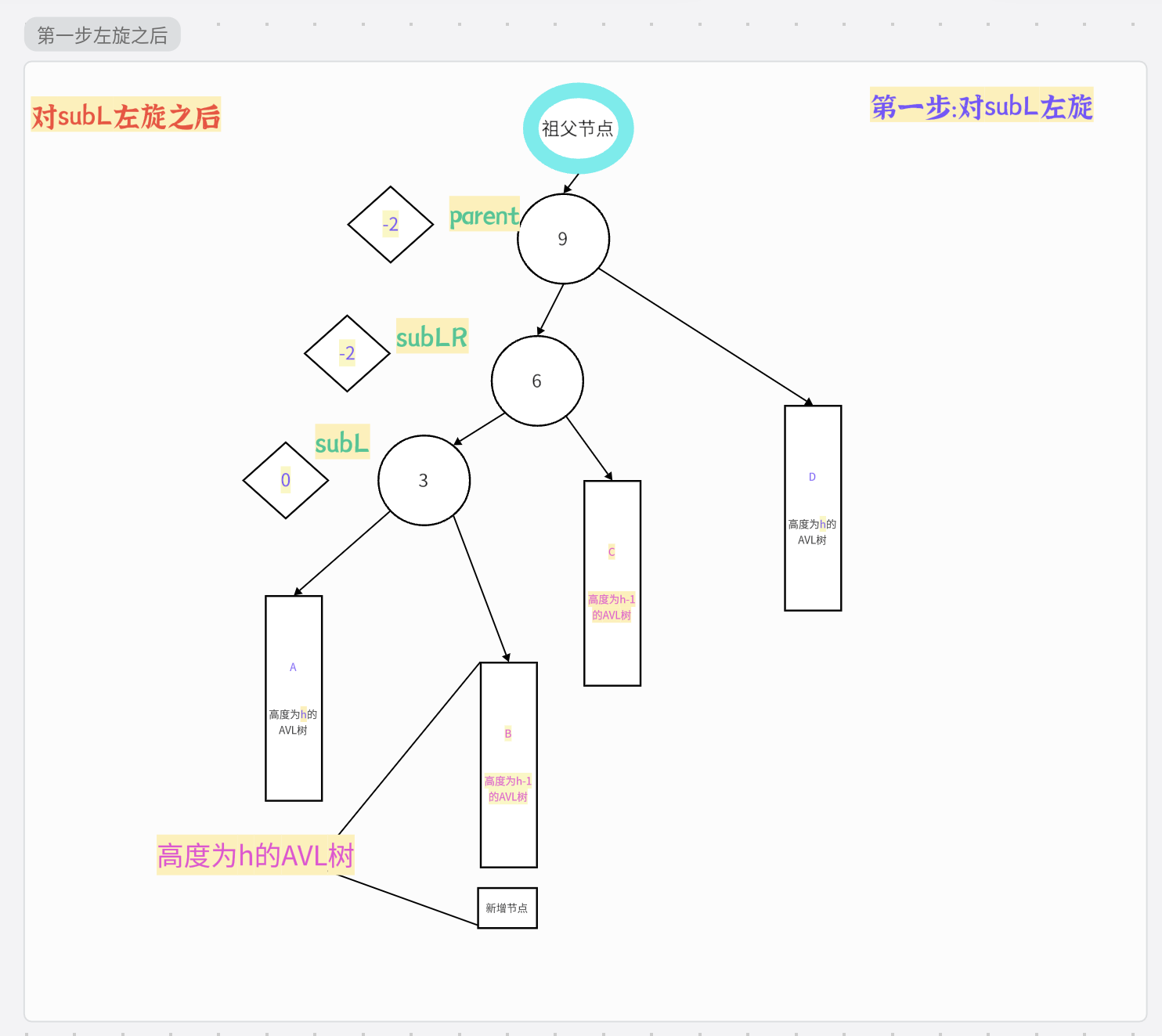
1.先左旋

旋转之前:
在这里插入图片描述
旋转过程:

旋转之后:

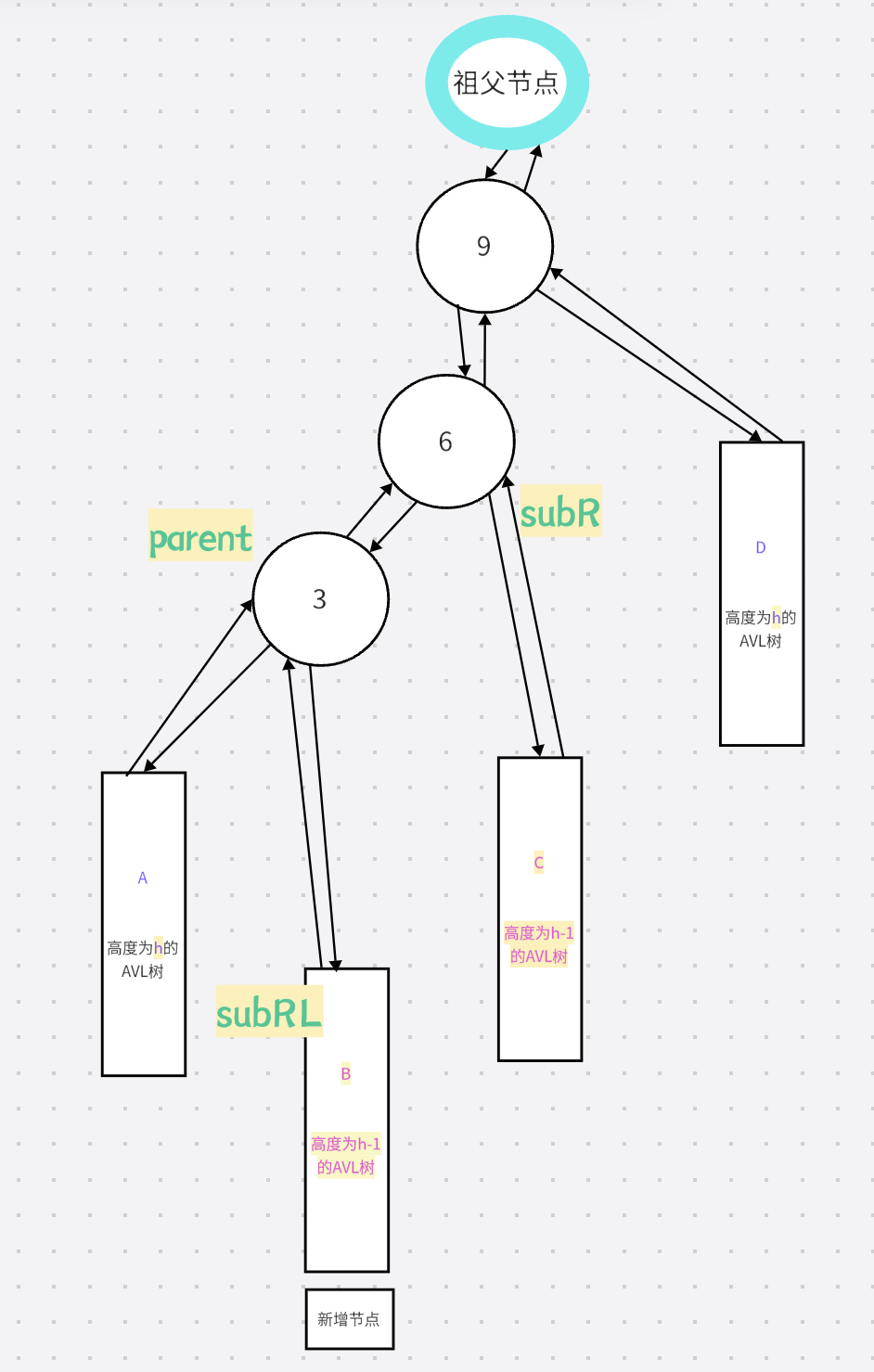
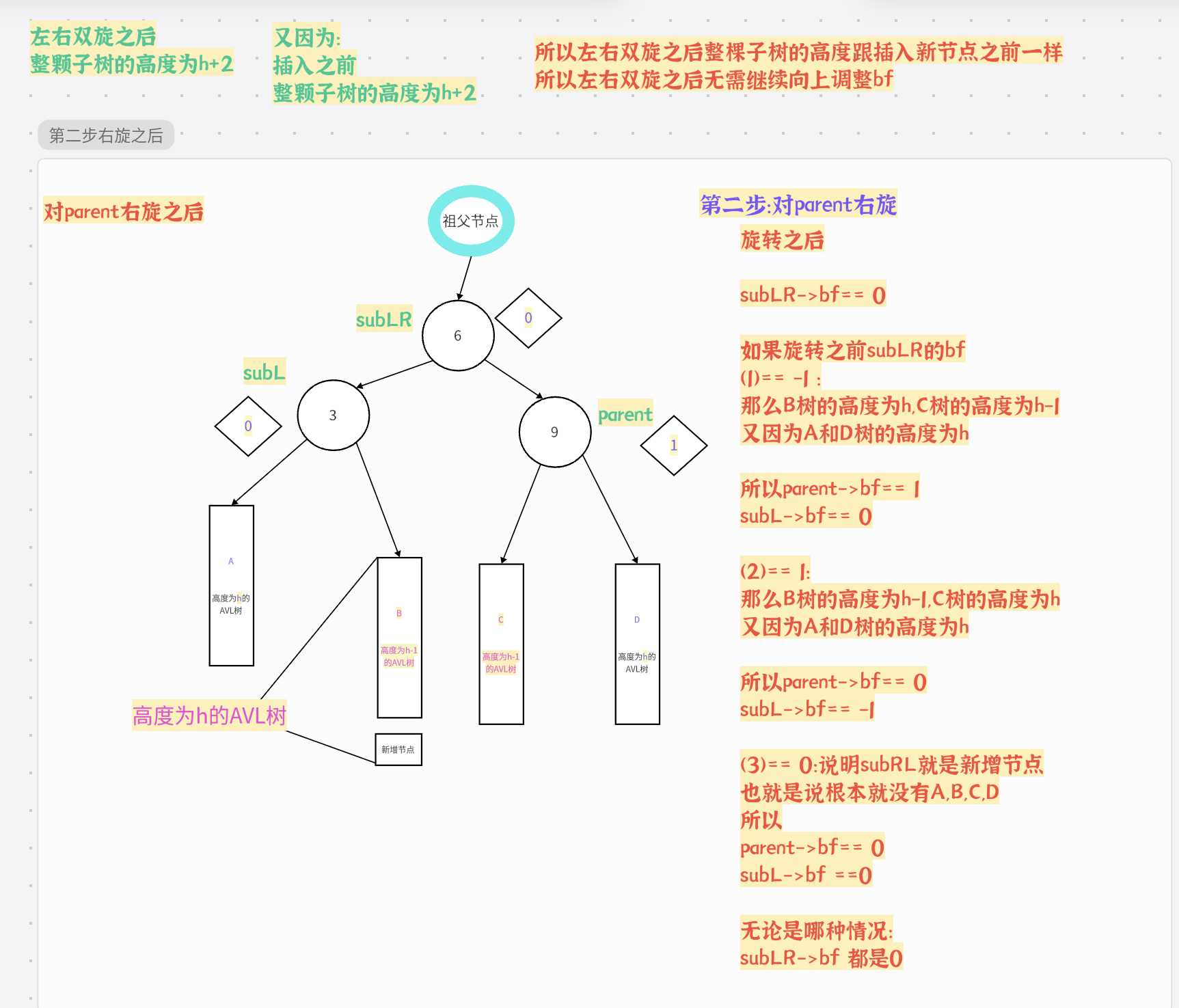
2.再右旋

旋转之前:
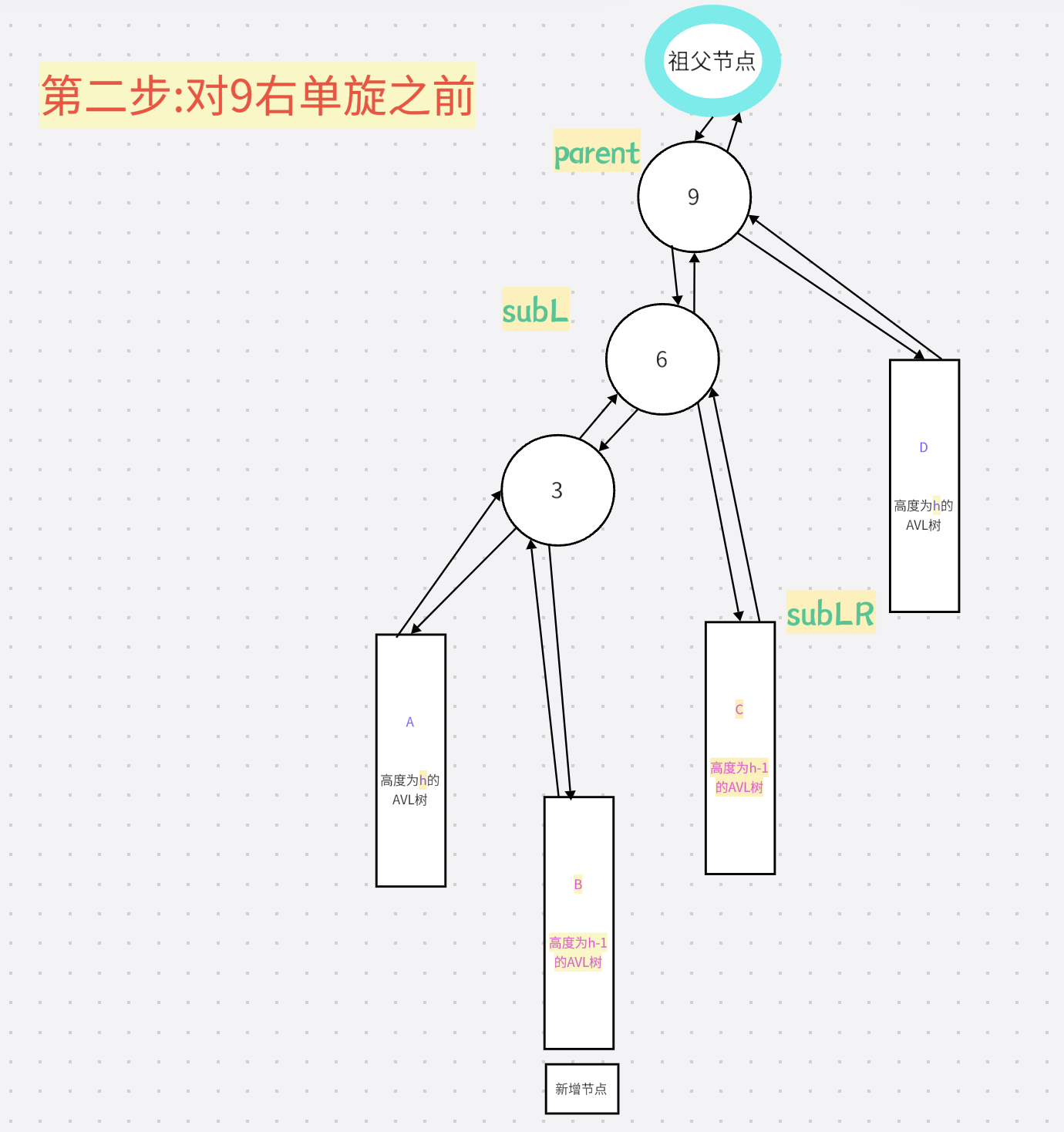
在这里插入图片描述
旋转过程:

旋转之后:

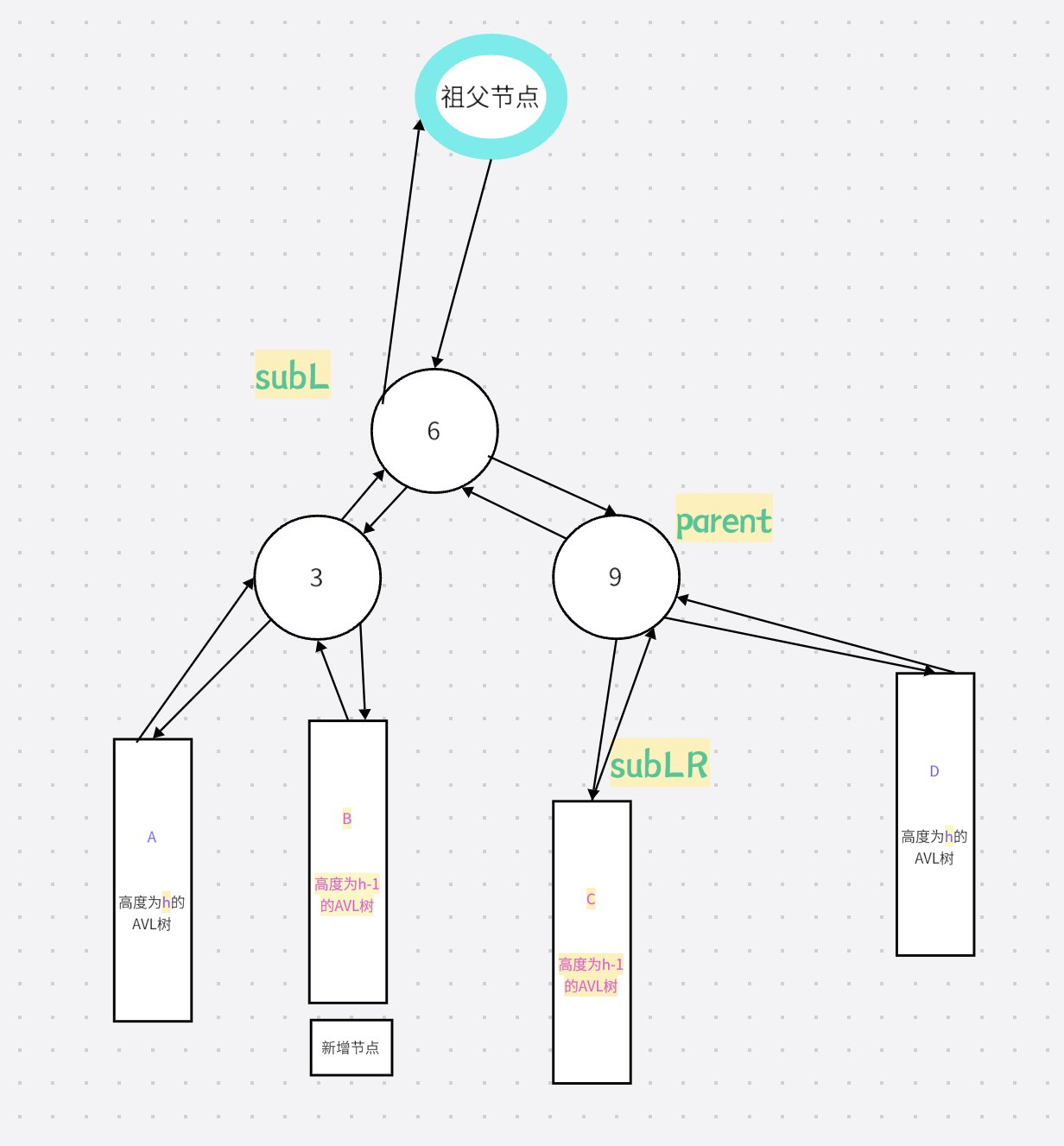
3.代码实现

// 左右双旋
void RotateLR(Node* pParent)
{
	Node* subL = pParent->_pLeft;
	Node* subLR = subL->_pRight;
	int bf = subLR->_bf;
	RotateL(subL);
	RotateR(pParent);
	//旋转的过程就是把subLR的左子树给subL成为subL的右子树
	//把subLR的右子树给pParent成为pParent的左子树
	if (bf == 0)
	{
		subL->_bf = subLR->_bf = pParent->_bf = 0;
	}
	else if (bf == 1)
	{
		subL->_bf = -1;
		subLR->_bf = pParent->_bf = 0;
	}
	else if (bf == -1)
	{
		pParent->_bf = 1;
		subL->_bf = subLR->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

五.AVL树的验证

为了验证AVL树的正确性
我们添加中序遍历代码,求高度代码,验证左右子树高度差不大于1的代码

// AVL树的验证
bool IsAVLTree()
{
	return _IsAVLTree(_pRoot);
}

void InOrder()
{
	_InOrder(_pRoot);
}

private:
void _InOrder(Node* root)
{
	if (root == nullptr) return;
	_InOrder(root->_pLeft);
	cout << root->_data.first << " " << root->_data.second << " ";
	_InOrder(root->_pRight);
}

// 根据AVL树的概念验证pRoot是否为有效的AVL树
bool _IsAVLTree(Node* pRoot)
{
	if (pRoot == nullptr) return true;
	int leftHeight = _Height(pRoot->_pLeft);
	int rightHeight = _Height(pRoot->_pRight);
	return abs(leftHeight - rightHeight) < 2 && _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
}

size_t _Height(Node* pRoot)
{
	if (pRoot == nullptr)
	{
		return 0;
	}
	int leftHeight = _Height(pRoot->_pLeft);
	int rightHeight = _Height(pRoot->_pRight);
	return max(leftHeight, rightHeight) + 1;
}

下面是测试代码

#include "AVLTree.h"
#include <vector>
int test1()
{
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVLTree<int,string> tree;
	for (auto& e : a)
	{
		cout << e << " : " << tree.Insert(make_pair(e,"wzs")) << endl;
	}
	cout << endl;
	tree.InOrder();
	cout << endl;
	cout << tree.IsAVLTree() << endl;
	return 0;
}
int test2()
{
	const int N = 300000;
	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
		//cout << v.back() << endl;
	}

	AVLTree<int,int> t;
	for (auto e : v)
	{
		if (e == 14604)
		{
			int x = 0;
		}

		t.Insert(make_pair(e,e));
		//cout << "Insert:" << e << "->" << t.IsAVLTree()<< endl;
	}

	cout << t.IsAVLTree() << endl;

	return 0;
}

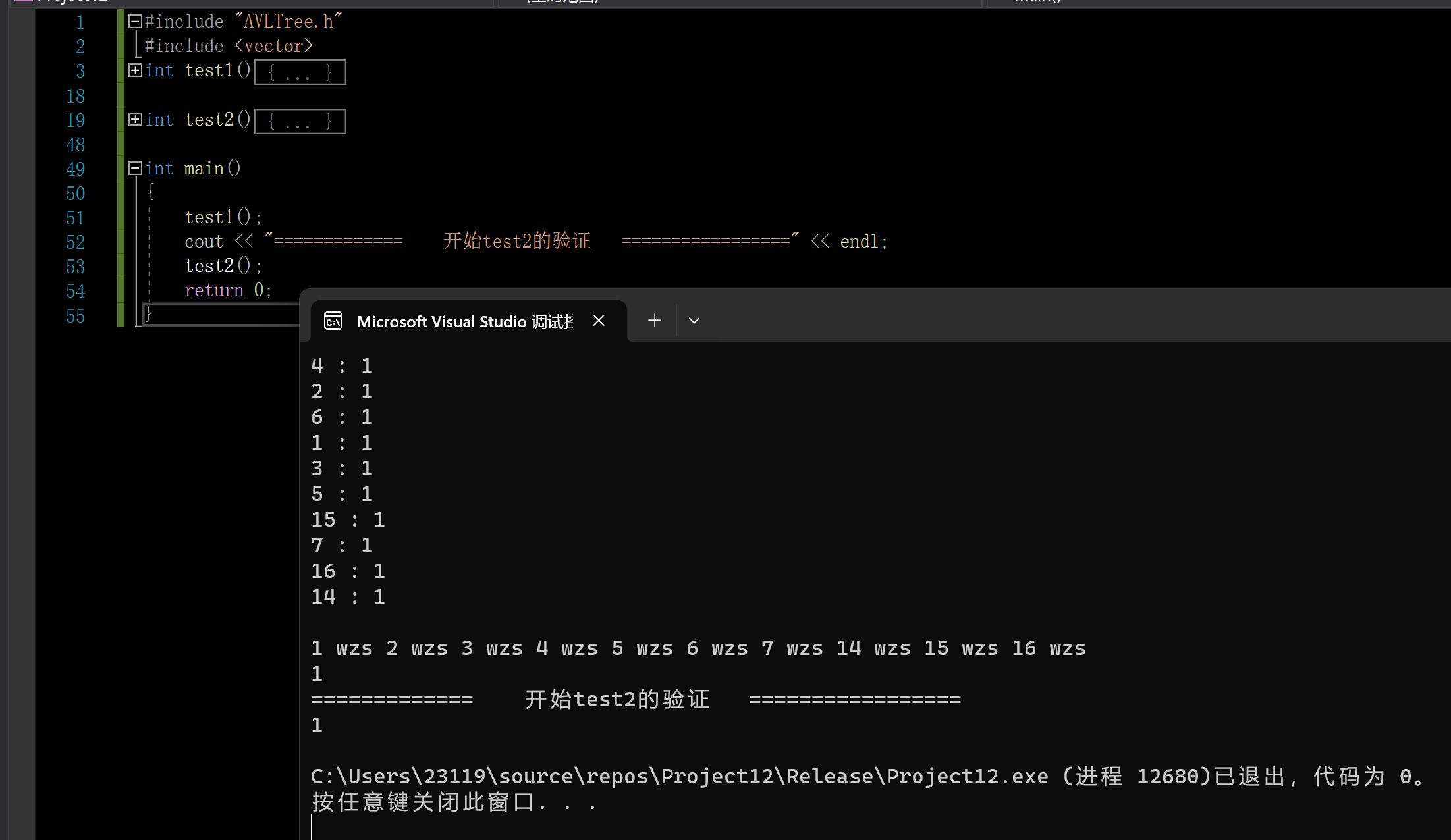
在这里插入图片描述
验证成功

六.完整代码

1.AVLTree.h:

#pragma once
#include <iostream>
using namespace std;
#include <assert.h>

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode(const pair<K,V>& data = pair<K,V>())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}
	AVLTreeNode<K,V>* _pLeft;
	AVLTreeNode<K,V>* _pRight;
	AVLTreeNode<K,V>* _pParent;
	pair<K,V> _data;
	int _bf;   // 节点的平衡因子
};


// AVL: 二叉搜索树 + 平衡因子的限制
template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	AVLTree()
		: _pRoot(nullptr)
	{}

	// 在AVL树中插入值为data的节点
	bool Insert(const pair<K,V>& data)
	{
		if (_pRoot == nullptr)
		{
			_pRoot = new Node(data);
			return true;
		}
		Node* cur = _pRoot, * parent = nullptr;
		//1.找插入位置
		while (cur)
		{
			if (cur->_data > data)
			{
				parent = cur;
				cur = cur->_pLeft;
			}
			else if (cur->_data < data)
			{
				parent = cur;
				cur = cur->_pRight;
			}
			else
			{
				return false;
			}
		}
		//2.插入节点调整平衡因子
		cur = new Node(data);
		//在parent左边插入节点
		if (parent->_data > data)
		{
			parent->_pLeft = cur;
			parent->_bf--;
		}
		//在parent的右边插入节点
		else
		{
			parent->_pRight = cur;
			parent->_bf++;
		}
		cur->_pParent = parent;
		//3.向上影响平衡因子
		//影响的结束条件:
		//1.cur到达_pRoot,也就是parent到达nullptr
		//2.parent的bf调整之后变为0
		//因为0只能由1或者-1变过来
		//而且由1或者-1变成0时,parent这个树的高度没有发生变化,因此不会在往上去影响了
		//3.parent这棵树需要旋转
		//旋转之后会达到1个目的:
		//降低parent这棵树的高度,降为插入这个结点之前的高度
		//因此此时就不会在往上去影响了
		while (parent)
		{
			//此时无需在往上去影响
			if (parent->_bf == 0)
			{
				break;
			}
			//此时需要再往上去影响
			//因为1或者-1只能由0变过来,因此parent这个树的高度变高,需要往上去影响
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_pParent;
				if (parent != nullptr)
				{
					//说明parent是左子树,因此会让祖父的bf--
					if (parent->_pLeft == cur)
					{
						parent->_bf--;
					}
					//说明parent是右子树,因此会让祖父的bf++
					else
					{
						parent->_bf++;
					}
				}
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//左单旋
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				//右左双旋
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}
				//右单旋
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				//左右双旋
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}

	// AVL树的验证
	bool IsAVLTree()
	{
		return _IsAVLTree(_pRoot);
	}

	void InOrder()
	{
		_InOrder(_pRoot);
	}

private:
	void _InOrder(Node* root)
	{
		if (root == nullptr) return;
		_InOrder(root->_pLeft);
		cout << root->_data.first << " " << root->_data.second << " ";
		_InOrder(root->_pRight);
	}

	// 根据AVL树的概念验证pRoot是否为有效的AVL树
	bool _IsAVLTree(Node* pRoot)
	{
		if (pRoot == nullptr) return true;
		int leftHeight = _Height(pRoot->_pLeft);
		int rightHeight = _Height(pRoot->_pRight);
		return abs(leftHeight - rightHeight) < 2 && _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
	}

	size_t _Height(Node* pRoot)
	{
		if (pRoot == nullptr)
		{
			return 0;
		}
		int leftHeight = _Height(pRoot->_pLeft);
		int rightHeight = _Height(pRoot->_pRight);
		return max(leftHeight, rightHeight) + 1;
	}

	// 右单旋
	void RotateR(Node* pParent)
	{
		Node* subL = pParent->_pLeft;
		Node* subLR = subL->_pRight;
		Node* grandParent = pParent->_pParent;
		subL->_pRight = pParent;
		pParent->_pParent = subL;
		pParent->_pLeft = subLR;
		if (subLR)
			subLR->_pParent = pParent;
		if (grandParent == nullptr)
		{
			_pRoot = subL;
			_pRoot->_pParent = nullptr;
		}
		else
		{
			if (pParent == grandParent->_pLeft)
			{
				grandParent->_pLeft = subL;
			}
			else
			{
				grandParent->_pRight = subL;
			}
			subL->_pParent = grandParent;
		}
		//修改平衡因子
		subL->_bf = pParent->_bf = 0;
	}

	// 左单旋
	void RotateL(Node* pParent)
	{
		Node* subR = pParent->_pRight;
		Node* subRL = subR->_pLeft;
		Node* grandParent = pParent->_pParent;
		pParent->_pParent = subR;
		subR->_pLeft = pParent;
		pParent->_pRight = subRL;
		if (subRL)
			subRL->_pParent = pParent;
		//说明此时pParent是_pRoot
		if (grandParent == nullptr)
		{
			_pRoot = subR;
			_pRoot->_pParent = nullptr;
		}
		//说明此时pParent所在的树是一颗子树,需要跟父亲链接
		else
		{
			if (pParent == grandParent->_pLeft)
			{
				grandParent->_pLeft = subR;
			}
			else
			{
				grandParent->_pRight = subR;
			}
			subR->_pParent = grandParent;
		}
		//调整平衡因子
		pParent->_bf = subR->_bf = 0;
	}

	// 右左双旋
	void RotateRL(Node* pParent)
	{
		Node* subR = pParent->_pRight;
		Node* subRL = subR->_pLeft;
		int bf = subRL->_bf;
		//对subR进行一次右旋
		RotateR(subR);
		//在对pParent进行一次左旋
		RotateL(pParent);
		//这两次旋转达到了一个目的:把subRL的左子树给pParent成为pParent的右子树
		//把subRL的右子树给subR成为subR的左子树

		//根据旋转前subRL的平衡因子调整平衡后的平衡因子
		if (bf == 0)
		{
			subR->_bf = pParent->_bf = subRL->_bf = 0;
		}
		//说明subRL的左子树更低
		else if (bf == 1)
		{
			pParent->_bf = -1;
			subR->_bf = subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			subR->_bf = 1;
			pParent->_bf = subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	// 左右双旋
	void RotateLR(Node* pParent)
	{
		Node* subL = pParent->_pLeft;
		Node* subLR = subL->_pRight;
		int bf = subLR->_bf;
		RotateL(subL);
		RotateR(pParent);
		//旋转的过程就是把subLR的左子树给subL成为subL的右子树
		//把subLR的右子树给pParent成为pParent的左子树
		if (bf == 0)
		{
			subL->_bf = subLR->_bf = pParent->_bf = 0;
		}
		else if (bf == 1)
		{
			subL->_bf = -1;
			subLR->_bf = pParent->_bf = 0;
		}
		else if (bf == -1)
		{
			pParent->_bf = 1;
			subL->_bf = subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

private:
	Node* _pRoot;
};

2.test.cpp

#include "AVLTree.h"
#include <vector>
int test1()
{
	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVLTree<int,string> tree;
	for (auto& e : a)
	{
		cout << e << " : " << tree.Insert(make_pair(e,"wzs")) << endl;
	}
	cout << endl;
	tree.InOrder();
	cout << endl;
	cout << tree.IsAVLTree() << endl;
	return 0;
}

int test2()
{
	const int N = 300000;
	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand() + i);
		//cout << v.back() << endl;
	}

	AVLTree<int,int> t;
	for (auto e : v)
	{
		if (e == 14604)
		{
			int x = 0;
		}

		t.Insert(make_pair(e,e));
		//cout << "Insert:" << e << "->" << t.IsAVLTree()<< endl;
	}

	cout << t.IsAVLTree() << endl;

	return 0;
}

int main()
{
	test1();
	cout << "=============    开始test2的验证   =================" << endl;
	test2();
	return 0;
}

以上就是C++ AVL树(四种旋转,插入)的全部内容,希望能对大家有所帮助!

文章来源:https://blog.csdn.net/Wzs040810/article/details/135099616
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！