【面试高频算法解析】算法练习5 深度优先搜索

前言

本专栏旨在通过分类学习算法，使您能够牢固掌握不同算法的理论要点。通过策略性地练习精选的经典题目，帮助您深度理解每种算法，避免出现刷了很多算法题，还是一知半解的状态

---

专栏导航

1. 二分查找
2. 回溯
3. 双指针
4. 滑动窗口
5. 深度优先搜索
6. 广度优先搜索

---

算法解析

深度优先搜索（Depth-First Search，简称 DFS）是一种用于遍历或搜索树、图结构的算法。与广度优先搜索不同，深度优先搜索会尽可能深地遍历图的分支，直到到达末端，然后回溯到上一个分叉点，继续探索未被遍历的分支。

DFS 可以通过递归或栈数据结构来实现。递归实现的代码结构较为简洁，而非递归实现则使用栈来模拟递归过程。以下是 DFS 的基本步骤：

1. 选择起点：从一个起点节点开始遍历。

2. 访问节点：访问当前节点，并将其标记为已访问。

3. 递归遍历邻居：对于当前节点的每一个未访问的邻居节点，递归地调用 DFS 方法。

4. 回溯：当当前节点的所有邻居都被访问后，回溯到上一个节点，继续执行步骤3。

5. 重复：重复上述步骤，直到所有从起点可达的节点都被访问。

DFS 的特点是优先沿着一条路径深入探索，直到尽头后再回溯。这种特性使得 DFS 不仅适用于求解路径问题，还常用于拓扑排序、连通性检测、求解迷宫等问题。

以下是一个使用递归实现 DFS 的 Python 示例：

def dfs(graph, node, visited):
    if node not in visited:
        print(node)  # 可以在这里处理节点
        visited.add(node)  # 将节点标记为已访问
        for neighbor in graph[node]:
            dfs(graph, neighbor, visited)  # 递归访问邻居节点

# 示例图
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 创建一个集合，用于存储已访问的节点
visited = set()

# 从节点 'A' 开始 DFS
dfs(graph, 'A', visited)

在这个示例中，我们定义了一个图的邻接表表示，并使用递归方法实现了 DFS 算法。当我们从节点 ‘A’ 开始遍历图时，算法会深入访问每个节点，直到所有节点都被探索到。这里的 visited 集合用于记录已经访问过的节点，以防止节点被重复访问。

---

实战练习

省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

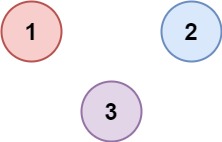
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

官方题解

---

岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出：1

示例 2：
输入：grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出：3

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

官方题解

---