LeetCode 144. 94. 145. 二叉树的前序，中序，后续遍历（详解） ? ?)?*??

经过前面的二叉树的学习，现在让我们实操来练练手~如果对二叉树还不熟悉的小伙伴可以看看我的这篇博客~数据结构——二叉树（先序、中序、后序及层次四种遍历（C语言版））超详细~ (???) Q_Q-CSDN博客

?

144.二叉树的前序遍历

题目描述:

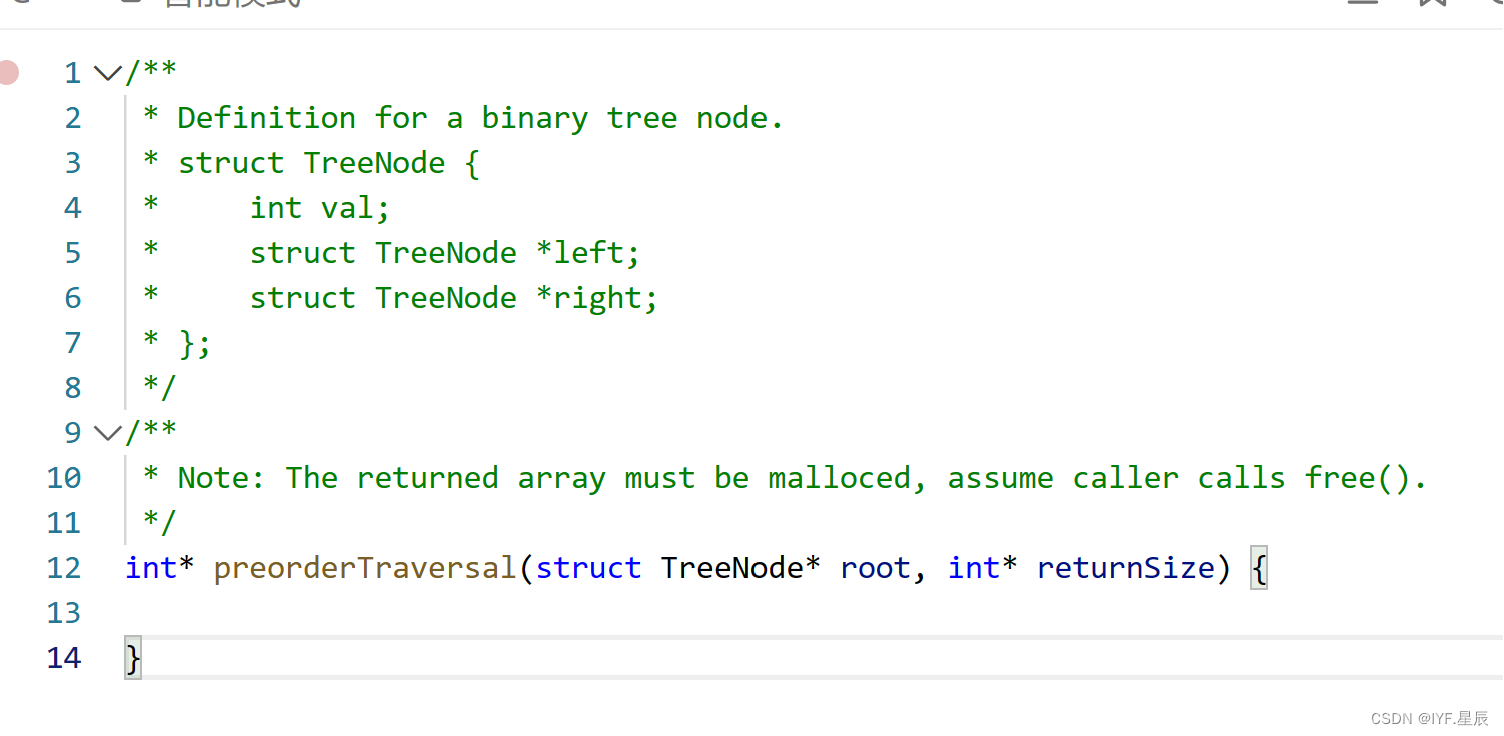
题目让我们返回节点值的前序遍历，让我们一起看看题目所给的代码：

?

?函数的定义与功能:

1.定义一个TreeSize函数用于计算这颗数的节点个数

2.preOrderTree函数用于进行前序遍历

3.preorderTraversal，也就是题目所给的函数用于返回遍历后的数组大小和树的节点个数?

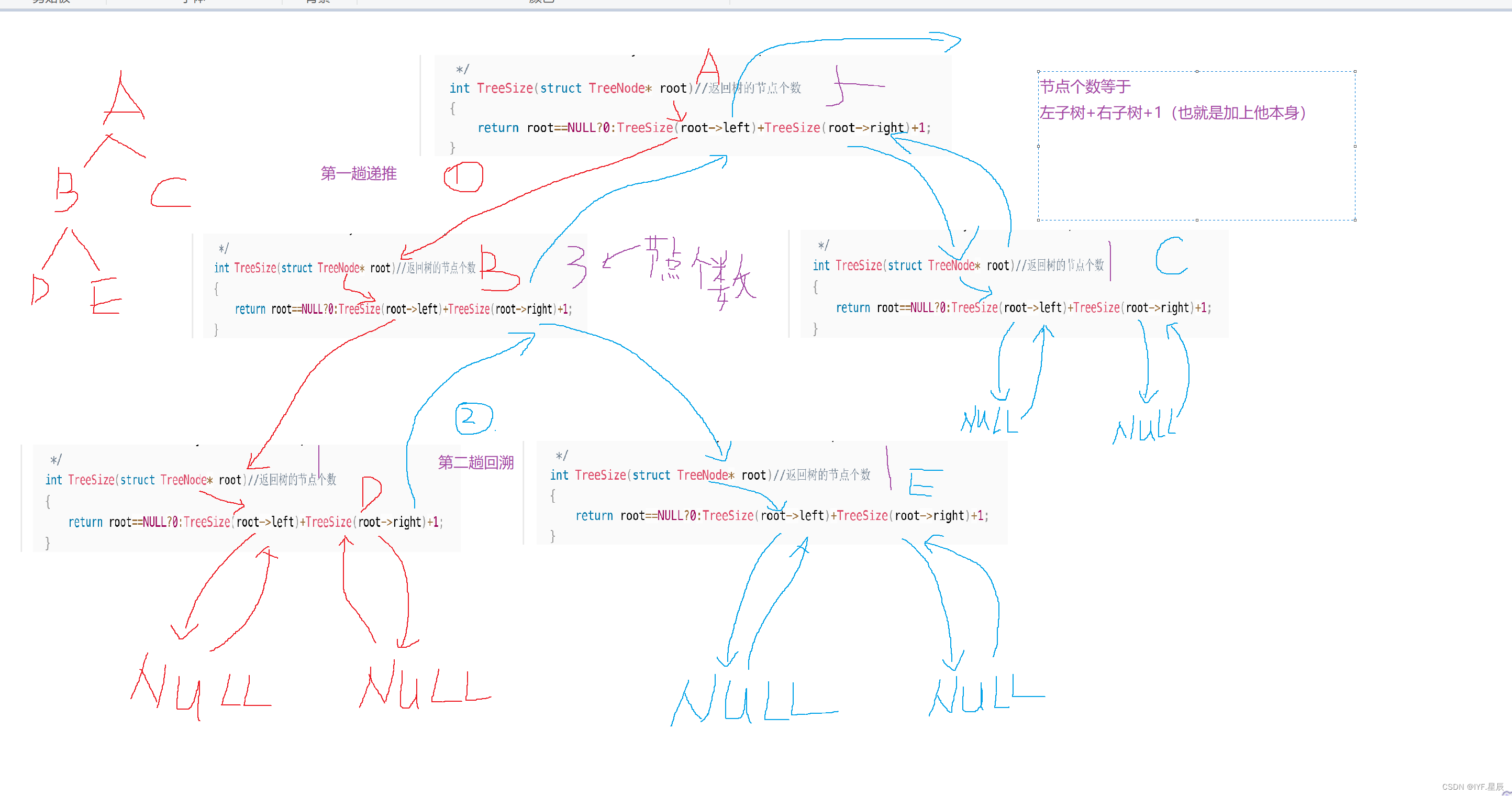
一. TreeSize函数的实现：

int TreeSize(struct TreeNode* root)//返回树的节点个数
{
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}

?通过判断根节点是否为空，来进行递归操作。直到将这个问题划分为一个不可再分的子问题，即根的左子树加右子树的个数在加上本身，也就是+1。具体方式见下图（函数的递归展开图）这里假设所构建的数如图所示：

二.?preOrderTree函数的实现：

?这里注意是通过改变*pi的值来实现数组下标的移位，同时a也是我们要返回的数组。

void preOrderTree(struct TreeNode* root,int* a,int* pi)//前序遍历
{
    if(root==NULL)//如果节点为空就返回空
    return;
    a[*pi]=root->val;//给要返回的数组赋予二叉树中的值
    ++(*pi);//通过pi来实现数组元素的移位问题
    preOrderTree(root->left,a,pi);
    preOrderTree(root->right,a,pi);
}

三.preorderTraversal函数的实现：

这里开创一个大小为size的数组，用于存储要返回的值

int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    int size=TreeSize(root);
    int* a=(int*)malloc(size*sizeof(int));//为数组申请一片size大小的空间
    int i=0;
    preOrderTree(root,a,&i);
    *returnSize=size;
    return a;
}

?最后完整代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)//返回树的节点个数
{
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void preOrderTree(struct TreeNode* root,int* a,int* pi)//前序遍历
{
    if(root==NULL)//如果节点为空就返回空
    return;
    a[*pi]=root->val;//给要返回的数组赋予二叉树中的值
    ++(*pi);//通过pi来实现数组元素的移位问题
    preOrderTree(root->left,a,pi);
    preOrderTree(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    int size=TreeSize(root);
    int* a=(int*)malloc(size*sizeof(int));//为数组申请一片size大小的空间
    int i=0;
    preOrderTree(root,a,&i);
    *returnSize=size;
    return a;
}

这里中序与后续遍历的过程与前序基本一致，就是In(post)OrderTree中对数组的赋值的位置移到了In(post)OrderTree（root->left,a,pi）的中间与后面。这里就不在赘述。直接上代码：

94.二叉树的中序遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)//返回树的节点个数
{
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void inorderTree(struct TreeNode* root,int* a,int* pi)
{
    if(root==NULL)
    return;
    inorderTree(root->left,a,pi);
    a[*pi]=root->val;
    ++(*pi);
    inorderTree(root->right,a,pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
    int size=TreeSize(root);
    int* a=(int*)malloc(size*sizeof(int));
    int i=0;
    inorderTree(root,a,&i);
    *returnSize=size;
    return a;
}

?145.二叉树的后续遍历：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int TreeSize(struct TreeNode* root)
{
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void postorderTree(struct TreeNode* root,int* a,int* pi)
{
    if(root==NULL)
    return;
    postorderTree(root->left,a,pi);
    postorderTree(root->right,a,pi);
    a[*pi]=root->val;
    ++(*pi);
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
    int size=TreeSize(root);
    int* a=(int*)malloc(size*sizeof(int));
    int i=0;
    postorderTree(root,a,&i);
    *returnSize=size;
    return a;
}

博客到这里也是结束了，喜欢的小伙伴可以点赞加关注支持下博主，这对我真的很重要~~

?