20240112-确定字符串的两半是否相似
发布时间:2024年01月13日
题目要求
给定一个偶数长度的字符串s。把这个字符串分成长度相等的两半,前半部分a,后半部分b。
如果两个字符串的元音字母数目相同('a'、'e'、'i'、'o'、'u'、'A'、'E'、'I'、'O'、'U'),那么它们就是相同的。区分大小写。
如果a和b相同,则返回true,否则返回false。
思路
双指针,两个map解决。时间复杂度O(n)。不需要用到map,因为只需要统计元音字母的总数量,不需要区分不同的元音字母,两个count前后计数即可。然后用一个set来存储需要查找的元音字母。
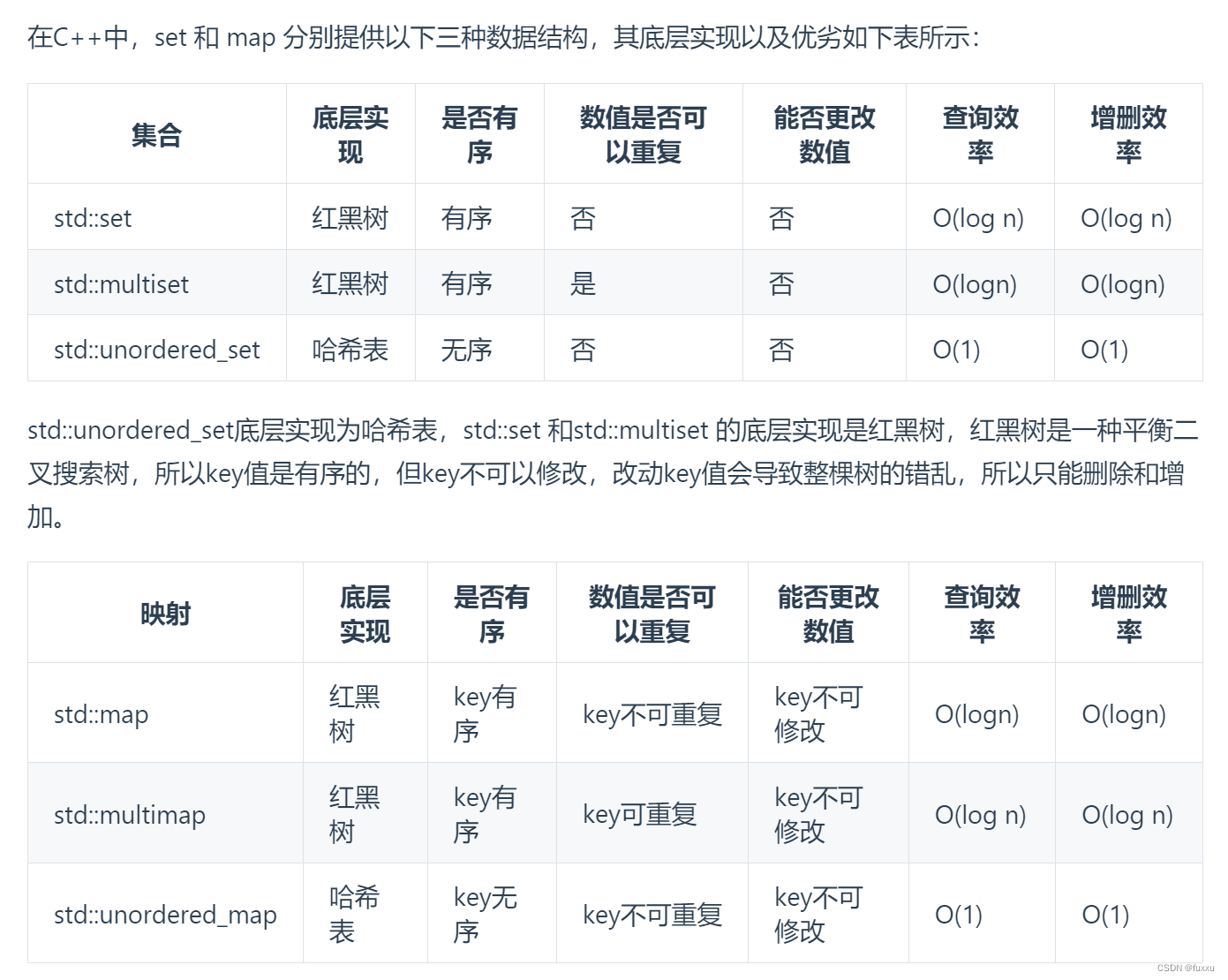
重新回忆一下下边这张表:(链接:代码随想录
代码
class Solution {
public:
bool halvesAreAlike(string s) {
set<char> vowels = {'a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'};
int counta = 0, countb = 0;
for (int i = 0; i < s.size() / 2; ++i) {
int j = i + s.size() / 2;
if (vowels.find(s[i]) != vowels.end()) {
counta++;
}
if (vowels.find(s[j]) != vowels.end()) {
countb++;
}
}
return counta == countb;
}
};时间复杂度
1. **初始化元音集合**: 这是一个常数时间操作,因为集合中的元素数量是固定的(10个元音字母)。
2. **遍历字符串**: 代码遍历了字符串 `s` 的每个字符一次。因此,这部分的时间复杂度与字符串的长度 `n` 线性相关,即 `O(n)`。
3. **查找集合中的元素**: 每次遍历时,代码都会检查当前字符是否为元音字母。在`set`中查找元素的时间复杂度是 `O(log m)`,其中 `m` 是集合中元素的数量。由于元音字母的数量是固定的(10个),这可以近似视为常数时间操作,即 `O(1)`。
综上所述,总的时间复杂度主要由字符串的遍历决定,即为 `O(n)`。
空间复杂度
1. **元音集合**: 这个集合包含了10个元音字母,是一个常数空间占用,即 `O(1)`。
2. **计数器**: 使用了两个整型变量 `count1` 和 `count2` 来计数,这也是常数空间占用。
因此,总的空间复杂度为 `O(1)`,也就是说,空间复杂度是常数级的。
综上,这段代码的时间复杂度是 `O(n)`,空间复杂度是 `O(1)`。
文章来源:https://blog.csdn.net/fuxxu/article/details/135570185
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!