信号处理基础之噪声与降噪(一) | 噪声分类及python代码实现

后续将给大家分享信号处理基础系列文章，本期是讲噪声相关知识，包括噪声的定义、分类及python代码实现。

1. 噪声的定义

噪声是信息信号在传输过程中所受到的各种各样干扰信号的总成，其直接影响信号的传输质量，甚至破坏正常的信号。通俗地，噪声定义为信号中的无用信号成分，噪声信号混杂在原始信号中，引起信号的失真。

噪声也可以指包含很多频率的信号，即信号的频谱呈现随机性。噪声无处不在，在一些场合，噪声可以被利用，进而分析和观察系统的输出特性。

为了排除噪声的影响，DSP最重要的应用之一是消除信号中的噪声。

2. 噪声的分类

按照噪声对信号的干扰形式分：可分为加性噪声和乘性噪声。

• 加性噪声：噪声和信道内传输的信号之间存在着相互叠加的关系，其特点是噪声是独立存在的，与信道信号的有无无关，其对信号传输质量影响较大。加性噪声在实际应用中只能被设法减小，无法被彻底清除。
• 乘性噪声：噪声和信道内传输的信号之间存在相乘的关系，随着信号的存在而存在，当信号消失后，乘性噪声也将湮没。

按照噪声的功率谱分：可分为白噪声和有色噪声。

• 白噪声：功率谱密度在整个频域内是常数的噪声。所有频率具有相同能量密度的随机噪声称为白噪声。若噪声的概率密度函数同时服从高斯分布，则称为高斯白噪声。具体地，白噪声定义如下：
  

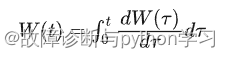
其功率谱密度可表示为：

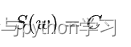
• 有色噪声：功率谱密度函数不平坦的噪声，有色噪声包括红噪声、粉噪声和蓝噪声等。
  红噪声：红噪声也成为布朗噪声，为随机移动噪声。红噪声的功率谱密度与其频率 成反比，即该类噪声在低频时有较大的能量。根据“布朗运动瞬时速度为零均值不相关白噪声”的布朗运动规律，布朗运动是对白噪声进行积分而来，可以得到布朗噪声的功率谱密度为
  

• 粉噪声：粉噪声介于白噪声和红噪声之间，在很宽频率范围内用等比例频带宽度测量时，频谱连续而均匀的噪声。在给定频率范围内（不含直流成分），随着频率的增加，其功率密度每倍频程下降3dB（密度与频率成反比）。
  粉噪声的功率谱密度可表示为：
  

• 蓝噪声：在有限频率范围内，功率密度随频率的增加每倍频增长3dB(密度正比于频率)。蓝噪声与粉噪声相对，与粉噪声正好相反，低频声音变得更弱，高频声音变得更强。一般地，将白噪声的低频部分加以抑制，高频部分增强，即可得到蓝噪声。
  紫噪声：在有限频率范围内，功率密度随频率的增加每倍频增长6dB(密度正比于频率的平方值)。其与红噪声相对，该类噪声在高频处有较大能量。

• 灰噪声：灰噪音是一种介于白噪音和粉红噪音之间的噪声类型，其频谱能量在不同频率上略有变化。
  黑噪声：黑噪音又称为静止噪音，它是一种具有危害性的噪音。它是在20000Hz以上的频率，一定程度上类似于超声波的噪音，这种黑噪音就像“黑光”一样，由于频率太高而使人们无法感知，但它对周围的环境仍然会构成影响，是一种有危害的噪音。黑噪声具有 ，在信号处理中，我们经常会提及狄拉克(Dirac)函数或单位脉冲，这种脉冲是指具有零宽度和无限高电平的信号。

总体而言，噪声是一个随机过程，而随机过程有其功率谱密度，功率谱密度函数的形状决定了噪声的“颜色”。

3. 基于python的噪声构造

白噪声

import numpy as np
from scipy import fftpack
import matplotlib.pyplot as plt
import matplotlib
# 生成白噪声

n_sampling = 10000
fs = 1000
white_noise = np.random.normal(0,5,n_sampling)
t = np.linspace(0, n_sampling / fs, n_sampling)
# 计算功率谱
p = fftpack.fft(white_noise)
power = np.abs(p)**2              # 计算功率谱 (幅度的平方)
power_db = 10 * np.log10(power)   # 幅值转换为分贝
f = np.fft.fftfreq(p.size, 1/fs)  # 计算频率

fig = plt.figure(figsize=(10, 6), dpi=100)
font = {'family': 'Times New Roman', 'size': 14, 'weight': 'normal',}
matplotlib.rc('font', **font)
grid = plt.GridSpec(8, 8, hspace=0.1)
plt.subplot(grid[0:2, 0:8])
plt.plot(t, white_noise, 'b')
plt.xlabel('time(s)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Amplitude', fontname='Times New Roman', fontsize=14)
plt.subplot(grid[3:8, 0:8])
plt.plot(f[0:n_sampling//2], power_db[0:n_sampling//2], 'r')
plt.xlabel('Frequency(Hz)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Magnitude(dB)', fontname='Times New Roman', fontsize=14)
plt.show()
fig.align_labels()

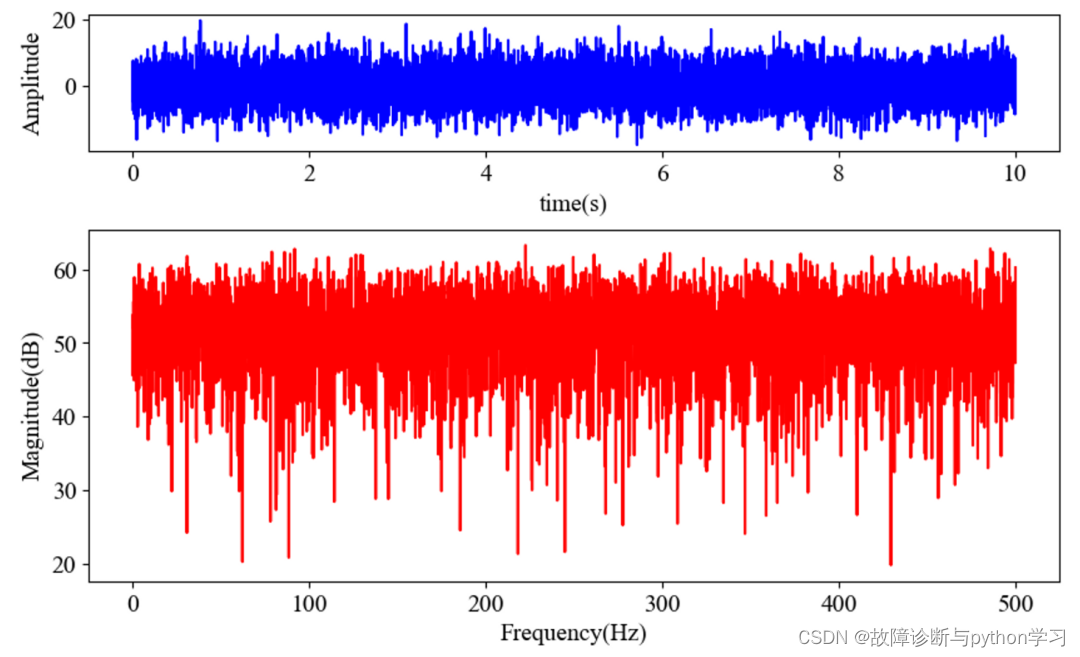
图1 白噪声及其功率谱

红噪声

import numpy as np
from scipy import fftpack
import matplotlib.pyplot as plt
import matplotlib

# 生成红噪声
n_sampling = 10000
fs = 1000
std = 3
white_noise = np.random.normal(0,5,n_sampling)
red_noise = np.cumsum(white_noise)
red_noise = red_noise / np.max(np.abs(red_noise)) * std
t = np.linspace(0, n_sampling / fs, n_sampling)
# 计算功率谱
p = fftpack.fft(red_noise)
power = np.abs(p)**2              # 计算功率谱 (幅度的平方)
power_db = 10 * np.log10(power)   # 幅值转换为分贝
f = np.fft.fftfreq(p.size, 1/fs)  # 计算频率

fig = plt.figure(figsize=(10, 6), dpi=100)
font = {'family': 'Times New Roman', 'size': 14, 'weight': 'normal',}
matplotlib.rc('font', **font)
grid = plt.GridSpec(8, 8, hspace=0.1)
plt.subplot(grid[0:2, 0:8])
plt.plot(t, red_noise, 'b')
plt.xlabel('time(s)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Amplitude', fontname='Times New Roman', fontsize=14)
plt.subplot(grid[3:8, 0:8])
plt.plot(f[0:n_sampling//2], power_db[0:n_sampling//2], 'r')
plt.xlabel('Frequency(Hz)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Magnitude(dB)', fontname='Times New Roman', fontsize=14)
plt.show()
fig.align_labels()

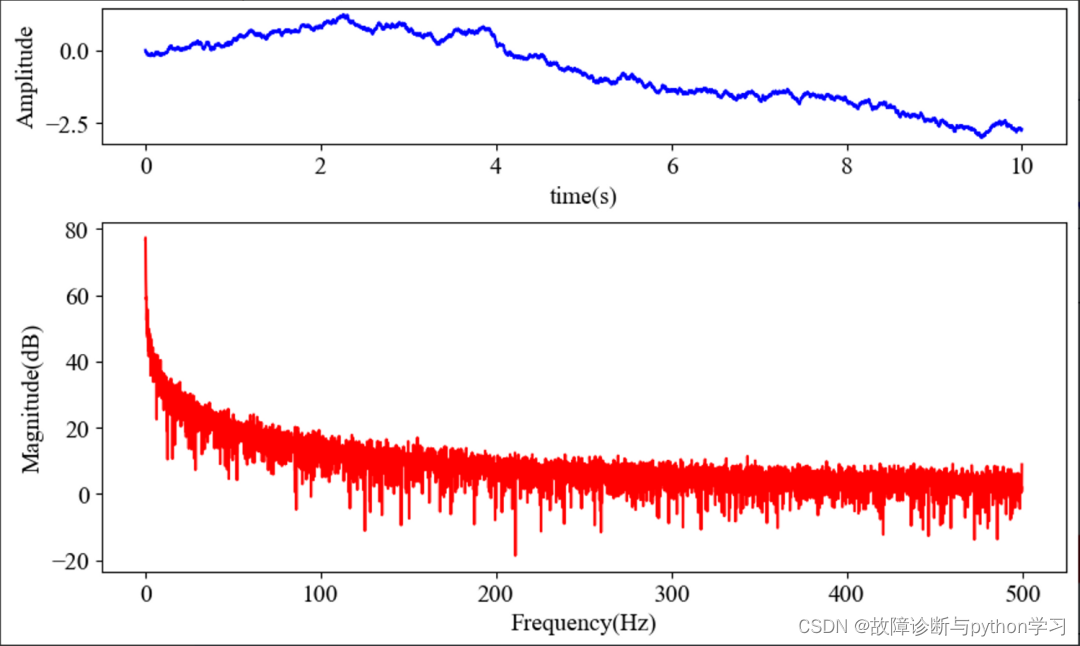
图2 红噪声及其功率谱
蓝噪声

import numpy as np
from scipy import fftpack, signal
import matplotlib.pyplot as plt
import matplotlib
# 生成蓝噪声
n_sampling = 10000
fs = 1000
exponent = -1.5
white_noise = np.random.normal(0,5,n_sampling)
b, a = signal.butter(1, 0.5, 'high')
blue_noise = signal.lfilter(b, a, white_noise)
t = np.linspace(0, n_sampling / fs, n_sampling)
# 计算功率谱
p = fftpack.fft(blue_noise)
power = np.abs(p)**2              # 计算功率谱 (幅度的平方)
power_db = 10 * np.log10(power)   # 幅值转换为分贝
f = np.fft.fftfreq(p.size, 1/fs)  # 计算频率

fig = plt.figure(figsize=(10, 6), dpi=100)
font = {'family': 'Times New Roman', 'size': 14, 'weight': 'normal',}
matplotlib.rc('font', **font)
grid = plt.GridSpec(8, 8, hspace=0.1)
plt.subplot(grid[0:2, 0:8])
plt.plot(t, blue_noise, 'b')
plt.xlabel('time(s)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Amplitude', fontname='Times New Roman', fontsize=14)
plt.subplot(grid[3:8, 0:8])
plt.plot(f[0:n_sampling//2], power_db[0:n_sampling//2], 'r')
plt.xlabel('Frequency(Hz)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Magnitude(dB)', fontname='Times New Roman', fontsize=14)
plt.show()
fig.align_labels()

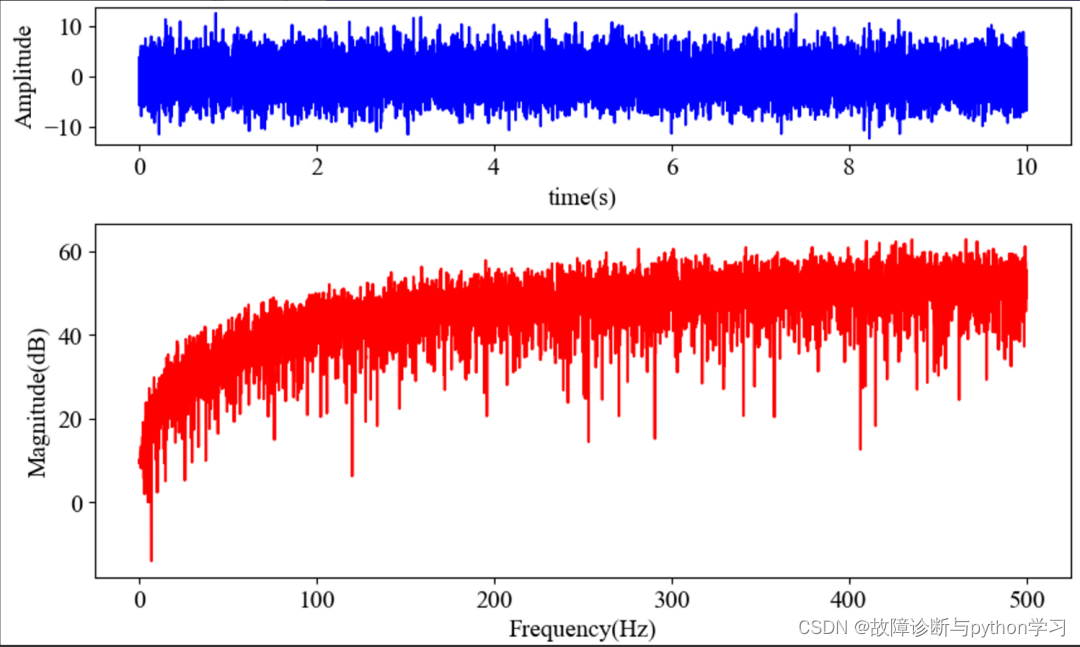
图3 蓝噪声及其功率谱
紫噪声

import numpy as np
from scipy import fftpack
import matplotlib.pyplot as plt
import matplotlib
# 生成紫噪声
n_sampling = 10000
fs = 1000
white_noise = np.random.normal(0,5,n_sampling)
purple_noise = np.diff(white_noise, 2)
t = np.linspace(0, len(purple_noise) / fs, len(purple_noise))
# 计算功率谱
```python
p = fftpack.fft(purple_noise)
power = np.abs(p)**2              # 计算功率谱 (幅度的平方)
power_db = 10 * np.log10(power)   # 幅值转换为分贝
f = np.fft.fftfreq(p.size, 1/fs)  # 计算频率
fig = plt.figure(figsize=(10, 6), dpi=100)
font = {'family': 'Times New Roman', 'size': 14, 'weight': 'normal',}
matplotlib.rc('font', **font)
grid = plt.GridSpec(8, 8, hspace=0.1)
plt.subplot(grid[0:2, 0:8])
plt.plot(t, purple_noise, 'b')
plt.xlabel('time(s)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Amplitude', fontname='Times New Roman', fontsize=14)
plt.subplot(grid[3:8, 0:8])
plt.plot(f[0:len(purple_noise)//2], power_db[0:len(purple_noise)//2], 'r')
plt.xlabel('Frequency(Hz)', fontname='Times New Roman', fontsize=14)
plt.ylabel('Magnitude(dB)', fontname='Times New Roman', fontsize=14)
plt.show()
fig.align_labels()

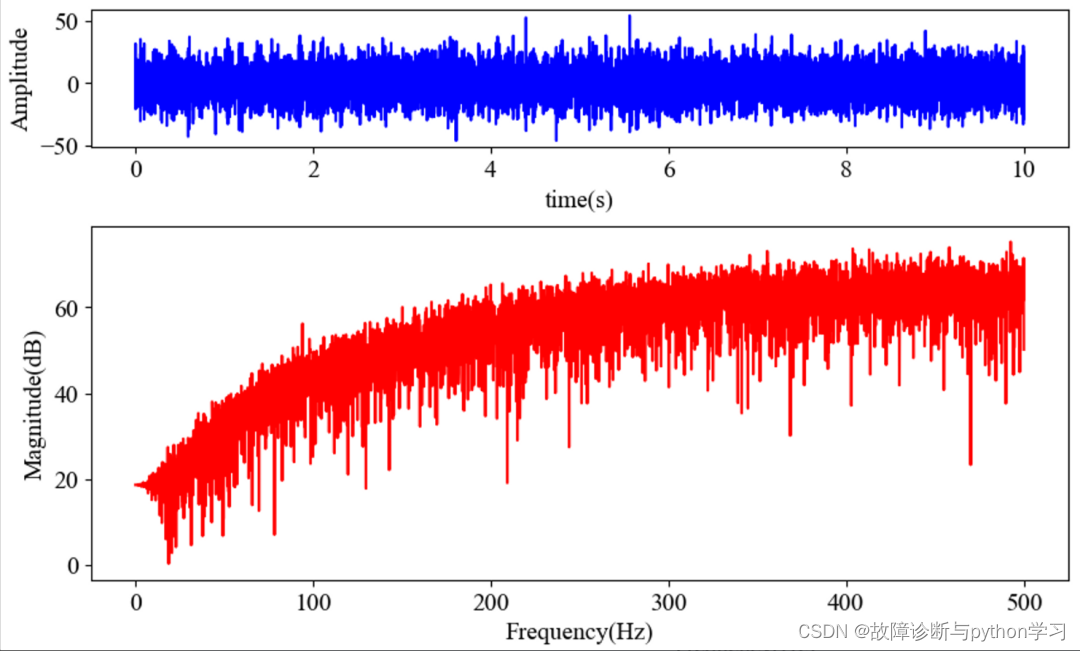
图4 紫噪声及其功率谱
粉噪声/黑噪声

import numpy as np
def generate_pink_or_black_noise(samples, sample_rate, alpha):
"""
这里的alpha参数决定了噪声的颜色。alpha=1.0对应于粉噪声。如果你想生成其他颜色的噪声，
可以改变这个参数。例如，alpha=1.5将生成黑噪声，alpha=0.0将生成白噪声。
"""
    omega = np.fft.fftfreq(samples, d=1./sample_rate)
    s_scale = omega
    s_scale[0] = 1
    sr = np.random.normal(scale=np.sqrt(np.abs(s_scale)**-alpha))
    si = np.random.normal(scale=np.sqrt(np.abs(s_scale)**-alpha))
    s = sr + 1j*si
    y = np.fft.ifft(s).real
    return y

使用函数生成粉噪声

pink_noise = generate_pink_or_black_noise(10000, sample_rate, alpha)

关注公众号《故障诊断与python学习》，了解更多故障诊断干货
往期推荐

[1] 故障诊断代码实战之第1期 | 手把手教你安装python环境(Anaconda)及跑通第一个信号处理案例！！！

[2] 机械故障诊断信号的幅域分析 - 时域统计特征 | 基于python的代码实现，在CWRU和IMF轴承数据集上实战

[3] 机械故障诊断信号的幅域分析 - 幅值概率密度函数 | 基于python的代码实现，在CWRU轴承数据上实战

[4] Python学习｜第1篇，用python读取CWRU数据集