python算法问题,求两个字符串的最长公共子序列长度
发布时间:2024年01月03日
对于问题,两个字符串的最长公共子序列长度进行求解,首先要知道子序列的定义,如果说给定一个字符串,对这个字符串中的原有字符进行不改变字符相对位置的删除,这里的相对位置就是处于前还是后的相对关系,进行删除字符的操作之后,所形成的新的字符串就是原来的字符串的子序列。
这里要求解的问题,就是给定两个字符串S1和S2,对这两个字符串进行子序列的比对,得到一个共同的子序列,求这个子序列的最长字符长度。如下例子:

添加图片注释,不超过 140 字(可选)
对于以上问题,如果说不使用动态规划等思路的求解,暴力求解所产生的计算量非常大,造成时间复杂度很高的后果,所以选择使用动态规划思路求解,并且使用二维动态规划,这里主要借助于一个二维数组来进行模拟。
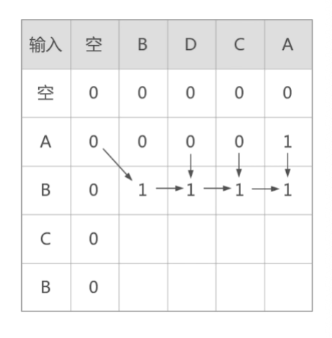
使用一个L(i,j),这里代表的是S1字符串的前m位中的前i个字符和S2字符串的前n位的前j个字符的最长公共子序列的长度,对于该问题的状态转移方程分为3种情况,分别是,当m和n都是0的时候,则有L(m,n)=0,第二种情况是当m和n都大于0的时候,并且对应的S1的m位字符和S2的n位字符相同时,L(m,n)=L(m-1,n-1)+1,第三种情况是当m和n都大于0的时候,并且对应的S1的m位字符和S2的n位字符不相同时,L(m,n)=max(L(m,n-1),L(m-1,n))。下图为"ABCD"和"BDCA"字符串的判定最长公共子序列的长度的过程:
添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
python代码实现如下:
def longestequence(self, s1, s2):
len1=len(s1)
len2=len(s2)
array=[[0]*(len2+1) for _ in range(len1+1)]
for i in range(1,len1+1):
for j in range(1,len2+1):
if s1[i-1]==s2[j-1]:
array[i][j]=array[i-1][j-1]+1
else:
array[i][j]=max(array[i][j-1],array[i-1][j])
return array[len1][len2]
文章来源:https://blog.csdn.net/Mrsawyer/article/details/135361082
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 燃油车智能化时代将终结,长安汽车凭啥引领“数智新汽车”周期?
- Windows Server C盘空间不足怎么办?
- Mnajora 使用虚拟机安装windows server 2022 中的网络问题
- uniapp中组件库的Checkbox 复选框的使用方法
- element plus: el-upload详解
- Python:Jupyter
- java中的多态
- IDEA中显示方法、类注释信息
- 批量AI智剪技巧:学会视频剪辑,让视频更具吸引力的方法
- Linux版本下载Centos操作