区间dp模型整理

区间dp的核心就是我们需要对一段区间或者是可以抽象成区间的范围进行划分，不同的划分有不同的结果，我们要找的就是最佳划分。其实一般划分这里都不是很容易看出来，所以我们可以先从比较小的例子来看看看是否涉及从区间中进行选择的问题，一旦涉及在区间中选择，那么就可以用区间dp。

282. 石子合并（活动 - AcWing）

思路：我们来看这里现在有n堆石子，只有相邻两堆可以合并，代价为两堆的石子个数和。问将所有的都合并的最小花费。这题如果不要求顺序的话，可以用贪心来写，每次挑出最小的两堆合并，但是这里要求顺序，我们按照堆数从小到大枚举

一堆：那么就不变

两堆直接合并,代价a+b

三堆a,b,c就要考虑先合并哪两堆

四堆也要考虑先合并哪两堆

我们可以划分成不同的区间，被合并的两个被分进一个区间当中。

比如三堆我们可以如下来分：
[a,a],[b,c]

[a,b],[c,c]

所以区别就是从哪里开始划分区间。

我们可以按照这个来分。?

状态表示：定义dp[l][r]为合并区间[l,r]的花费，属性为最小值

?状态划分：可以按照区间从哪里分成两部分来进行划分。

如果从位置k开始划分，那么dp[l][r]=dp[l][k]+dp[k+1][r]+sum(l,r);

那么我们还要考虑一下循环怎么写，显然如果第一维循环l,第二维循环r，第三维循环k(划分位置)的话，我们会在循环的时候用到一些还没有计算过的数。

那么这里我们换一种方法来进行循环，我们第一维循环区间长度，第二维循环左端点位置，由此可以算出右端点位置，然后第三维循环划分位置k，这样的话，我们划分用到的一定是更短的区间，更短的区间我们之前算过，就不会出问题。

然后至于初值位置，我们只要在开始考虑这个区间前，把它设置成负无穷即可。

#include<bits/stdc++.h>
using namespace std;
int a[400],dp[400][400];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i]+=a[i-1];
    for(int len=2;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int l=i,r=i+len-1;
            dp[l][r]=1e8;
            for(int k=l;k<r;k++)
            {
                dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]+a[r]-a[l-1]);
            }
        }
    }
    cout<<dp[1][n];
}

1068. 环形石子合并(活动 - AcWing)

思路：很显然这里也是要将一排合成一堆，但是每次只能合并两堆的问题，但是这里有一点不同，这里的石子是环形的，也就是首尾相接。?这里实际上可以将环拆成链，那么拆出来的链显然少了一些顺序，如何获得这些顺序呢，我们可以将拆出来的链复制一下补在后面，那么环中可以得到的所有区间，我们现在都可以得到了。最后计算结果的时候，我们只需要看从每个点开始，n长的区间的花费是多少，找一个最小值即可。本质上，我们可以从任意一个地方展成一条链，展成的这些链，开头和结尾的区间不同，这也它们之间的区别，那么实际上我们只要将不同开头和结尾的定长区间都处理出来即可。

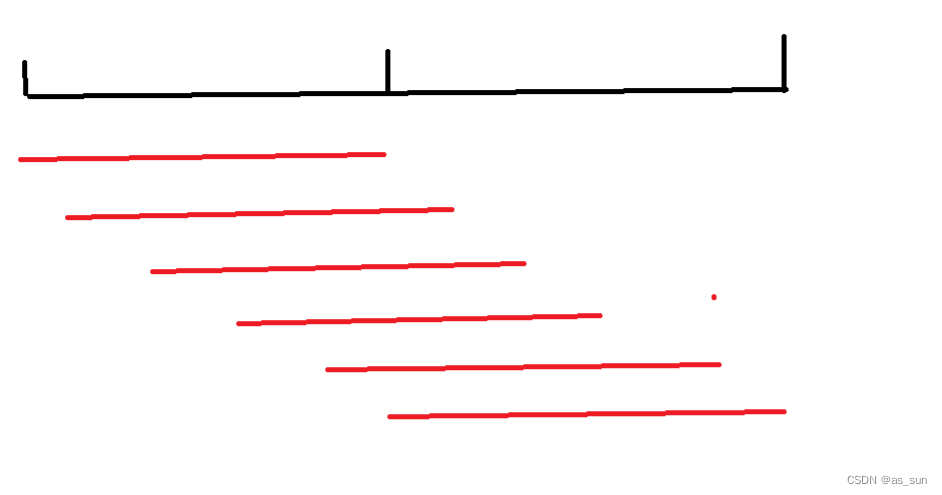
?然后最大最小值分计算即可

#include<bits/stdc++.h>
using namespace std;
int a[600],s[600],dp[600][600],dp1[600][600];
int main()
{
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i+n]=a[i];
        for(int i=1;i<=2*n;i++) s[i]=s[i-1]+a[i];
        for(int len=2;len<=n;len++)
        {
            for(int i=1;i+len-1<=n*2;i++)
            {
                int l=i,r=i+len-1;
                dp[l][r]=1e8,dp1[l][r]=-1e8; 
                for(int k=l;k<r;k++)
                {
                    dp1[l][r]=max(dp1[l][r],dp1[l][k]+dp1[k+1][r]+s[r]-s[l-1]);
                    dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]+s[r]-s[l-1]);
                }
            }
        }
        int mi=0x3f3f3f3f,mx=-0x3f3f3f3f;
        for(int i=1;i<=n;i++) 
        {
            mx=max(mx,dp1[i][i+n-1]);
            mi=min(mi,dp[i][i+n-1]);
        }
        cout<<mi<<endl<<mx<<endl;
 
}

320. 能量项链（活动 - AcWing）

?

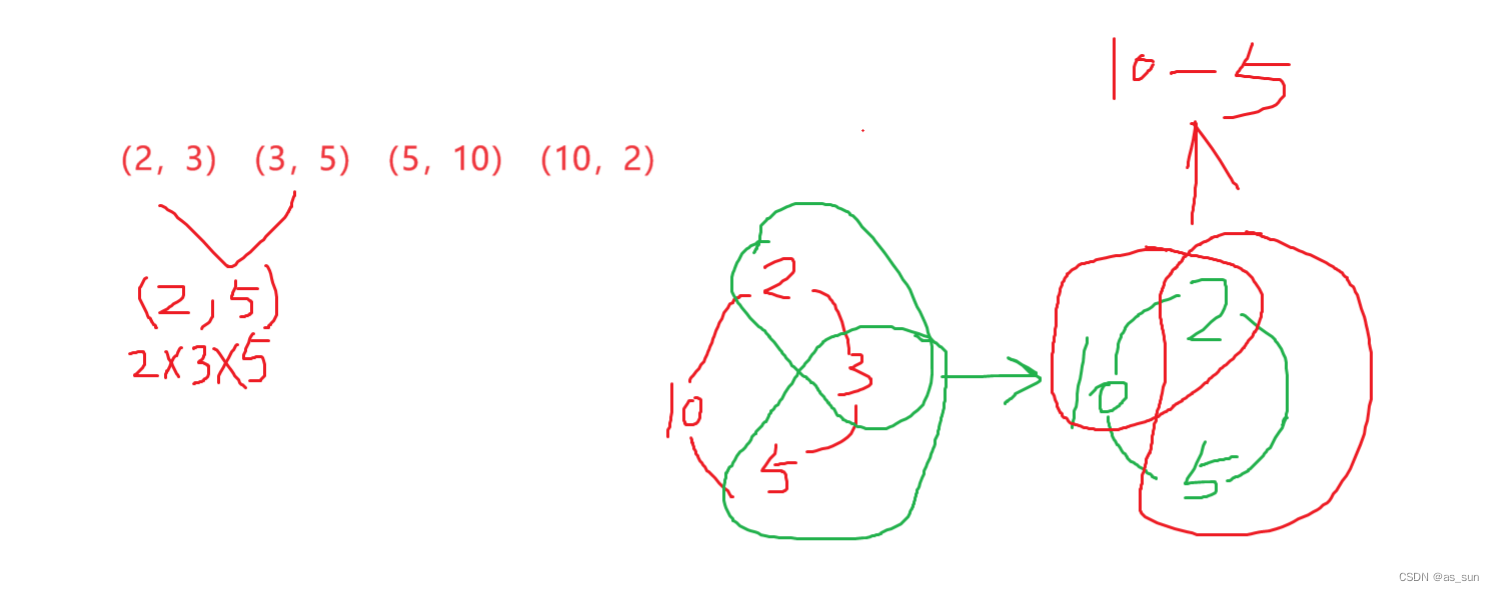
差不多就是这个意思，当然对于这个圈，只要相邻的三个就可以操作，因为给的这些头尾相交，任意两个点一定属于某个石头。这里既然出现环，我们当然也可以像上道题一样展成链。

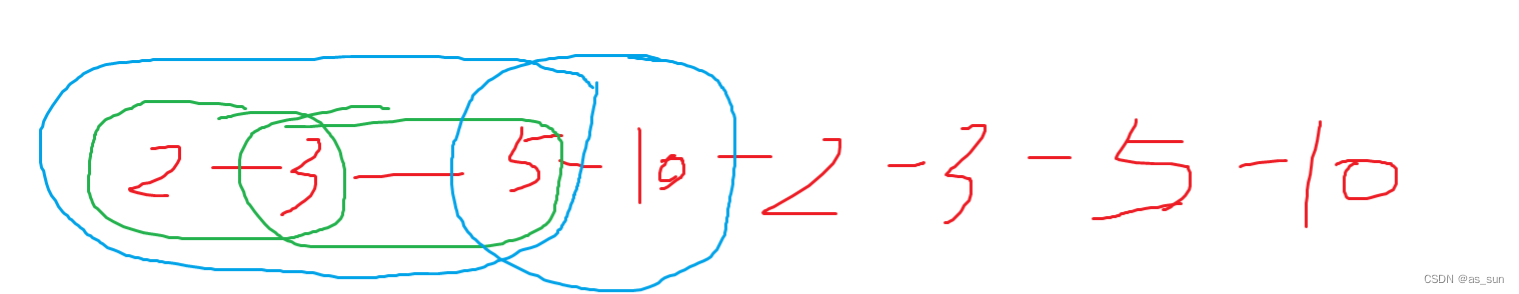?尽管和上面稍有不同，但是也是一种合法方案。我们据此来看[2,10]实际划分成了[2,5],[5,10]，能量是2*5*10,[2,5]划分成了[2,3],[3,5]，花费是2*3*5，那么推广开来：dp[l][r]=dp[l][k]+dp[k][r]+l*k*r.

另外还要注意一下，上个题可以合并的区间最少两个点，但这个题可以合并的区间最少三个点，所以len要从3开始。

#include<bits/stdc++.h>
using namespace std;
int a[300],dp[300][300];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i+n]=a[i];
    for(int len=3;len<=n+1;len++)//
    {
        for(int i=1;i+len-1<=2*n;i++)
        {
            int l=i,r=l+len-1;
            dp[l][r]=-1e18;
            for(int k=l+1;k<r;k++)
            {
                dp[l][r]=max(dp[l][r],dp[l][k]+dp[k][r]+a[l]*a[k]*a[r]);
                //printf("%d %d %d %d\n",l,k,r,dp[l][r]);
            }
        }
    }
    int mx=0;
    for(int i=1;i<=n;i++)
    {
        mx=max(mx,dp[i][i+n]);
    }
    cout<<mx;
}

?479. 加分二叉树（活动 - AcWing）

思路：由二叉树的定义我们很容易知道，前序遍历和中序遍历可以唯一确定一棵二叉树，但是仅仅只有中序遍历，那么可以得到的二叉树有很多种。?因为根节点可以在任意位置，那么如果我们确定了根节点的位置，那么根节点左右就只能一半属于左子树，一半属于右子树。这就很像区间dp问题中找一个分界点。这里最小的一段区间显然也是三个点，那么我们可以类比能量项链来写。

但是它与能量项链还是不同的，首先在一段区间内，左右端点是有可能为根节点的，其次我们这里讨论的区间长度为1，为2都是可以的；同时还要注意到根节点取到左右端点的时候的左右根的值要特殊处理一下；最后那个前序遍历就意味着我们要记录每个区间的根节点，最后dfs来写即可。

#include<bits/stdc++.h>
using namespace std;
int a[40],s[40],dp[40][40],g[40][40];
void dfs(int l,int r)
{
    if(l>r) return;
    int t=g[l][r];
    cout<<t<<" ";
    dfs(l,t-1);
    dfs(t+1,r);
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) s[i] = a[i]+s[i-1];

    for(int len=1;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)//并非环
        {
            int l=i,r=i+len-1;
            if(len==1) dp[l][r]=a[i],g[l][r]=l;
            else
            {
                dp[l][r]=-1e8;
                for(int k=l;k<=r;k++)
                {
                    int left=k==l?1:dp[l][k-1];
                    int right=k==r?1:dp[k+1][r];
                    int score=left*right+a[k];
                    if(dp[l][r]<score)
                    {
                        dp[l][r]=score;
                        g[l][r]=k;
                    }
                }
            }
        }
    }
    cout<<dp[1][n]<<endl;
    dfs(1,n);
}

1069. 凸多边形的划分（活动 - AcWing）

我们以样例来分析：?

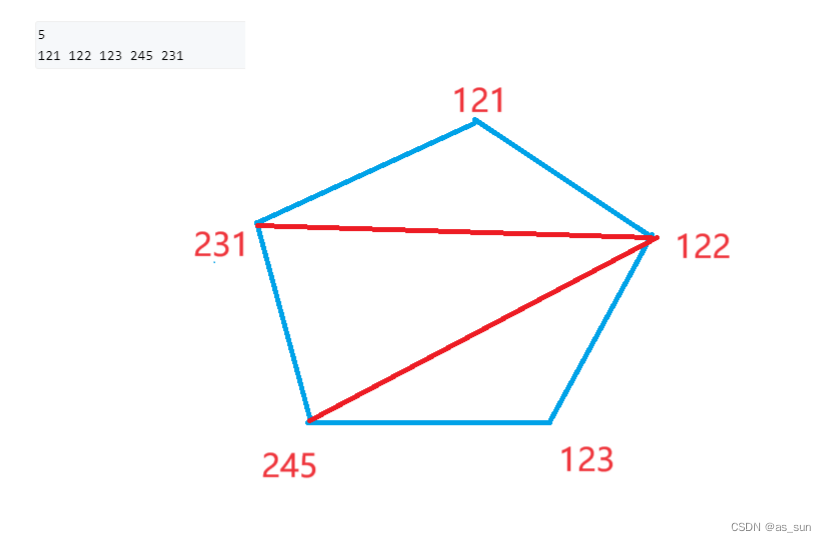
显然我们以一条边作为底构成三角形后，剩余的点就被分到左右两边去了，由于三角形不能交叉，那么左右的点肯定各自组成三角形。

那么我们确定两点之后，剩下的这个点怎么选，肯定是在这两点之间，由于是一个环，所以我们实际上可以如上面一样展成链来写。这里也是，区间长度至少为3。不过我们再想一想，上面展成环的时候，是因为有一条边有空缺，但很明显这里的每一条边都会被用上，所以不展成环其实也可以。

这题最关键的地方在于，数据范围比较大，而且没有说在int范围内，甚至我们注意到，如果三个1e9相乘，是会爆long long的。所以要用到高精度乘法和高精度加法。

#include<bits/stdc++.h>
using namespace std;
const int N=55,M=35;
typedef long long ll;
int w[N];
ll dp[N][N][M];
void mul(ll a[],ll b)
{
    ll c[M];
     memset(c,0,sizeof c);
    ll t=0;
    for(int i=0;i<M;i++)
    {
        t += a[i]*b;
        c[i]=t%10;
        t /= 10;
    }
    memcpy(a,c,sizeof c);
}
void add(ll a[],ll b[])
{
    ll c[M];
    memset(c,0,sizeof c);
    for(int i=0,t=0;i<M;i++)
    {
        t += (a[i]+b[i]);
        c[i]=t%10;
        t /= 10;
    }
    memcpy(a,c,sizeof c);
}
int cmp(ll a[],ll b[])
{
    for(int i=M-1;i>=0;i--)
    {
        if(a[i]>b[i]) return 1;
        else if(a[i]<b[i]) return -1;
    }
    return 0;
}
void print(ll a[])
{
    int k=M-1;
    while(k&&!a[k]) k--;
    while(k>=0)cout<<a[k--];
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    ll tmp[M];
    for(int len=3;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int l=i,r=i+len-1;
            dp[l][r][M-1]=1;
            for(int k=l+1;k<r;k++)
            {
                memset(tmp,0,sizeof tmp);
                tmp[0]=w[l];
                mul(tmp,w[k]);
                mul(tmp,w[r]);
                add(tmp,dp[l][k]);
                add(tmp,dp[k][r]);
                if(cmp(dp[l][r],tmp)>0) memcpy(dp[l][r],tmp,sizeof tmp);
            }
        }
    }
    print(dp[1][n]);
}

?321. 棋盘分割(321. 棋盘分割 - AcWing题库)

?

我们来看一下题目，就是将棋盘拆成两块，其中一块不动，将剩下一块儿继续这么分。分n-1次，得到n块。然后求上式的值。我们可以将这个式子化简一下：

?

所以我们只要把每一块儿内的平方求出来即可，因为平均数是固定的。要求每一块儿的平方，首先得求出每一块儿的值，这里可以用二维前缀和来实现。

结果的结算部分解决了之后就是来看，我们每一块儿是什么，也即如何划分。

?

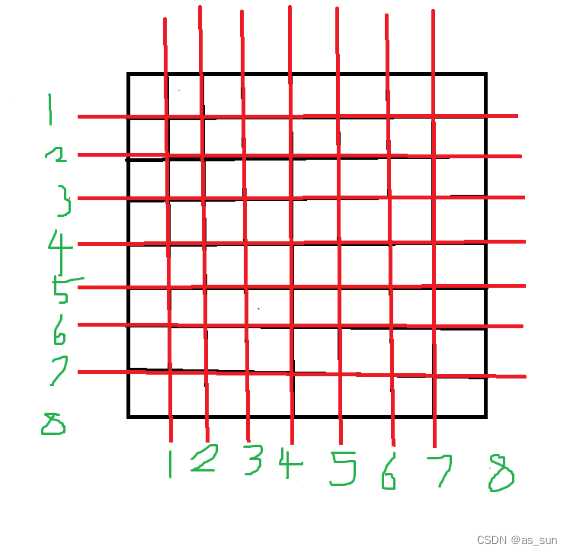
ps：因为数在格子中，所以为了方便统一线和格子，我们如图进行标号?

如图，我们第一刀横着切有七个位置，纵着切也有七个位置，然后切完之后得到的两部分也有两种选法。但是我们注意每一刀都在一个范围之内，那么就是从这个范围内选位置，就与区间dp联系上了。?显然我们要考虑的情况太多了，所以这里采用记忆化搜索的方式。所以dp部分的处理如下：

int dp(int x1,int y1,int x2,int y2,int k)//（x1,y1）是左上角的坐标，(x2,y2)是右下角的坐标，k表示切了多少刀了
{
    double &v=f[x1][y1][x2][y2][k];
    if(v>=0) return v;//如果已经有值，那么直接返回，有点像剪枝，搜过一次就不再往后搜了
    if(k==1) return v=get(x1,y1,x2,y2);//最多只能切7刀，我们传入的初值是8，所以为1的时候退出
    v=INF;
    for(int i=x1,i<x2;i++)
    {
        v=min(v,get(x1,y1,i,y2)+dp(i+1,y1,x2,y2,k-1));//切下边
        v=min(v,get(i+1,y1,x2,y2)+dp(x1,y1,i,y2,k-1));//切上边
    }
    for(int i=y1;i<y2;i++)
    {
        v=min(v,get(x1,y1,x2,i)+dp(x1,i+1,x2,y2,k-1));//切左边
        v=min(v,get(x1,i+1,x2,y2)+dp(x1,y1,x2,i,k-1));//切右边
    }
    return v;
}

然后将二维前缀和和dp结合一下：

#include<bits/stdc++.h>
using namespace std;
const int N=10,M=20;
double f[N][N][N][N][M];
double a[N][N],s[N][N];
int n;
const double INF=1e9;
double get(int x1,int y1,int x2,int y2)
{
    double t=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
    return t*t;
}
double dp(int x1,int y1,int x2,int y2,int k)//（x1,y1）是左上角的坐标，(x2,y2)是右下角的坐标，k表示切了多少刀了
{
    double &v=f[x1][y1][x2][y2][k];
    if(v>=0) return v;//如果已经有值，那么直接返回，有点像剪枝，搜过一次就不再往后搜了
    if(k==1) return v=get(x1,y1,x2,y2);//最多只能切7刀，我们传入的初值是8，所以为1的时候退出
    v=INF;
    for(int i=x1;i<x2;i++)
    {
        v=min(v,get(x1,y1,i,y2)+dp(i+1,y1,x2,y2,k-1));//切下边
        v=min(v,get(i+1,y1,x2,y2)+dp(x1,y1,i,y2,k-1));//切上边
    }
    for(int i=y1;i<y2;i++)
    {
        v=min(v,get(x1,y1,x2,i)+dp(x1,i+1,x2,y2,k-1));//切左边
        v=min(v,get(x1,i+1,x2,y2)+dp(x1,y1,x2,i,k-1));//切右边
    }
    return v;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++) 
            scanf("%lf",&a[i][j]);
    for(int i=1;i<=8;i++)
    {
        for(int j=1;j<=8;j++)        
        {
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
        }
    }
    double x=(double)s[8][8]/n;
    memset(f,-1,sizeof f);//这里实际上是把f赋成NAN，就根本不是一个数
    dp(1,1,8,8,n);
    double ans=f[1][1][8][8][n];
    ans /= n;
    ans -= x*x;
    printf("%.3lf",sqrt(ans));
}