卡尔曼滤波学习笔记

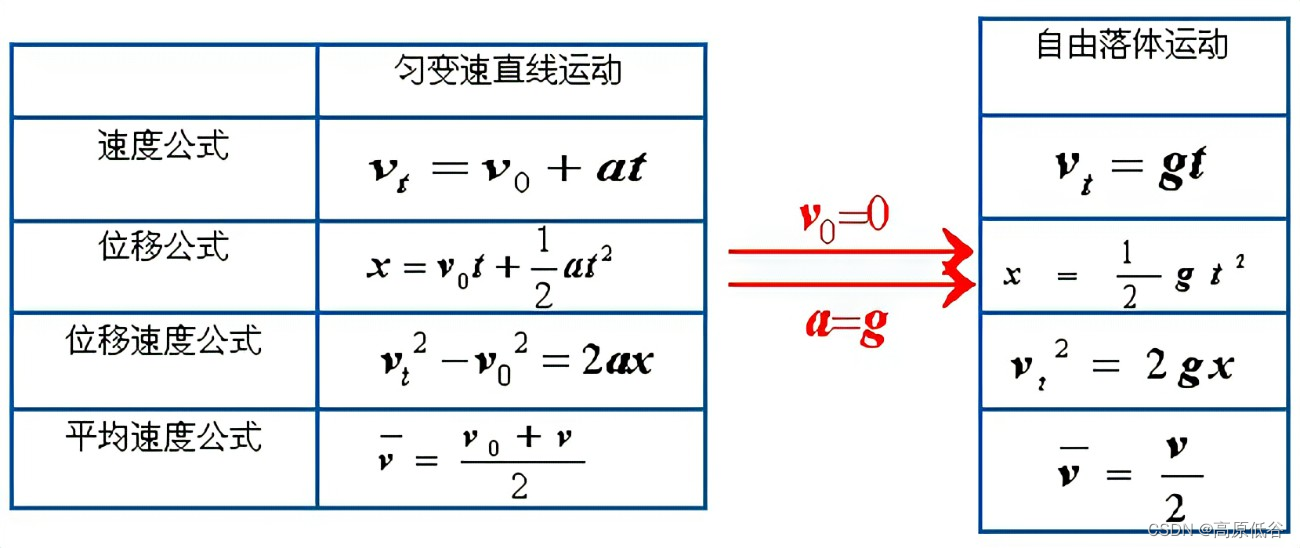
1卡尔曼滤波原理

1.1状态转移??

个人对矩阵浅显的理解，规定了矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。再规定两个这种集合间可以进行加减乘除，最后规定矩阵（数学术语）_百度百科 (baidu.com)加减乘除是怎么个加减乘除。以此基础推演发散高出各种花样。

矩阵（数学术语）_百度百科 (baidu.com)

可以通过计算得到过段时间的状态，但是这是一种推测。

1.2协方差矩阵

协方差矩阵：按照长方阵列排列的协方差值，下图为协方差值的计算过程

所有推测都是包含噪声的，噪声越大，不确定性就越大。某次推测的不确定性的大小，可以用协方差矩阵来表示。即用多个协方差值描述推测的不确定性的大小。

下图公式二用于表示不确定性在各个时间的传递关系

1.3观察矩阵

1.4状态更新

下图公式推导比较复杂，这里只是定性的分析一下。

我们已经有了观测量Z和观测噪声的协方差矩阵R，那么如何把他们整合进，我们对状态X的估计呢？

卡尔曼系数K作用：

1）权衡预测状态协方差P和观测噪声的协方差矩阵R的大小后，决定是详细预测模型多一点呢？还是相信观察模型多一点？

2）把残差的表现形式，由观察域，转化到状态域。在我们这个行车的例子中，我们观察到了汽车的位置，但是K里面已经包含了协方程矩阵P的信息，所以就是在利用位置和速度两个量的相关性，从位置的残差里推出了速度的残差。实现对车的状态的位置和速度两个维度，进行同时修正。

1.5噪声协方差矩阵的更新