坚持刷题 | 二叉树的最大深度
发布时间:2024年01月22日
坚持刷题,老年痴呆追不上我,今天刷:二叉树的最大深度
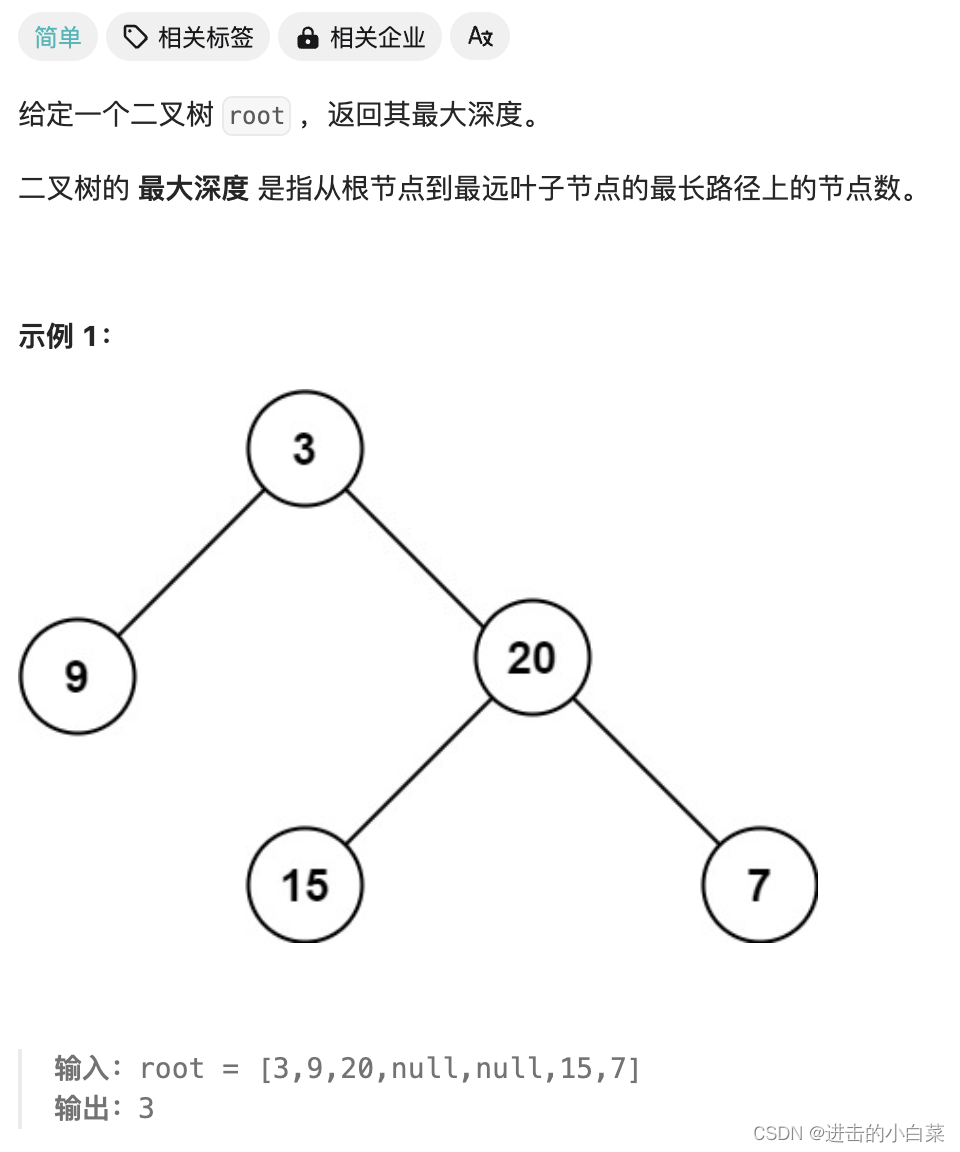
题目
考察点
- 二叉树的基本实现: 能够定义二叉树节点(TreeNode)以及构建一个二叉树的基本结构
- 递归的理解和运用: 能够使用递归的方式遍历二叉树节点
- 树的深度计算: 能够理解并实现计算二叉树深度的算法
代码实现
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeDepth {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
// 返回左右子树深度的较大值加上当前节点的深度(1)
return Math.max(leftDepth, rightDepth) + 1;
}
}
public static void main(String[] args) {
// 创建一个二叉树示例
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
BinaryTreeDepth binaryTreeDepth = new BinaryTreeDepth();
int depth = binaryTreeDepth.maxDepth(root);
System.out.println("二叉树的深度为:" + depth);
}
}
实现总结
- 递归的理解和使用:通过递归计算左右子树的深度,并在递归的基础上计算当前节点的深度
- 树的深度计算:通过比较左右子树的深度,选择较大值,并在此基础上加上当前节点的深度(1),得到整个二叉树的深度
- 时间复杂度: O(N),其中 N 是二叉树中的节点数。每个节点都会被访问一次,因此时间复杂度是线性的
- 空间复杂度: O(H),其中 H 是二叉树的高度。递归调用会使用系统调用栈,因此空间复杂度取决于递归的深度,即树的高度。在最坏的情况下,如果树是一个单链表形式的完全不平衡树,空间复杂度为 O(N);在最好的情况下,如果树是平衡二叉树,空间复杂度为 O(log N)
- 递归调用会占用栈空间,每次递归调用都会将当前状态保存在栈中,因此空间复杂度主要取决于递归的深度。在实际应用中,需要考虑递归深度是否可能达到系统栈的限制
扩展
用迭代的方式实现二叉树最大深度
import java.util.LinkedList;
import java.util.Queue;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeDepth {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
TreeNode current = queue.poll();
if (current.left != null) {
queue.offer(current.left);
}
if (current.right != null) {
queue.offer(current.right);
}
}
depth++;
}
return depth;
}
public static void main(String[] args) {
// 创建一个二叉树示例
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
BinaryTreeDepth binaryTreeDepth = new BinaryTreeDepth();
int depth = binaryTreeDepth.maxDepth(root);
System.out.println("二叉树的深度为:" + depth);
}
}
在该迭代的实现方式参考了 坚持刷题|二叉树的层序遍历,使用了队列来进行层序遍历,每遍历一层,深度加1。这样可以在不使用递归的情况下计算二叉树的深度。这种方法的时间复杂度同样是 O(N),其中 N 是二叉树中的节点数。
可能的扩展问题
- 如何使用非递归计算二叉树的深度,对应的时间和空间复杂度是多少?
- 能实现除深度计算外的其他二叉树遍历方式吗?能简要说明它们的应用场景吗?
- 了解其他二叉树操作吗?比如查找节点、插入和删除节点,可以提供简单的实现吗?
- 知道什么是平衡二叉树,为什么它很重要?能介绍一下 AVL 树或红黑树吗?
- 如何判断两颗二叉树是否相同?
- 在解决二叉树问题时,有没有方法可以优化空间复杂度,特别是不使用递归的情况下?
- 二叉树的深度优先搜索和广度优先搜索有什么区别?在什么情况下选择使用哪种方式?
文章来源:https://blog.csdn.net/weixin_44435110/article/details/135758702
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 配置测试MQtt
- C语言之scanf浅析
- 提升数据库性能的关键指南-Oracle AWR报告
- 3D渲染农场什么比较好用 2024渲染农场最新收费实测
- 揭示量化投资的神秘面纱:深入了解量化交易的核心原理!
- 微信如何群发消息?我来教你设置
- MinIO (五) .net core实现分片上传
- 《2023年度程序员收入报告》 :旧金山位居第一,北京程序员中位数超60万元
- APP定制开发合同
- Vue透传 Attributes的代码以及总结