leetcode(力扣) 89. 格雷编码 (规律题)
发布时间:2023年12月17日
题目描述
n 位格雷码序列 是一个由 2n 个整数组成的序列,其中:
每个整数都在范围 [0, 2n - 1] 内(含 0 和 2n - 1)
第一个整数是 0
一个整数在序列中出现 不超过一次
每对 相邻 整数的二进制表示 恰好一位不同 ,且
第一个 和 最后一个 整数的二进制表示 恰好一位不同
给你一个整数 n ,返回任一有效的 n 位格雷码序列 。
示例 1:
输入:n = 2
输出:[0,1,3,2]
解释:
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
00 和 01 有一位不同- 01 和 11 有一位不同
11 和 10 有一位不同- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列,其二进制表示是 [00,10,11,01] 。
00 和 10 有一位不同
10 和 11 有一位不同
11 和 01 有一位不同
01 和 00 有一位不同
思路分析
找规律题,
首先, 手写出来前几位的格雷编码。
当n = 0 和1时。
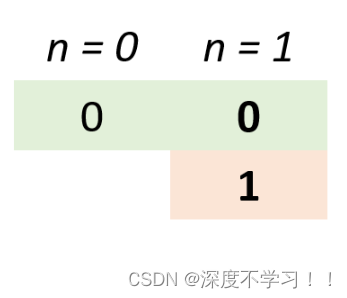
当n=2时候。
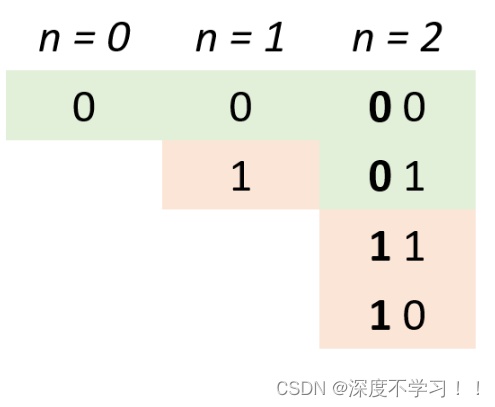
直接发现规律如下:
假设n = 1时的格雷编码为 g = [0,1] 则n=2时候的新格雷编码就由以下步骤得到:
- 每个元素二进制形式前面添加 0得到 new_g
- 将g颠倒过来,再将每一位前面加上1,得到 r
- 将new_g 和r 拼到一起 就是新的g。也就是n =3时候的g。
new_g = []
for i in g:
new_g.append('0'+str(i))
g = g[::-1]
r = []
for i in g:
r.append('1'+str(i))
g = new_g+r
最后将每一个字符串型二进制转换成整型十进制就行了。
完整代码
class Solution:
def grayCode(self, n: int) -> List[int]:
if n == 1:
return [0,1]
g = [0,1]
while n>1:
n -=1
new_g = []
for i in g:
new_g.append('0'+str(i))
g = g[::-1]
r = []
for i in g:
r.append('1'+str(i))
g = new_g+r
res = []
for i in g:
res.append(int(i,2))
return res```
文章来源:https://blog.csdn.net/qq_38737428/article/details/135034860
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 互联网加竞赛 python+深度学习+opencv实现植物识别算法系统
- 基于STM32F103的病房监控系统的设计
- 【js学习之路】遍历数组api之 `filter `和 `map`的区别
- k8s的陈述式资源管理
- centos安装jdk
- 安装DataEase(Linux线上安装)修改端口
- 《微信小程序开发从入门到实战》学习七十三
- Microsoft Visio 2021安装包如何下载和安装版本更新步骤2024
- 笔记——浏览器内核,底层机制
- 15 责任链模式