代码随想录算法训练营第三十八天|理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯

题目：理论基础

文章链接：代码随想录

?视频链接：动态规划理论基础

动态规划五部曲：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

?题目：509. 斐波那契数

文章链接：代码随想录

视频链接：LeetCode:509.斐波那契数

题目链接：力扣题目链接

图释：

class Solution {
public:
    // 确定dp数组（dp table）以及下标的含义 vector<int> dp, dp[i]表示第n哥斐波那契数 
    // 确定递推公式      dp[i]=dp[i-1]+dp[i-2]
    // dp数组如何初始化  dp[0]=1, dp[1]=1
    // 确定遍历顺序      从前往后
    // 举例推导dp数组    
    int fib(int n) {
        if(n<=0)return 0;
        if(n==1) return 1;
        vector<int> dp(n+1);
        dp[0]=0;
        dp[1]=1;
        for(int i=2; i<=n; i++){//从2开始，直到第n个数
             dp[i]= dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

class Solution {
public:
    int traversal(int n){
        // 终止条件
        if(n==1) return 1;
        if(n==0) return 0;

        // 递归
        return traversal(n-1)+traversal(n-2);
    }  
    int fib(int n) {  
        return traversal(n);
    }
};

再精简
class Solution {
public:
   int fib(int n) {  
        // 终止条件
        if(n==1) return 1;
        if(n==0) return 0;
        return fib(n-1)+fib(n-2);
    }
};

题目：70. 爬楼梯

文章链接：代码随想录

视频链接：LeetCode:70.爬楼梯

题目链接：力扣题目链接

图释：

class Solution {
public:
    // 确定dp数组（dp table）以及下标的含义 vector<int> dp, dp[i]表示达到第n层楼梯需要的方法 
    // 确定递推公式      dp[i]=dp[i-1]+dp[i-2]
    // dp数组如何初始化  dp[1]=1， dp[2]=2
    // 确定遍历顺序      从前往后
    // 举例推导dp数组  

    // 题目中要求的每次可以爬1或者2个台阶，也就是说，最终到达n阶台阶有两种方式，
    // 一个是爬1阶台阶到达（对应的是从n-1阶台阶开始）
    // 另一个就是爬2阶台阶到达（对应的是从n-2阶台阶开始爬），
    // 而爬n-1阶和n-2阶台阶的方法有dp[n-1]，dp[n-2]个
    // 所以最终爬n阶台阶的方法种类就是dp[n-1]+dp[n-2]

    int climbStairs(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        vector<int> dp(n+1);
        dp[1]=1;
        dp[2]=2;
        for(int i=3; i<=n; i++){
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

class Solution {
public:
    int climbStairs(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        return climbStairs(n-1)+climbStairs(n-2);
    }
};  //超时

题目：746. 使用最小花费爬楼梯

文章链接：代码随想录

视频链接：LeetCode:746.使用最小花费爬楼梯

题目链接：力扣题目链接

图释：

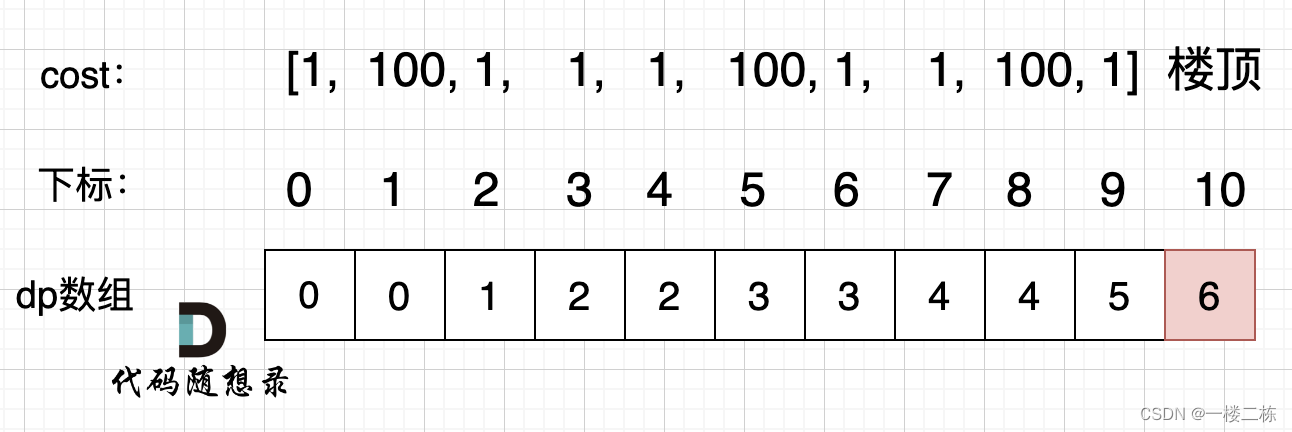
class Solution {
public:
    // 确定dp数组（dp table）以及下标的含义 vector<int> dp, dp[i]表示爬到第n层台阶的最低花费
    // 确定递推公式      dp[i]= min(dp[i-1]+cost[i-1], dp[i-2]+cost[i+2]) 可以选择从前一个台阶或者前两个台阶爬上来 
    // dp数组如何初始化  dp[0]=0, dp[1]=0  题目说了，可以选择从0或者1台阶出发，也就是dp[i]到这两个台阶的最低花费为0
    // 确定遍历顺序      从前往后
    // 举例推导dp数组 
    int minCostClimbingStairs(vector<int>& cost) {
        if(cost.size()==0 || cost.size()==1) return 0;
        vector<int> dp(cost.size()+1);
        dp[0]=dp[1]=0;
        for(int i=2; i<=cost.size(); i++){  // 顶楼表示为dp[n] 
            dp[i]= min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);
        }
        return dp[cost.size()];
    }
};