LeetCode刷题--- 二叉搜索树中第K小的元素
发布时间:2023年12月18日
个人主页:元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客
个人专栏
- 力扣递归算法题? ? ? ?【?http://t.csdnimg.cn/yUl2I? ?】
- 【C++】? ? ? ? ? ? ? ? ? 【?http://t.csdnimg.cn/6AbpV?】
- 数据结构与算法? ? ? ?【?http://t.csdnimg.cn/hKh2l? 】
前言:这个专栏主要讲述递归递归、搜索与回溯算法,所以下面题目主要也是这些算法做的 ?
我讲述题目会把讲解部分分为3个部分:
1、题目解析
2、算法原理思路讲解
3、代码实现
注意:这道题目涉及到二叉搜索树的内容 ,若有不懂的可以参考下面这篇文章?
二叉搜索树中第K小的元素
题目链接:二叉搜索树中第K小的元素
题目
给定一个二叉搜索树的根节点?root?,和一个整数?k?,请你设计一个算法查找其中第?k?个最小元素(从 1 开始计数)。
示例 1:
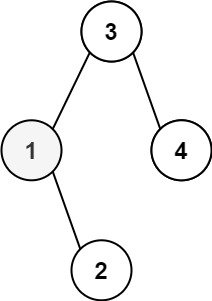
输入:root = [3,1,4,null,2], k = 1 输出:1
示例 2:
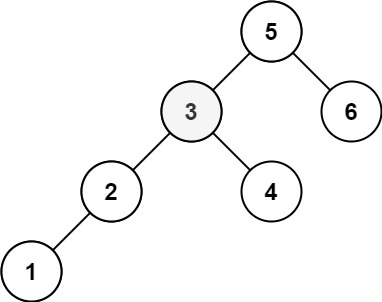
输入:root = [5,3,6,2,4,null,null,1], k = 3 输出:3
提示:
- 树中的节点数为?
n?。 1 <= k <= n <= 1040 <= Node.val <= 104
进阶:如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第?k?小的值,你将如何优化算法?
解法
题目解析
题目意思很简单,给我们一颗二叉搜索树,我们找出第 k 个最小的值(从 1 开始)
二叉搜索树有如下特性:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
?算法原理思路讲解??
解法一:
依靠二叉搜索树的特性:中序遍历为有序
思路:创建一个全局变量 v ,中序遍历整个二叉树,将搜索二叉树的值存入 v 中,然后再返回 v[k-1] 即可
解法二:
解法一虽然也可以通过,上述解法不仅使??量额外空间存储数据,并且会将所有的结点都遍历?遍。 我们没有必要遍历整个二叉搜索树。
但是,我们可以根据中序遍历的过程,只需扫描前 k 个结点即可。
思路:因此,我们可以创建?个全局的计数器 count,将其初始化为 k,每遍历?个节点就将 count--。直到某次递归的时候,count 的值等于 0 ,说明此时的结点就是我们要找的结果。
算法流程
1.定义?个全局的变量 count,在主函数中初始化为 k 的值
递归函数的设计
void?dfs(TreeNode* root);
2.递归函数流程(中序遍历)
(1)递归出?:root == nullptr 或 count=0 的时候,返回?
(2)先递归判断左?树,count--
(3)判断 count 是否为0,若为 0 则把 val 值赋给 ret
以上思路就讲解完了,大家可以先自己先做一下?
代码实现?
解法一
- 时间复杂度:预处理的时间复杂度为 O(N),其中 N 是树中结点的总数;我们需要遍历树中所有结点来统计以每个结点为根结点的子树的结点数。搜索的时间复杂度为 O(H),其中 H 是树的高度;当树是平衡树时,时间复杂度取得最小值 O(log?N);当树是线性树时,时间复杂度取得最大值 O(N)。
- 空间复杂度:O(N),用于存储以每个结点为根结点的子树的结点数。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public:
vector<int> v;
void dfs(TreeNode* root)
{
if (root == nullptr)
{
return;
}
dfs(root->left);
v.push_back(root->val);
dfs(root->right);
}
int kthSmallest(TreeNode* root, int k)
{
dfs(root);
return v[k-1];
}
};解法二
- 时间复杂度:O(H+k),其中 H 是树的高度。在开始遍历之前,我们需要 O(H) 到达叶结点。当树是平衡树时,时间复杂度取得最小值 O(log?N+k);当树是线性树(树中每个结点都只有一个子结点或没有子结点)时,时间复杂度取得最大值 O(N+k)。
- 空间复杂度:O(1)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int count;
int ret;
void dfs(TreeNode* root)
{
if(root == nullptr || count == 0) return;
dfs(root->left);
count--;
if(count == 0) ret = root->val;
dfs(root->right);
}
int kthSmallest(TreeNode* root, int k)
{
count = k;
dfs(root);
return ret;
}
};
文章来源:https://blog.csdn.net/weixin_74268082/article/details/134991399
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 台式电源质量如何检测?纳米软件为您科普
- MySQL一行记录是怎么存储的?
- Siamese network 孪生神经网络--一个简单神奇的结构
- 优雅而高效的JavaScript——Promise 和 async/await
- C++ //练习 1.11 编写程序,提示用户输入两个整数,打印出这两个整数所指定的范围内的所有整数。
- vim编辑器的使用
- 4步带你了解什么是归一化!
- 异常(C++)
- 回车与换行的区别。CR、LF、CRLF的区别。\r \n \r\n
- Android扫码方案