其他排序(基数排序,希尔排序和桶排序)(数据结构课设篇3,python版)(排序综合)
本篇博客主要详细讲解一下其他排序(基数排序,希尔排序和桶排序)也是排序综合系列里最后一篇博客。第一篇博客讲解的是LowB三人组(冒泡排序,插入排序,选择排序)(数据结构课设篇1,python版)(排序综合),第二篇博客讲解的是NB三人组(堆排序,归并排序,快速排序)(数据结构课设篇2,python版)(排序综合)。
random和time库的用法在第一篇冒泡排序里讲解过。数据结构课设实验内容和要求也在第一篇博客中。
基数排序:
概念:
基数排序是一种非比较型的排序算法,它根据数字的位数进行排序。它首先按照个位数进行排序,然后按照十位数进行排序,以此类推,直到最高位数。基数排序适用于整数或字符串的排序。假设待排序的数据有 n 个,每个数据的位数为 d,数据的范围为 k,那么基数排序的时间复杂度可以表示为 O(d*(n+k))。基数排序的基本思想是:
- 根据个位数进行排序,将数据分配到0-9的桶中。
- 按照顺序将桶中的数据合并起来。
- 根据十位数进行排序,再次将数据分配到0-9的桶中。
- 按照顺序将桶中的数据合并起来。 依次类推,直到最高位排序完成。
如图:

代码及详细注释:
import random
import time
def radix_sort(li):
max_num = max(li) # 找到列表中的最大值
it = 0 # 初始化迭代次数
while 10 ** it <= max_num: # 循环直到最高位
buckets = [[] for _ in range(10)] # 定义十个空桶
for val in li:
digit = (val // 10 ** it) % 10 # 取val的第it位数字(个位、十位、百位等)
buckets[digit].append(val) # 将val放入对应的桶中
# 分桶完成
li.clear()
for buc in buckets: # 将桶中的元素按顺序合并为一个列表
li.extend(buc)
# 把数重新写回li
it += 1 # 迭代次数加1
li = [random.randint(1, 100000000) for i in range(10000)]
print(li)
start = time.time()
radix_sort(li)
end = time.time()
print(li)
print('运行时间:%s Seconds'%(end-start))
基数排序的思想和代码都比较好理解,详细过程注释中都有说明。
运行结果:
希尔排序:
概念:
希尔排序是一种插入排序的改进版本,它通过将待排序的数据分成若干个小组,分别进行插入排序,然后逐渐减少小组的数量和增加小组内元素的间隔,直到最后一次将整个数据序列作为一个小组进行插入排序。希尔排序的时间复杂度在O(nlogn)和O(n^2)之间。希尔排序的基本思想是:
- 首先,选择一个增量序列,例如n/2、n/4、n/8等,将待排序的数据分成若干个小组。
- 然后,对每个小组内的数据进行插入排序。
- 接着,逐渐减少增量,重复上述步骤,直到增量为1,最后进行一次插入排序。
如图:
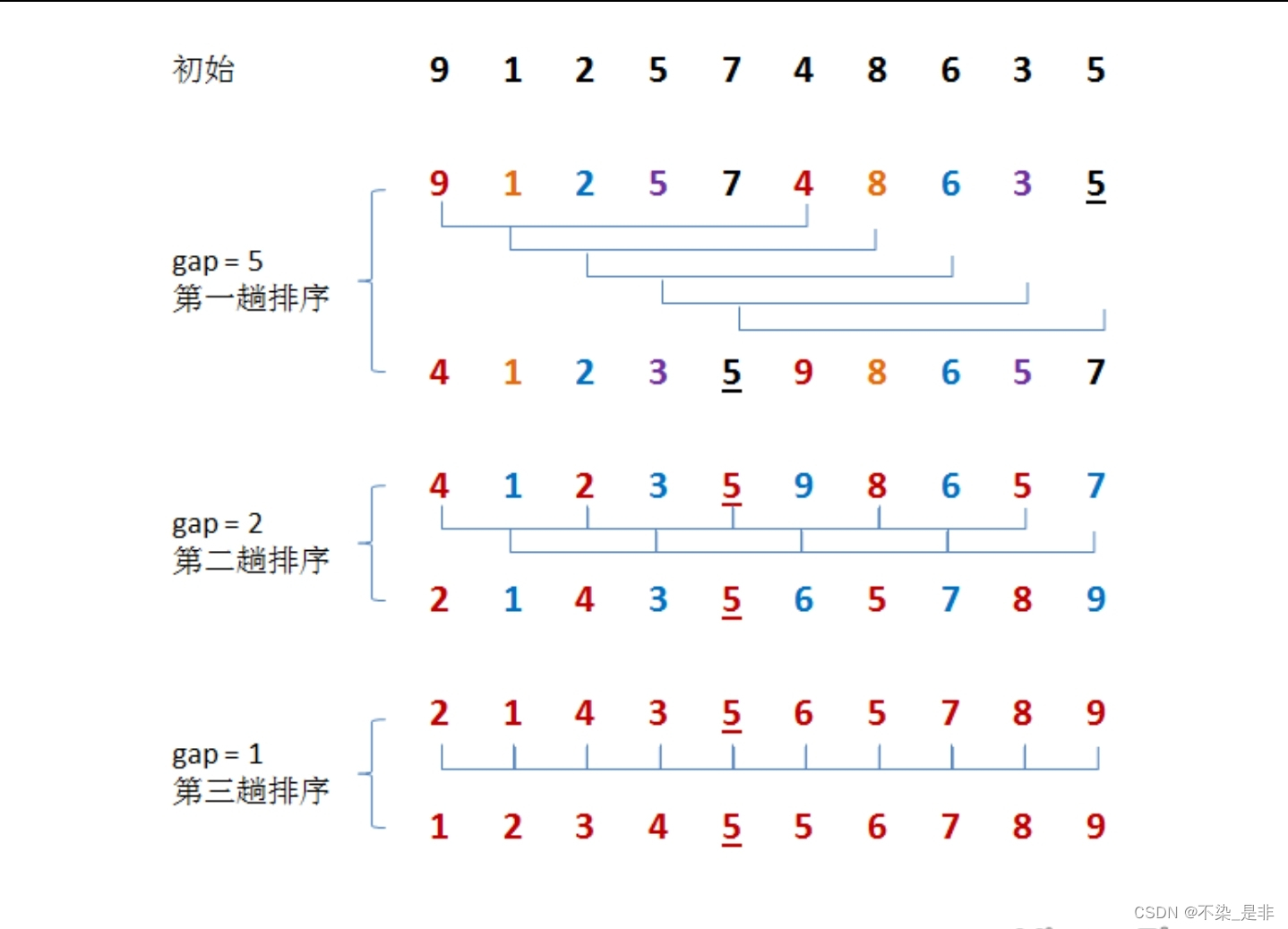
代码及详细注释:
import random
import time
def insert_sort_gap(li, gap):
for i in range(gap, len(li)): # 从第gap个元素开始,依次向前进行插入排序
j = i - gap # j指向当前元素的前一个元素
tmp = li[i] # 记录当前元素的值
while j >= 0 and li[j] > tmp: # 如果前面的元素比当前元素大
li[j + gap] = li[j] # 将前面的元素后移gap位
j -= gap # 继续向前寻找插入位置
li[j + gap] = tmp # 插入当前元素到正确的位置
def shell_sort(li):
d = len(li) // 2 # 初始步长取数组长度的一半
while d >= 1:
insert_sort_gap(li, d) # 对每个步长进行插入排序
d //= 2 # 步长减半
li = [random.randint(1, 100000000) for i in range(100000)]
print(li)
start = time.time()
shell_sort(li)
end = time.time()
print(li)
print('运行时间:%s Seconds'%(end-start))
希尔排序的思路和代码也是比较好理解和实现的,注释里讲解的还是比较详细的。
运行结果:
桶排序:
概念:
桶排序是一种排序算法,它将待排序的数据分成若干个桶,然后对每个桶内的数据进行排序,最后将所有桶内的数据按照顺序合并起来。桶排序适用于待排序的数据分布比较均匀的情况下。
桶排序的时间复杂度取决于使用的排序算法和桶的数量。在最理想的情况下,桶排序的时间复杂度为O(n+k),其中n是待排序元素的数量,k是桶的数量。这是因为在最理想的情况下,每个桶中的元素都是均匀分布的,因此每个桶内的排序所需的时间是O(1)。然而,在最坏的情况下,所有元素都被放入同一个桶中,此时桶排序的时间复杂度将变为O(nlogn),这是因为在这种情况下需要使用其他的排序算法对桶内的元素进行排序。
桶排序的基本思想是:
- 首先,确定桶的数量,并将待排序的数据分配到对应的桶中。
- 然后,对每个桶内的数据进行排序,可以使用任何一种排序算法,通常使用插入排序或者快速排序。
- 最后,按照桶的顺序将所有桶内的数据合并起来。
如图:
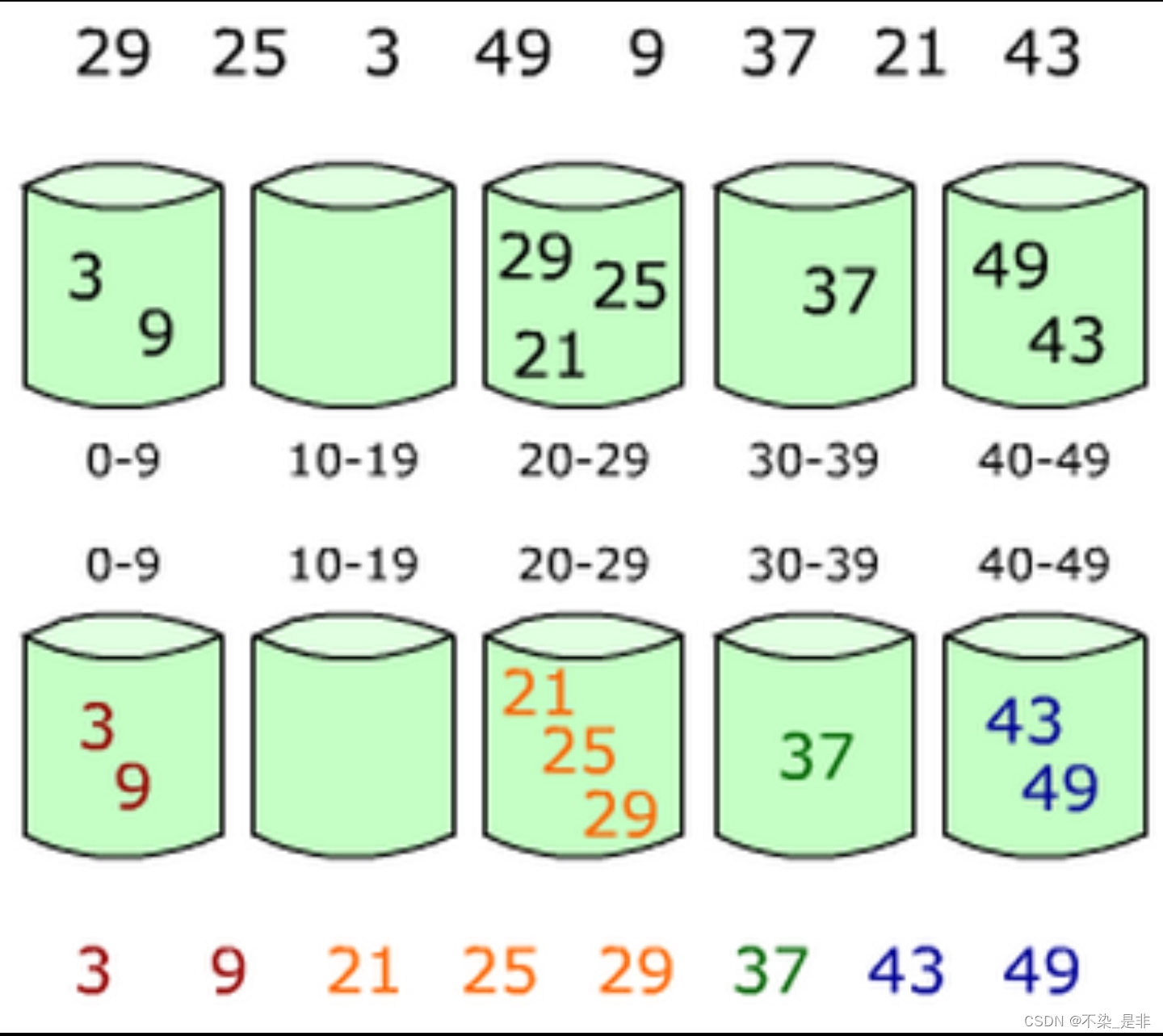
代码及详细注释:
import random
import time
def bucket_sort(li, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建n个空桶
for val in li:
i = min(val // (max_num // n), n - 1) # 计算val应该放到哪个桶里
buckets[i].append(val) # 将val加入对应的桶中
# 保持桶内的顺序
for j in range(len(buckets[i]) - 1, 0, -1): # 对桶内元素进行排序
if buckets[i][j] < buckets[i][j - 1]: # 如果当前元素比前一个元素小
buckets[i][j], buckets[i][j - 1] = buckets[i][j - 1], buckets[i][j] # 交换两个元素的位置
else:
break # 如果当前元素大于等于前一个元素,则停止排序
sorted_li = []
for buc in buckets: # 将所有桶中的元素按顺序合并为一个列表
sorted_li.extend(buc)
return sorted_li # 返回排序后的列表
li = [random.randint(1, 100000000) for i in range(10000)]
print(li)
start = time.time()
bucket_sort(li)
end = time.time()
print(li)
print('运行时间:%s Seconds'%(end-start))
运行结果:
总结:
至此排序综合系列讲解完毕,排序综合1讲解了LowB三人组(冒泡排序,插入排序,选择排序)(数据结构课设篇1,python版)(排序综合),排序综合2讲解了NB三人组(堆排序,归并排序,快速排序)(数据结构课设篇2,python版)(排序综合)。这些也是数据结构的课设之一,大家可以借鉴参考一下。总体来说排序的思路和代码还是相对与其他算法好理解和实现的
在这里我也给大家对所有讲过的排序进行一个运行效率上的比较(不是通过时间复杂度而是通过运行结果),在此之前每个排序我都对好几组不同内容和不同规模大小的数组进行排序运行,最后得出的结果是:桶排序和冒泡排序最慢,其次是插入排序和选择排序,再次是希尔排序,最后是基数排序,堆排序,归并排序和快速排序(其中基数排序在大规模运算下效率高,运行时间最短)如有不对,欢迎指正。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 国漫风向标!2023年玄机科技斩获6项腾讯金鹅荣誉
- 池化层(pooling)
- 【centos 安装配置nginx】nginx负载均衡、限流配置
- 【重点问题】攻击面发现及管理
- python解决动态规划算法问题,爬楼梯问题
- windows----Vmware虚拟机安装ubuntu
- 洛谷700题 - 1 校门外的树
- (三)SQL优化与索引使用
- Codeforces Round 919 (Div. 2)(A-D)
- 【LinuxC】进程(未完)