互联网加竞赛 python opencv 深度学习 指纹识别算法实现

1 前言

🔥 优质竞赛项目系列，今天要分享的是

🚩 python opencv 深度学习 指纹识别算法实现

🥇学长这里给一个题目综合评分(每项满分5分)

• 难度系数：3分
• 工作量：4分
• 创新点：4分

该项目较为新颖，适合作为竞赛课题方向，学长非常推荐！

🧿 更多资料, 项目分享：

https://gitee.com/dancheng-senior/postgraduate

2 指纹识别方式

目前市面上有两种指纹识别，分别是光学式和电容式指纹识别。

2.1 电容式指纹识别

电容式指纹识别要比光学式的复杂得多，其原理是将压力感测、电容感测、热感测等感测器整合于一块芯片中，当指纹按压芯片表面时，内部电容感测器会根据指纹波峰与波谷而产生的电荷差（或是温差），形成指纹影像，再通过与算法内部的指纹库进行匹配，从而完成指纹识别。

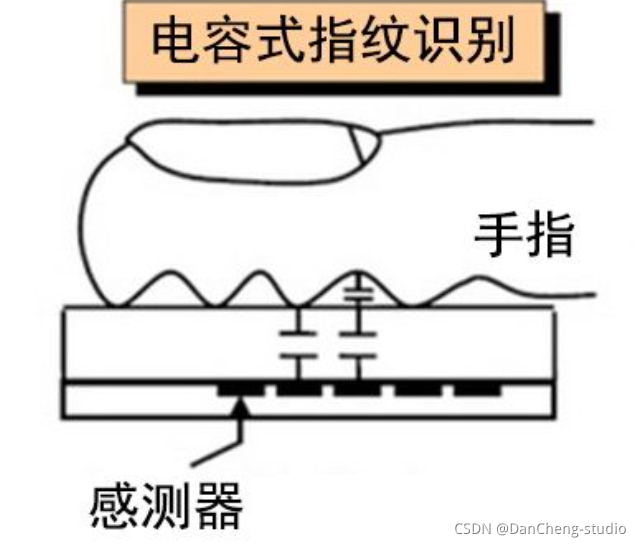
电容式指纹识别技术较为复杂，对技术研发和积累有较高要求，并且涉及大量专利，算法得实现也相对困难，所以目前全球只有少数公司能在这方面提供领先的技术产品。

2.2 光学式指纹识别

然后是光学式指纹识别，大家常见的指纹考勤机就是光学式指纹识别。

这类光学式指纹识别主要包括4个方面功能

• 1.指纹模块负责采集指纹图像。
• 2.数字信号处理器主要把采集到的指纹图像转化为数字信号。
• 3.微控制器是整个系统的控制单元，在这里将进行指纹的验证以及输出指令。
• 4.液晶显示器将输出指纹验证结果。

当我们把手指放在指纹考勤机上时，通过镜面反射原理，指纹模块就会采集指纹图像

接着指纹图像就会被数字信号处理器转换成数字信号

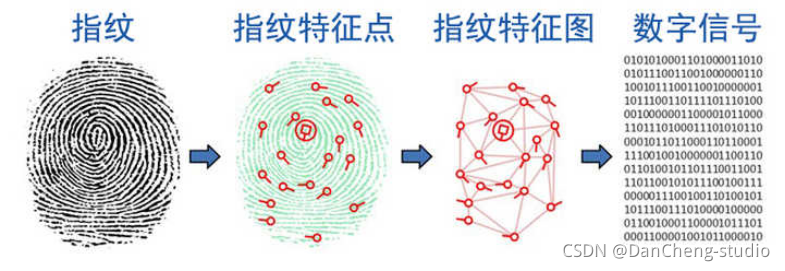
然后通过微控制器将数字信号与指纹库里的指纹进行匹配，匹配结果将通过液晶显示器显示出来。这就是光学式指纹识别的工作原理。

电容式与光学式指纹识别主要在指纹的采集方式上拥有较大差异，而在指纹的验证过程中则基本类似。然而因为电容式指纹识别拥有体积小、适用性广的优点，已经有越来越多的设备采用电容式指纹识别，未来的主流将是电容式指纹识别。

3 指纹识别算法实现

3.1 指纹识别算法流程

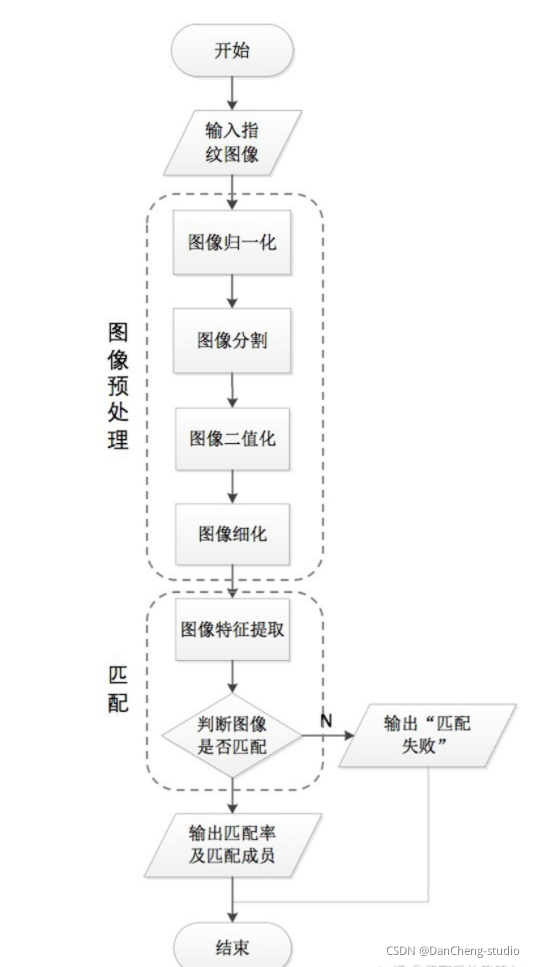
3.2 指纹图像预处理

• 1.图像归一化
• 2.图像分割
• 3.图像二值化
• 4.细化

几个步骤 当然有一些算法为了追求极致，中间还利用了增强、多重滤波等方式，但最根本的目的都是为了在细化之后保留指纹信息并且方便后续处理。

预处理之后是特征点的提取，也就是找到指纹图像当中有价值，具有唯一性和不变性的信息。主要特征点有端点、分叉点几类，在提取部分除了简单的遍历检索确认之外，还有比较重要的一步是伪特征点的去除，主要是针对图像不清晰、不完整导致的断点和边缘端点等。

最后一步是特征点的匹配，将指纹库中的指纹信息与提取的目标图像特征点进行对比。主流算法是以指纹中心点为依据，根据特征点所在的角度及距离，确认其所在位置，根据匹配度计算是否是同一手指的指纹。

3.3 指纹图像目标提取

指纹图像目标提取主要是将指纹图片中提取出来，也叫做指纹图像分割。

图片的前景通过观察可知是由条状或者圆形的一些组成，而底图其他部分只是一个均匀的底色而已。

我们使用非常简单的手段，基于局部梯度就可以很容易实现我们的目标。

方差梯度法提取指纹:

指纹图像通常由前景区域（包含有指纹的脊线和谷线）和背景区域这两部分组成。一般来说，在指纹图像的前景区域中，指纹的脊线和谷线的灰度差是较大的，因而其灰度统计特性局部灰度方差很大；而在指纹图像的背景区域中，两者的方差是很小的。基于这一特性，可以利用指纹图像的局部方差来进行分割。因此，这种方法也被称为方差梯度法。

的灰度平均值 M和方差 Var计算方法：

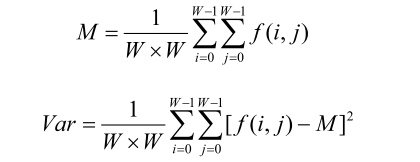
提取前的指纹图像：

提取后的指纹图像：

可以看到，学长做的还有些噪点，但是也很好解决，做一次形态学操作即可：

这样噪点就去除了。

3.4 指纹图像增强

3.5 指纹特征提取

人体指纹的特征可以反映在给定的人类群体里来自不同手指的指纹之间相似的程度。

指纹的特征信息很多，所有的这些指纹特征信息构成了庞大的指纹特征集合。

指纹的细节特征主要指的是纹线端点（RidgeEnding）和纹线分叉点（RidgeBifurcation）。

纹线端点指的是纹线突然结束的位置，而纹线分叉点则是指纹线一分为二的位置。

大量的统计结果表明，使用这两类特征点就足以描述指纹的唯一性。

Minutia Cylinder-Code (MCC) ，该算法是非常著名的指纹特征识提取算法，

第一次发表在：IEEE tPAMI

Minutia Cylinder-Code: a new representation and matching technique for
fingerprint recognition", IEEE tPAMI 2010

• MCC提出了一种基于三维数据结构的圆柱编码算法，其从细节的距离和角度出发，构造了圆柱编码
• 为一种多级的指纹匹配方法，其不仅使用了细节点特征也使用了方向场等特征
• 特征视为一种局部结构，也是3D结构

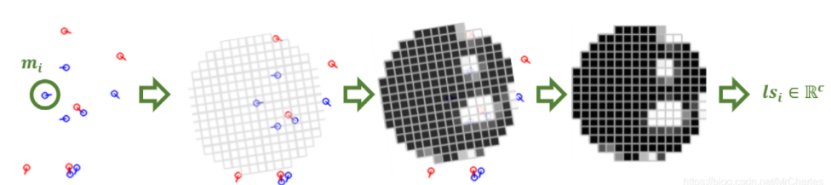
部分实现代码：

    
?    # Compute the cell coordinates of a generic local structure
?    # 计算
?    mcc_radius = 70
?    mcc_size = 16
?    

g = 2 * mcc_radius / mcc_size
x = np.arange(mcc_size)*g - (mcc_size/2)*g + g/2
y = x[..., np.newaxis]
iy, ix = np.nonzero(x**2 + y**2 <= mcc_radius**2)
ref_cell_coords = np.column_stack((x[ix], x[iy]))
    mcc_sigma_s = 7.0
    mcc_tau_psi = 400.0
    mcc_mu_psi = 1e-2
    

def Gs(t_sqr):
    """Gaussian function with zero mean and mcc_sigma_s standard deviation, see eq. (7) in MCC paper"""
    return np.exp(-0.5 * t_sqr / (mcc_sigma_s**2)) / (math.tau**0.5 * mcc_sigma_s)

def Psi(v):
    """Sigmoid function that limits the contribution of dense minutiae clusters, see eq. (4)-(5) in MCC paper"""
    return 1. / (1. + np.exp(-mcc_tau_psi * (v - mcc_mu_psi)))


?    
?    
?    
?    # n: number of minutiae
?    # c: number of cells in a local structure
?    

xyd = np.array([(x,y,d) for x,y,_,d in valid_minutiae]) # matrix with all minutiae coordinates and directions (n x 3)

# rot: n x 2 x 2 (rotation matrix for each minutia)

d_cos, d_sin = np.cos(xyd[:,2]).reshape((-1,1,1)), np.sin(xyd[:,2]).reshape((-1,1,1))
rot = np.block([[d_cos, d_sin], [-d_sin, d_cos]])

# rot@ref_cell_coords.T : n x 2 x c

# xy : n x 2

xy = xyd[:,:2]

# cell_coords: n x c x 2 (cell coordinates for each local structure)

cell_coords = np.transpose(rot@ref_cell_coords.T + xy[:,:,np.newaxis],[0,2,1])

# cell_coords[:,:,np.newaxis,:]      :  n x c  x 1 x 2

# xy                                 : (1 x 1) x n x 2

# cell_coords[:,:,np.newaxis,:] - xy :  n x c  x n x 2

# dists: n x c x n (for each cell of each local structure, the distance from all minutiae)

dists = np.sum((cell_coords[:,:,np.newaxis,:] - xy)**2, -1)

# cs : n x c x n (the spatial contribution of each minutia to each cell of each local structure)

cs = Gs(dists)
diag_indices = np.arange(cs.shape[0])
cs[diag_indices,:,diag_indices] = 0 # remove the contribution of each minutia to its own cells

# local_structures : n x c (cell values for each local structure)

local_structures = Psi(np.sum(cs, -1))

3.6 指纹识别结果

提取特征后，剩下的任务就是对特征进行分类了，可以使用的算法就很多了，比如svm，决策树、神经网络，都可以

4 整体效果

5 最后

🧿 更多资料, 项目分享：

https://gitee.com/dancheng-senior/postgraduate