【数据结构】(二叉树)计算结点|叶子结点|高度|第K层结点数
 ?
?
目录
?
概念:
一颗二叉树是结点的一个有限集合,该集合:
1.或者为空;
2.由一个根节点加上两棵别称为左子树和右子树的二叉树组成;
注:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
 ?
?
特殊的二叉树
1. 满二叉树:?一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。
注:满二叉树是一种特殊的完全二叉树。
二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点;
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2^(h-1);
3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有n0?=n2 +1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度h = log2(n+1); (是以2为底数,(n+1)为对数)
二叉树的存储结构
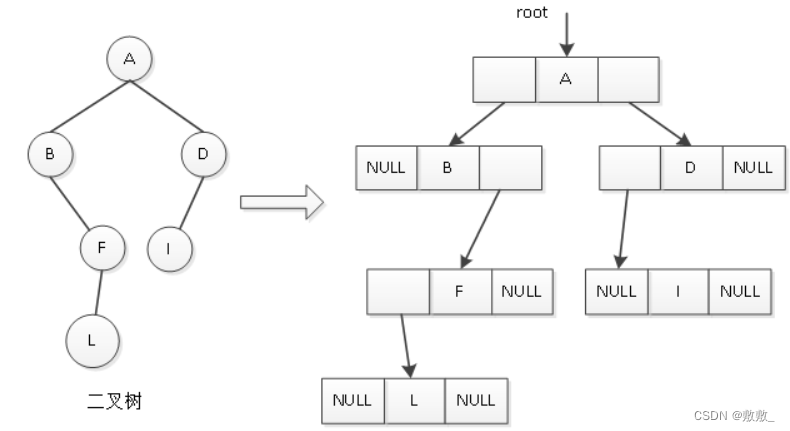
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。?
1. 顺序存储?:
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储;
二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。?
2. 链式存储 :
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域;
左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
 ?
?
顺序存储在?【数据结构】——堆|Top-k|堆排序-CSDN博客
本节着重介绍链式存储;
二叉树的创建
作者水平有限,目前只能手动创建一颗伪二叉树?
?创建链表结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data; //数据域
struct BinaryTreeNode* left; //左子树
struct BinaryTreeNode* right; //右子树
}TreeNode;手动快速创建一个二叉树?
//创建一个结点
TreeNode* BuyTreeNode(BTDataType x)
{
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
// 构建树
TreeNode* CreateTree()
{
TreeNode* node1 = BuyTreeNode(1);
TreeNode* node2 = BuyTreeNode(2);
TreeNode* node3 = BuyTreeNode(3);
TreeNode* node4 = BuyTreeNode(4);
TreeNode* node5 = BuyTreeNode(5);
TreeNode* node6 = BuyTreeNode(6);
TreeNode* node7 = BuyTreeNode(7);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
//增加一个结点
//node5->right = node7;
//返回根结点
return node1;
} ?
?
二叉树遍历?
二叉树遍历分为:前序,中序,后序遍历;
前序:访问根结点的操作发生在遍历其左右子树之前;
中序:访问根结点的操作发生在遍历其左右子树中间;
后序:访问根结点的操作发生在遍历其左右子树之后;
注:为了理解透彻,访问到NULL才结束子树的遍历;
前序:
?前序遍历是先访问根节点,再访问左子树,左子树根结点访问完后 才会访问左子树结点然后右子树结点;

void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
//前序
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}N表示NULL,方便理解?
 ?
?
中序:
先行访问左子树,只有左子树访问完后才会访问子树根节点
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
//中序
PrevOrder(root->left);
printf("%d ", root->data);
PrevOrder(root->right);
} ?
?
后序:
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
//后序
PrevOrder(root->left);
PrevOrder(root->right);
printf("%d ", root->data);
}
?计算结点数
?递归的核心思想是: 1.子问题分治,
????????????????2.返回条件(递归条件);
1.子问题分治:计算这棵树的结点数,可以理解 左子树结点数+右子树结点数 + 根节点;
左子树结点数又可以分为 左子树结点数+右子树结点数 +子树根节点;
右子树同理;
如何结束递归循环呢?
2.返回条件:遇到结点为NULL,?
 ?
?
//计算树的结点数
int TreeSize(TreeNode* root)
{
if (root == NULL)
return 0;
return ((TreeSize(root->left) + TreeSize(root->right)) + 1);
}计算叶子结点数
叶子结点:没有左右子树的结点;
1.分治:左子树叶子结点数+右子树结点数;
2.返回条件: 如果结点为NULL,返回0;
? ? ? ?如果该结点左右子树为NULL,返回1;
否则往下寻找 直至遇到返回条件;
 ?
?
 ?
?
//计算叶子结点数
int TreeLeafSize(TreeNode* root)
{
//空 返回0
if (root == NULL)
return 0;
//结点 返回1
if (root->left == NULL && root->right == NULL)
return 1;
//非空 非结点, 说明下面还有结点 左子树+右子树
return TreeLeafSize(root->left)
+ TreeLeafSize(root->right);
}计算树的高度(深度)
1.分治:计算左右子树的高度,选择较大数+1 ;
2.递归条件:只有遇到NULL,就表明到该子树尾;
 ?
?
 ?
?
注:三目比较法会造成极大的负担,因为比较大小后,程序并没有记住较大值是多少,会重复访问;?
//计算树的高度
int TreeHeight(TreeNode* root)
{
if (root == NULL)
return 0;
//return (TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) : TreeHeight(root->right)) + 1;
return fmax(TreeHeight(root->left),
TreeHeight(root->right)) + 1;
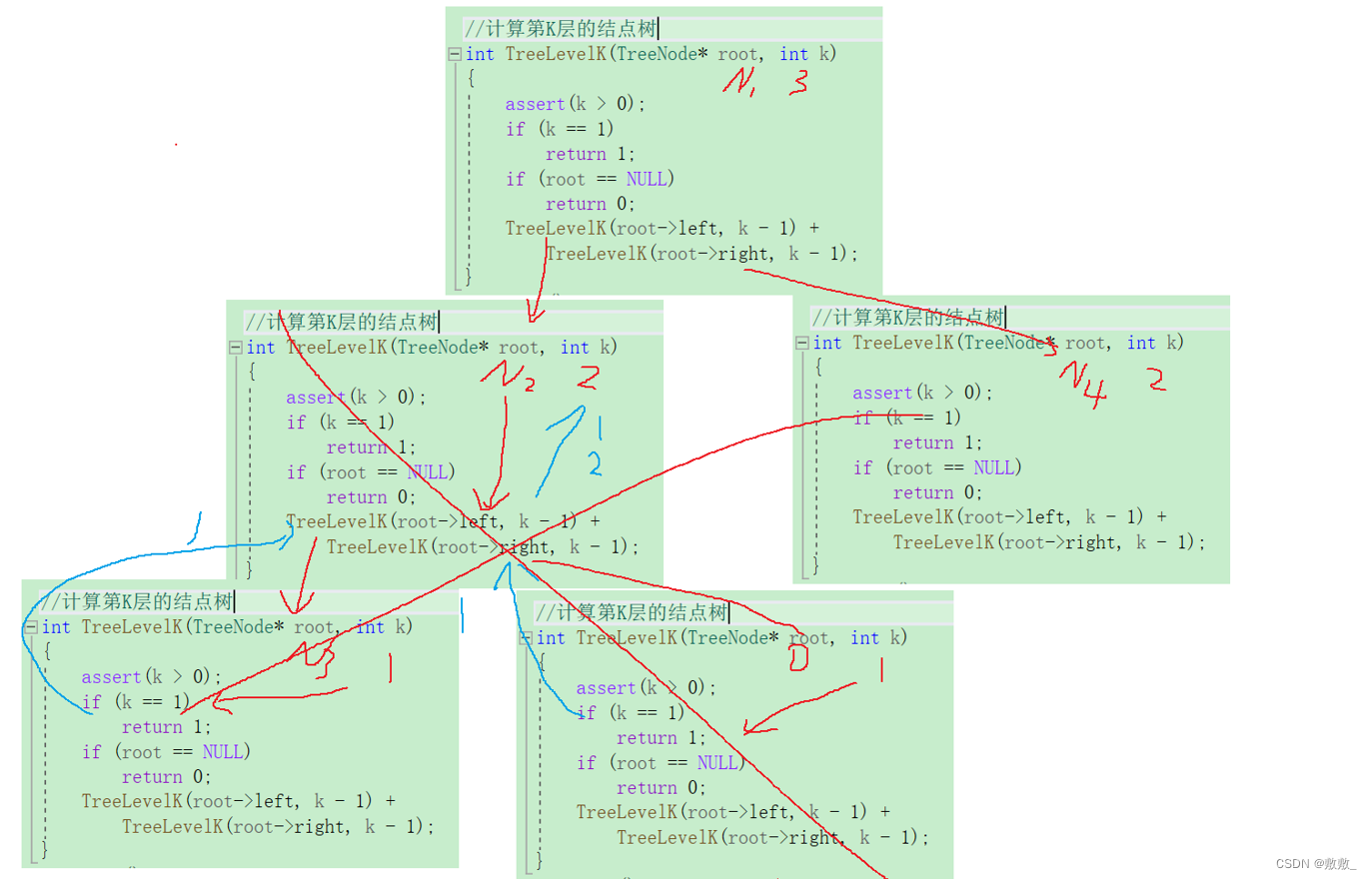
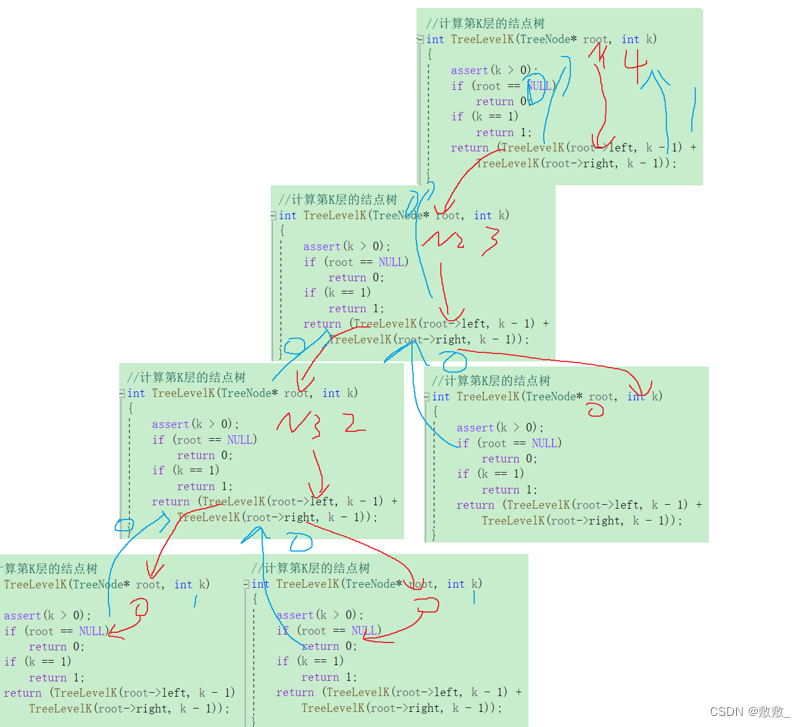
}计算第K层结点数
计算第K层,相当于计算子树的第K-1层;
注:当K == 1时,要确保该结点存在,所以先行判断结点是否存在,再判断K是否等于1;
 ?
?

 ?
?

//计算第K层的结点树
int TreeLevelK(TreeNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return (TreeLevelK(root->left, k - 1) +
TreeLevelK(root->right, k - 1));
}

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- java爬虫(jsoup)如何设置HTTP代理ip爬数据
- 【职工管理系统(C++版)】
- 代码随想录算法训练营第二十五天 | 216.组合总和III、17.电话号码的字母组合
- Linux 系统上,你可以使用 cron 定时任务来定期备份 MySQL 数据库
- Jmeter(七) - 从入门到精通 - 建立数据库测试计划实战<MySQL数据库>(详解教程)
- 第七章 Jsp
- GZ015 机器人系统集成应用技术样题8-学生赛
- 虾皮购物利器:Shopee买家通系统完美解密
- LeetCode150. 逆波兰表达式求值
- 13-设计可综合状态机的指导原则