学校“数据结构”课程Project—扩展功能（自主设计）

目录

一、设想功能描述

想法缘起

目标功能

二、问题抽象

三、算法设计和优化

1. 易想的朴素搜索 / dp

搜索想法

动态规划（dp）想法

2. 思考与优化

四、算法实现

五、结果示例

附：使用的地图API

---

一、设想功能描述

想法缘起

• OSM 导出的地图数据中有 “amenity”（便民设施）点，并在 <tag k="amenity" v="..."/> 中标记了每个 amenity 的具体类型，比如：fast_food, pub, toilets……

• 而人们在路途或旅途中，常常关注最近的某种类型（常为 amenity，如卫生间、停车车场）的最近处，而尚未明确目的地。从而容易想到去设计一个扩展功能：给定 amenity，查询距离当前点最近的该类的点。显然，这个问题仍用 Dijkstra 求单源最短路即可。

• 然而，有时人们想连续去多个便民点，比如：先去停车场停车再去吃饭，最后逛逛周边的公园等等。为了提高效率与体验，很可能需要一个总路程最短的方案，这就是功能二考虑的问题。

目标功能

★ 用户给定当前位置，并指定一个 amenity 种类的顺序。求出最短路线，并呈现在地图上。

二、问题抽象

地图上有某些点带有颜色。给出起点 s 与颜色序列?，尽可能快地求出一条以 s 为起点的最短路线 ，要求其依次经过颜色为 的点。

存在数据约束与特征：，其中 为 颜色点集，此外，各种颜色的点大致均匀分布。

三、算法设计和优化

1. 易想的朴素搜索 / dp

搜索想法

直接以每个 为阶段，进行深度优先搜索（DFS），这部分时间复杂度已经有 ，虽然可以进行剪枝，即当前搜素的长度 cur 超过搜到的最短长度 res，就直接 return，但光这样时间复杂度不变的。

动态规划（dp）想法

以每个 为阶段设计 dp，易得状态转移方程类似如下形式：

然而，显然其时间复杂度是同搜索的，而且还很难剪枝，所以比搜索更差。

此外，还要计算中间相邻颜色两点的最短路，从而全求出来的时间复杂度应比上面更大，空间复杂度亦大。

2. 思考与优化

直观地，最终答案的路线几乎不可能 “兜得很远”，这启发我们优化搜索顺序。对于每个?，我们考虑先走到离最近的 搜索下去，回溯后再搜次近的 ……可以想象这样搜出来的前几条路已经得到或较接近最终答案。进一步来看，又因为各种颜色的点大致均匀分布，所以这样的剪枝效果一定是非常显著的。

不过，如何求出搜 的顺序？其实我们完全不必先预处理出最短路然后排序。注意到 Dijkstra 的最短路算法就是按照距离由到达的顺序得到 “确定点” 的。所以，我们把 Dijkstra 算法 “嵌入” 搜索框架之中，从当前 ?做 Dijkstra，遍历到一个下一颜色的 ，我们就从 递归进行搜索。这样相当于又解决了花大代价计算最短路的问题。

总之，本问题基于搜索的大框架，而其内部融入 Dijkstra，每个结点处的下一个点通过 Dijkstra 确定，当前搜索路上的每个点都保留了一个 Dijkstra 状态。

四、算法实现

关键在于构建搜索的代码，尤其是解决 “每一层” 都在做 Dijkstra 带来的问题。

原始 Dijkstra 只有一个答案数组 d[MAXN] ，这里我们显然需要多个，不过我们若开 n 个这样的数组，内存开销较大，且可能不易扩展。注意到 {d[u], u} 保留在原始 Dijkstra 的 std::priority_queue 中，我们可以用 std::set 代替这个 std::priority_queue，既可以取出最小值，又存下来当前有用的 {d[u], u} 且能 std::find 得到 {d[v], v}，而 vis 数组可用 std::unordered_set 代替。

这样，我们相当于仅在搜索路上开 C++ 的容器，空间开销显著减小而并未增大过多增加时间常数，且易于扩展。

void DFS(int s, int x, double cur) {
 ? ?if (x == Ord.size()) { // ... }
 ? ?set<pair<double, int>> d; d.insert({0.0, s});
 ? ?unordered_set<int> vis;
 ? ?while (d.size()) {
 ? ? ? ?int u = d.begin()->second;
 ? ? ? ?double dis = d.begin()->first;
 ? ? ? ?if (cur + dis > ans) return;
?
 ? ? ? ?d.erase(d.begin());
 ? ? ? ?if (vis.find(u) != vis.end()) continue;
 ? ? ? ?vis.insert(u);
 ? ? ? ?auto itt = M.p[u].Ames.find(Ord[x]);
 ? ? ? ?if (itt != M.p[u].Ames.end()) {
 ? ? ? ? ? ?curOrd.push_back(u);
 ? ? ? ? ? ?DFS(u, x+1, cur+dis);
 ? ? ? ? ? ?curOrd.pop_back();
 ? ? ?  }
?
 ? ? ? ?for (int e = M.head[u]; e; e = M.nxt[e]) {
 ? ? ? ? ? ?// ...
 ? ? ? ? ? ?auto it = d.upper_bound({-1.0, v});
 ? ? ? ? ? ?if (it==d.end() || it->second!=v || dis+w<it->first) d.insert({dis+w, v});
 ? ? ?  }
 ?  }
}

五、结果示例

• n=6：起点在徐家汇一带，（较为随意地）指定下面 6 个 Amenity Type 的顺序：

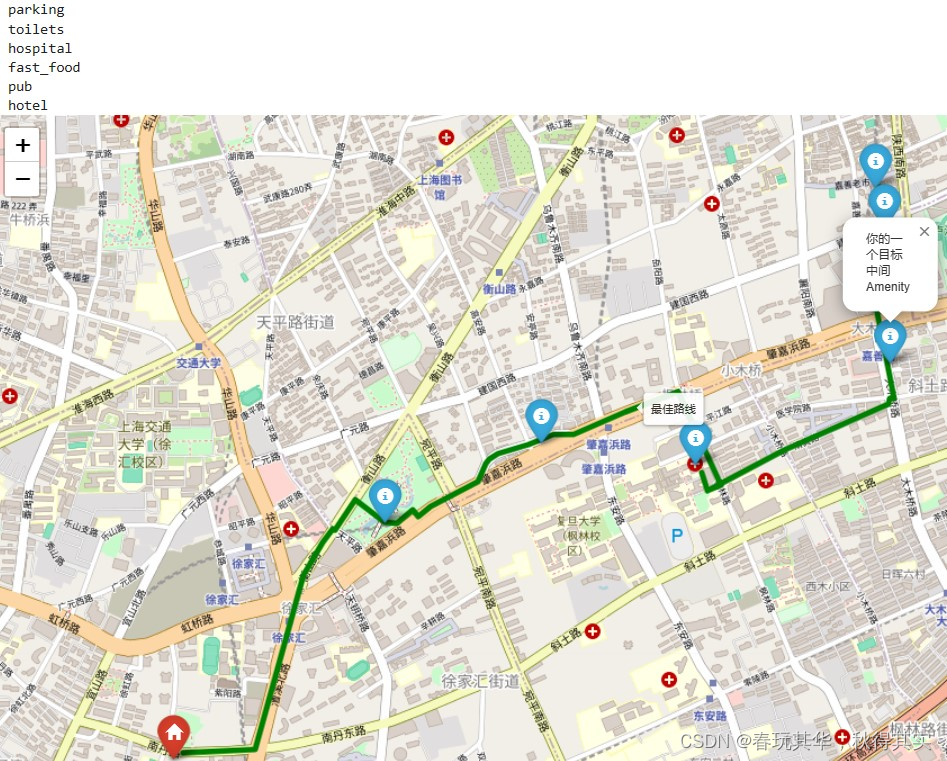
附：使用的地图API

????????基于 Leaflet.js 库的 Python 交互式地图包?Folium