深度学习理论方法：相似度计算

发布时间：2024年01月14日

? ? ? ?深度学习理论中的相似度计算，是衡量两个输入之间相似性或关联性的重要方法。它常用于比较输入是否相似或相关，广泛应用于推荐系统、图像识别、自然语言处理等领域。

? ? ? ?通过相似度计算，我们能更好地了解数据的内在结构和关系，从而进行更高效的数据分析和处理。例如，在自然语言处理中，利用相似度计算可以比较两个文本的语义相似度，进而实现文本分类、聚类、情感分析等任务。而在图像识别领域，借助相似度计算可以比较两个图像的相似程度，从而实现图像检索、人脸识别等任务。相似度的是计算方法很多，选用常用的两种进行学习，即欧几里得相似度和余弦相似度计算。

基于欧几里得距离的相似度计算

欧几里得距离是常用计算距离的公式，它用来表示三维空间中两个点的真实距离。在相似度计算中，不同的物品或者用户可以将其定义为不同的坐标点，而特定目标定位坐标原点，使用欧几里得距离计算两个点之间的绝对距离。公式如下：

$d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

由于在欧几里得相似度计算中，最终数值的大小与相似度成反比，因此在实际中常常使用欧几里得距离的倒数作为相似度值，即? $\frac{1}{d}+1$ ?作为近似值。

示例

表1? 用户对物品评分表
	物品1	物品2	物品3	物品4
用户1	1	1	3	1
用户2	1	2	3	2
用户3	2	2	1	1

如上图所示，如果需要计算用户1和其他用户之间的相似度，通过欧几里得距离公式可以得出：

用户1、用户2：?

$d_{12} = \sqrt{(1-1)^2+(1-2)^2+(3-3)^2+(1-3)^2}\approx 1.414$

?近似值 =? $\frac{1}{d_{12}}+1\approx 1.7$

?用户1、用户3：

$d_{13} = \sqrt{(1-2)^2+(1-2)^2+(3-1)^2+(1-1)^2}\approx 2.287$

?近似值 =? $\frac{1}{d_{13}}+1\approx 1.43$ ?

从以上结果可以看出，d12分值大于d13的分值，因此可以得出用户2与用户1更加相似。?

基于余弦角度的相似度计算

? ? ? ?

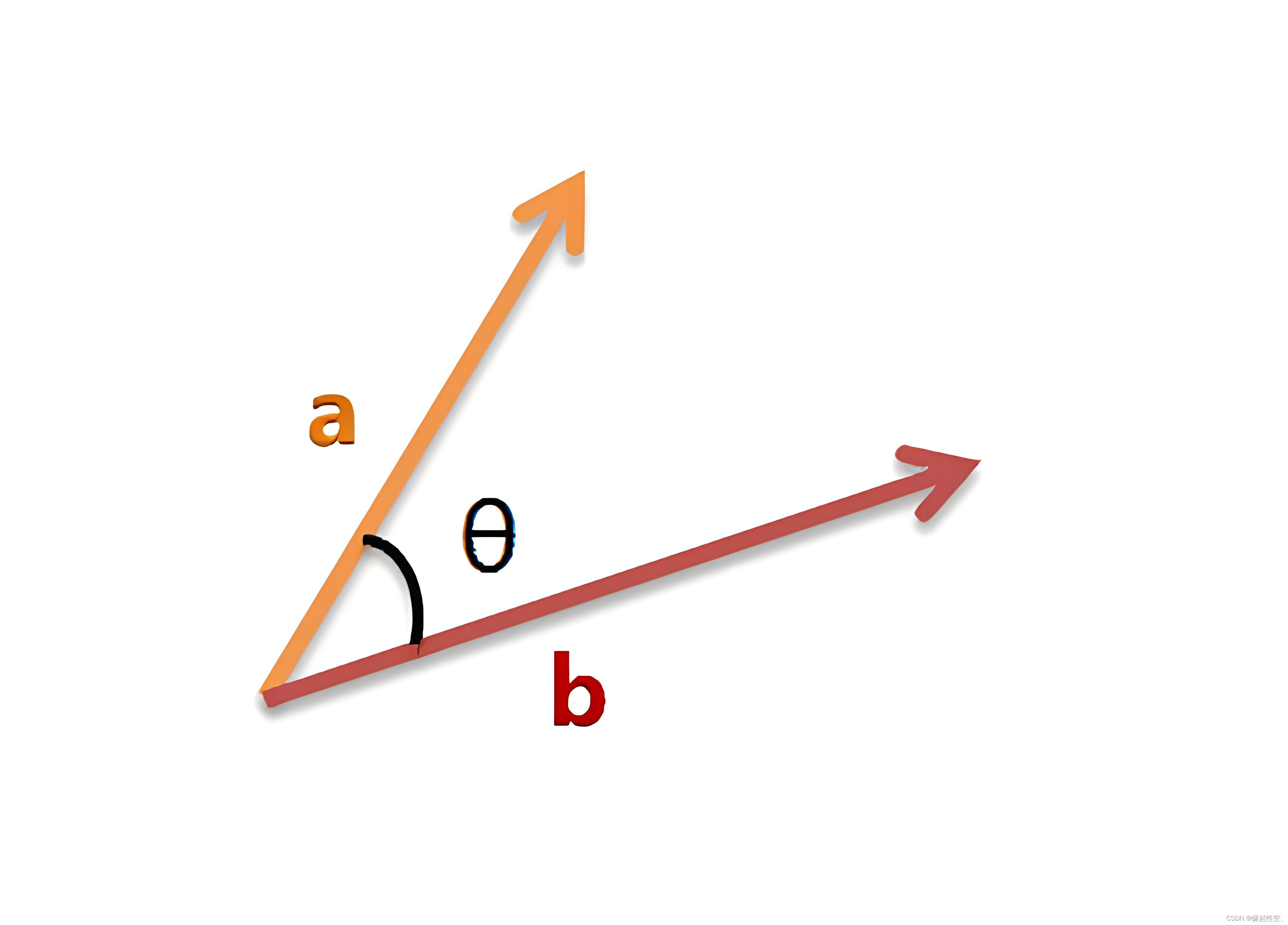
? ? ? ?与欧几里得距离相类似，余弦相似度也将特定目标作为坐标上的点（不是原点），与特定的被计算目标进行夹角计算。从上图可以明显看出，两条直线分别从坐标原点出发，引出一定的角度，如果两个目标较为相似，其形成夹角较小，反之夹角较大。因此在使用余弦度量的相似度计算中可以用夹角的大小反映目标之间的相似性。公式如下：

$cos@=\frac{\sum x_i\times y_i}{\sqrt{\sum x^2_i\times \sqrt{\sum y^2_i}}}$ ?

从公式可以看出，余弦值一般在[-1,1]之间，这个值的大小同时与余弦夹角的大小成正比。

如果用余弦相似度计算表1中用户1与用户2之间相似性：

$d_{12} = \frac{1\times 1+1\times 2+3\times3+1\times2}{\sqrt{1^2+1^2+3^2+1^2}\times\sqrt{1^2+2^2+3^2+2^2}}=\frac{14}{\sqrt{12}\times \sqrt{18}}\approx 0.789$

用户1与用户3之间的相似性：

? $d_{13} = \frac{1\times 2+1\times 2+3\times1+1\times1}{\sqrt{1^2+1^2+3^2+1^2}\times\sqrt{2^2+2^2+1^2+1^2}}=\frac{8}{\sqrt{12}\times \sqrt{10}}\approx 0.344$ ?

从以上计算可得，用户2相对于用户3，与用户1更为相似。?

总结?

? ? ? ?欧几里得相似度和余弦相似度是两种常用的衡量目标之间相似性的方法。欧几里得相似度以目标之间的绝对距离作为衡量标准，注重目标之间的差异，与目标在空间中的位置直接相关。而余弦相似度则以目标之间的夹角大小作为衡量标准，更加表现在前进趋势的差异。

? ? ? ?欧几里得相似度可以用来分析不同目标的绝对差异，从而判断它们之间的相似度和差异情况。它适用于需要关注目标之间的具体差异的情况。

? ? ? 余弦相似度则更注重目标从方向趋势上的区分，对特定坐标不敏感。它适用于需要关注目标的整体趋势和方向的情况。

文章来源:https://blog.csdn.net/lymake/article/details/135577127
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！