碳排放预测 | 基于ARIMA和GM(1,1)的碳排放预测(Matlab)
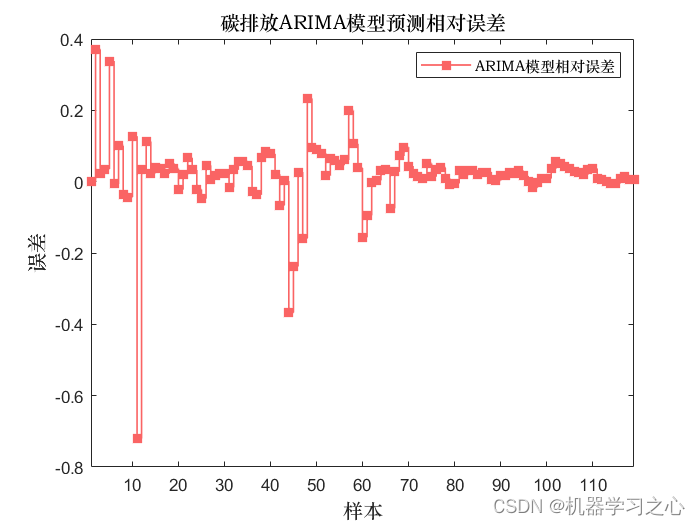
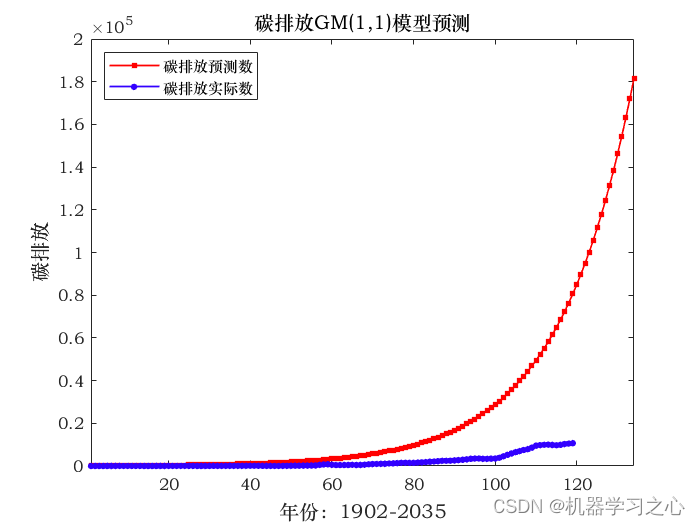
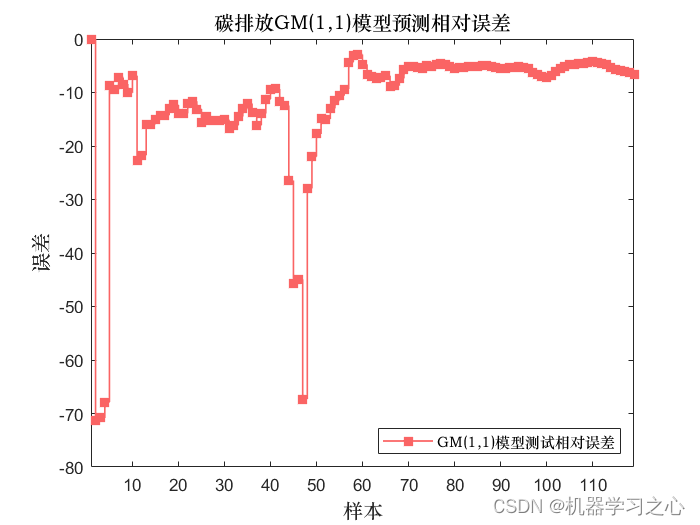
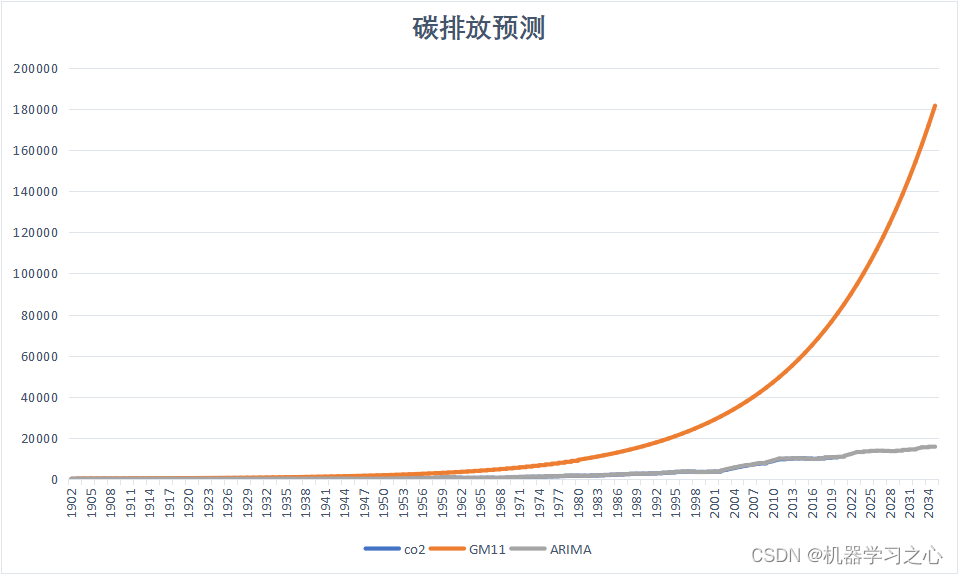
预测效果

基本介绍
基于ARIMA和GM(1,1)的碳排放预测(Matlab)
基于ARIMA(自回归移动平均模型)和GM(1,1)(灰色预测模型)的碳排放预测是一种常见的时间序列预测方法。
模型描述
ARIMA模型
ARIMA模型是一种经典的时间序列预测方法,它包含三个部分:自回归(AR)、差分(I)和移动平均(MA)。ARIMA模型的基本思想是通过对历史数据的分析来捕捉时间序列的趋势和周期性,从而进行未来值的预测。
ARIMA模型的建模过程通常包括以下步骤:
确定是否需要对原始数据进行平稳化处理,即检验时间序列数据是否具有平稳性。
如果数据不平稳,进行差分操作,直到数据平稳。
通过自相关函数(ACF)和偏自相关函数(PACF)的分析,确定ARIMA模型的阶数。
估计ARIMA模型的参数。
对模型进行诊断检验,确保模型的拟合程度和残差的随机性。
使用训练好的模型进行未来值的预测。
GM(1,1)模型
GM(1,1)模型是一种基于灰色系统理论的预测模型,适用于具有较少数据、无法建立充分统计模型的情况。该模型通过对原始数据进行累加、生成新序列,然后通过建立一阶差分方程来描述序列的发展趋势。
GM(1,1)模型的建模过程通常包括以下步骤:
累加原始数据得到累加生成序列。
建立一阶差分方程,通过参数估计求解出灰色模型的发展系数。
对模型进行检验,判断模型的拟合程度。
使用训练好的模型进行未来值的预测。
对于碳排放预测,您可以按照以下步骤进行操作:
收集碳排放的历史数据,确保数据是按照时间顺序排列的。
首先尝试使用ARIMA模型进行建模和预测,按照ARIMA模型的步骤进行操作。确定合适的ARIMA模型阶数,并训练模型。
进行ARIMA模型的诊断检验,评估模型的拟合优度。
如果ARIMA模型不满足要求,可以尝试使用GM(1,1)模型进行建模和预测。按照GM(1,1)模型的步骤进行操作,确定灰色模型的发展系数,并训练模型。
进行GM(1,1)模型的检验,评估模型的拟合优度。
使用训练好的模型进行未来的碳排放预测。
ARIMA和GM(1,1)模型都是基于历史数据进行预测,对于未来的碳排放预测仍会受到其他因素的影响,如政策变化、技术进步等。因此,预测结果仅供参考,并不一定完全准确。在实际应用中,还需综合考虑其他因素,进行综合分析和判断。
程序设计
- 完整程序和数据获取方式:私信博主回复基于ARIMA和GM(1,1)的碳排放预测(Matlab)。
参考资料
[1] http://t.csdn.cn/pCWSp
[2] https://download.csdn.net/download/kjm13182345320/87568090?spm=1001.2014.3001.5501
[3] https://blog.csdn.net/kjm13182345320/article/details/129433463?spm=1001.2014.3001.5501
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 交换机02_共享式&交换式
- 【C++干货铺】继承后的多态 | 抽象类
- react18框架笔记
- conda安装transformers包
- 集团数字化管理系统有哪些
- 高云GW1NSR-4C开发板M3核RT-Thread应用
- ChatGPT关键技术、发展方向与应用前景
- Spring Cloud Gateway请求路径修改指南:详解ServerWebExchange的完美解决方案及代码示例
- 【MySQL】一文看懂MySQL所有常见问题
- QTDAY1