动态规划之子序列问题

首先在开始本篇文章之前，我们必须要弄明白子序列，子序列不同于子数组和子串，子序列不要求是连续的，比如有数组vec = [1,3,5,4,8]，其中v1 = [1,4,8]就是vec的一个子序列，但是v1不是vec的子数组。常见的子数组、子串是有连续这个条件要求的，所有我们解题的时候一定要好好看清楚题目描述（是子序列还是子串）

下面题目的分类列表来自于代码随想录，题解也参照了代码随想录中的讲解(本文为博主的学习笔记，所以有部分是直接在代码随想录中截图的，大家多多支持开源作者，可以前往学习）

https://www.programmercarl.com/

1.子序列（不连续）

1.1最长上升子序列

dp数组的定义以及状态转移方程

解法一：动态规划

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size() <= 1) return nums.size();
        //dp[i]表示以nums[i]结尾的最长递增子序列的长度
        vector<int> dp(nums.size(), 1);
        int result = 1;
        for(int i = 1; i < nums.size(); i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if(dp[i] > result) result = dp[i];
        }
        return result;
    }
};

解法二：递归 + 记忆化搜索

class Solution {
public:
    int lengthOfLIS(vector<int> &nums) {
        int n = nums.size(), memo[n];
        memset(memo, 0, sizeof(memo)); // 本题可以初始化成 0，表示没有计算过
        function<int(int)> dfs = [&](int i) -> int {
            int &res = memo[i];
            if (res) return res;
            for (int j = 0; j < i; ++j)
                if (nums[j] < nums[i])
                    res = max(res, dfs(j));
            return ++res;
        };
        int ans = 0;
        for (int i = 0; i < n; ++i)
            ans = max(ans, dfs(i));
        return ans;
    }
};

---

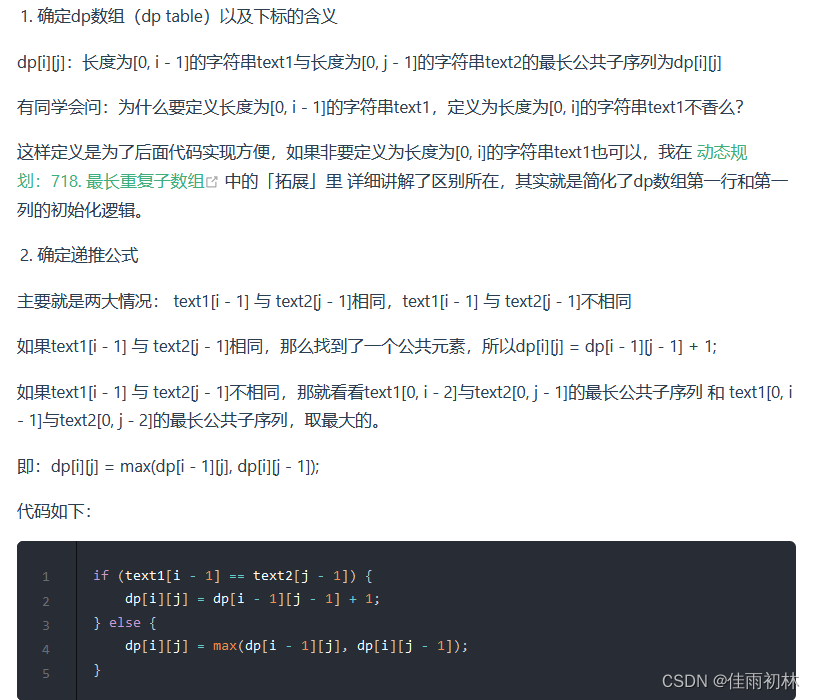
1.2最长公共子序列

dp数组含义的确立以及状态转移方程

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        //dp[i][j]表示以text1[i]&&text2[i]结尾序列的最长长度
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for(int i = 1; i <= text1.size(); i++){
            for(int j = 1; j <= text2.size(); j++){
                if(text1[i - 1] == text2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

---

1.3不相交的线

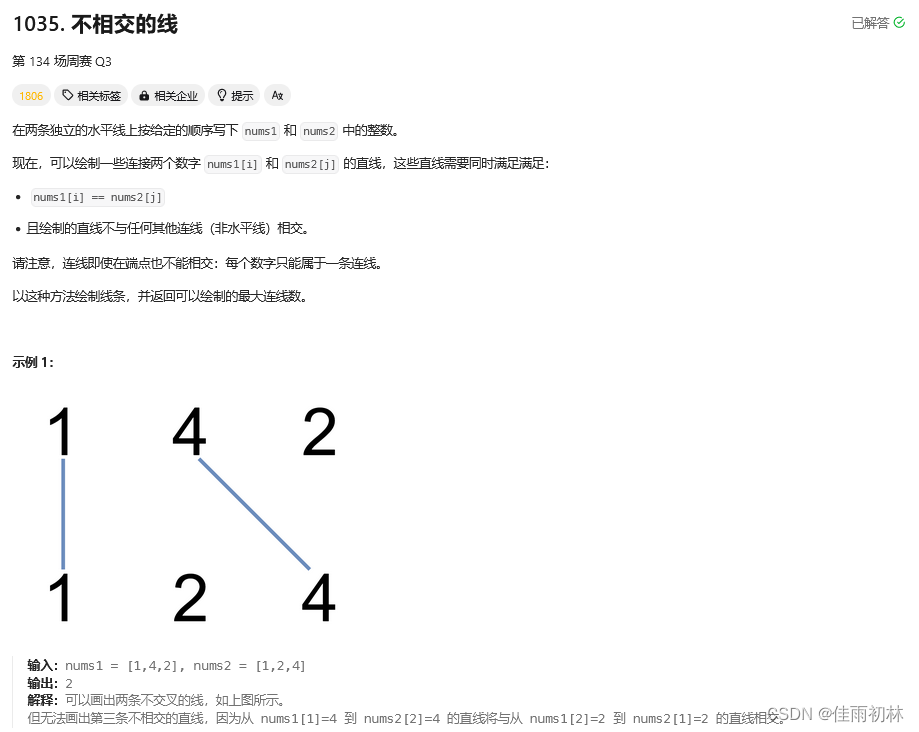一定要擅于分析题目，将一些题目信息充分利用，转化为我们熟悉的题目，比如这个题目：绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！，和上面的题目本质是一模一样的。

class Solution {
public:
    //剖析这个题目，其本质为找到最长公共子序列
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        //dp[i][j]的含义表示为：以nums1以下标i - 1结尾，nums2以下标j - 1结尾时的最长子序列长度
        //但是我们不要被误导了：nums1[i - 1]与nums2[j - 1]不一定相等！
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        for(int i = 1; i <= nums1.size(); i++){
            for(int j = 1; j <= nums2.size(); j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

---

2.子序列（连续）

2.1最长连续递增子序列

这个题目和题1.1的区别在于此出连续，也就是选择最长递增子数组的长度，好好对比两个题目的题解区别

dp数组的定义以及状态转移

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if(nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for(int i = 1; i < nums.size(); i++){
            if(nums[i] > nums[i - 1]){
                dp[i] =dp[i - 1] + 1;
            }
            result = max(result, dp[i]);
        }
        return result;
    }
};

---

2.2最长重复子数组

dp数组的定义以及状态转移方程

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        //dp[i][j]:表示以nums1[i-1]结尾&&以nums2[j-1]结尾的最长重复子数组长度
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;
        for(int i = 1; i <= nums1.size(); i++){
            for(int j = 1; j <= nums2.size(); j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if(dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

---

2.3最大子序和

dp数组的定义以及状态转移方程

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size() <= 1) return nums[0];
        //dp[i]表示以nums[i]结尾的连续子数组的最大值
        vector<int> dp(nums.size(), 0);
        dp[0] = nums[0];
        int result = dp[0];
        for(int i = 1; i < nums.size(); i++){
            if(nums[i] > 0) dp[i] = max(dp[i - 1] +nums[i], nums[i]);
            else dp[i] = max(nums[i],nums[i] + dp[i - 1]);
            result = max(result, dp[i]);
        }
        return result;
    }
};

---

3.编辑距离

3.1判断子序列

解法一：双指针解法（普通直接想到的解法）

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.length(), m = t.length();
        int i = 0, j = 0;
        while (i < n && j < m) {
            if (s[i] == t[j]) {
                i++;
            }
            j++;
        }
        return i == n;
    }
};

动态规划

class Solution {
public:
    //这个题目可以用最长公共子序列来做（最长的长度==s.size()则为true,否则为false）
    bool isSubsequence(string s, string t) {
        //dp[i][j]表示s截止s[i - 1](含s[i - 1])和t截止t[j - 1]的子串的最长子序列长度
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
        for(int i = 1; i <= s.size(); i++){
            for(int j = 1; j <= t.size(); j++){
                if(s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                //由于s是最简待匹配串，所以原本最长子序列中的代码（dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])）可以换成下面的;
                else dp[i][j] = dp[i][j - 1];
            }
        }
        return dp[s.size()][t.size()] == s.size();
    }
};

---

3.2不同的子序列

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

状态转移方程

class Solution {
public:
    //统计s的所有子序列中有多少个和t相同
    int numDistinct(string s, string t) {
        //dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
        //dp[i][0]表示以i - 1结尾的s得到空字符串这个子序列的个数（一定是1，为空全部清除就行）
        for(int i = 0; i < s.size(); i++) dp[i][0] = 1;
        //dp[0][j]无论如何都为0，空字符串无法有任何子序列（除开空字符串之外，所以dp[0][0]=0)
        for(int j = 1; j < t.size(); j++) dp[0][j] = 0;
        //开始动态规划的过程
        for(int i = 1; i <= s.size(); i++){
            for(int j = 1; j <= t.size(); j++){
                if(s[i - 1] == t[j - 1]){
                    //s:bagg t:bag 我们可以选择第一个g或者第二个取匹配，所以这里等于两者方法数量的和
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s.size()][t.size()];
    }
};

---

3.3两个字符串的删除操作

状态转移方程的确定

class Solution {
public:
    //求两个字符串的公共最长子序列
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector(word2.size() + 1, 0));
        for(int i = 1; i <= word1.size(); i++){
            for(int j = 1; j <= word2.size(); j++){
                if(word1[i - 1] == word2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()];
    }
};

---

3.4编辑距离

dp[i][j]:下标为0~i-1的word1子字符串,和以下标j-1为结尾的字符串word2的最近编辑距离

class Solution {
public:
    //dp[i][j]:下标为0~i-1的word1子字符串,和以下标j-1为结尾的字符串word2的最近编辑距离
    //状态转移方程：word1[i - 1] = word2[j - 1]，不用操作；不相等时需要进行增、删、换中的某一种操作
    //其中删除操作与增加操作等价。比如word1=ad, word2 =d， word1删除a或者word2添加a的操作次数的相等的
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        //初始化：dp[i][0] word1[0:i）需要操作i次才能边为空（此时的word2[0:0)是空的
        for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        //dp[0][j]初始化理由同上，需要操作j次才能为空
        for(int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        //开始动态规划
        for(int i = 1; i <= word1.size(); i++){
            for(int j = 1; j <= word2.size(); j++){
                if(word1[i - 1] == word2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1];
                }else{//不相等的时候需要操作
                    //删除操作：min(word1删除一个元素，word2删除一个元素) + 1 = min(dp[i][j - 1],dp[i - 1][j])+1
                    //替换操作：dp[i - 1][j - 1] + 1（上一个最近距离加上一次替换操作）
                    dp[i][j] = min(min(dp[i][j - 1],dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

---

4.回文

4.1回文子串

下面注释中的写法实现的过程是相同的，只是将逻辑进行了提取的

class Solution {
public:
    int countSubstrings(string s) {
        //isPalindrome[i][j] == true表示s[i:j]为回文串（闭区间）
        vector<vector<bool>> isPalindrome(s.size(), vector<bool> (s.size(), false));
        int count = 0;
        for(int i = s.size() - 1; i >= 0; i--){
            for(int j = i; j < s.size();j++){
                if(j == i){
                    isPalindrome[i][j] = true;
                }else if(j - i == 1){
                    isPalindrome[i][j] = (s[i] == s[j]);
                }else{
                    isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i + 1][j - 1]);
                }
                //如果是回文的话，那么增加数量
                if(isPalindrome[i][j]) count++;
            }
        }
        return count;

        // //dp[i][j] 表示s[i:j](左闭右闭)区间是否为回文串
        // vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        // int result = 0;
        // for(int i = s.size() - 1; i　>= 0; i--){
        //     for(int j = i; j < s.size();j++){
        //         if(s[i] == s[j]){
        //             if(j - i <= 1){
        //                 result++;
        //                 dp[i][j] = true;
        //             }else if(dp[i + 1][j - 1]){
        //                 result++;
        //                 dp[i][j] = true;
        //             }
        //         }
        //     }
        // }
        // return result;
    }
};

---

4.2最长回文子序列

一定要注意，这里是回文子序列，不是回文子串！！！子串是子序列，但是子序列并不一定是子串

dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

状态转移方程的确立

核心代码如下

if (s[i] == s[j]) {
    dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}

完整实现代码

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        for(int i = 0; i < s.size(); i++) dp[i][i] = 1;//单个字母为回文，且长度为1
        for(int i = s.size() - 1; i >= 0; i--){
            for(int j = i + 1; j < s.size(); j++){
                if(s[i] == s[j]){
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }else{
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][s.size() - 1];

    }
};