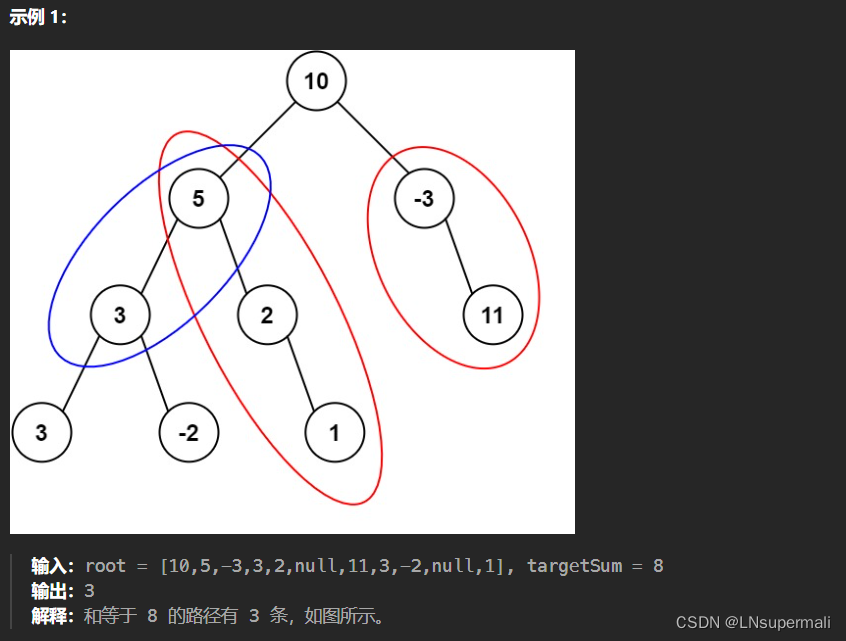
力扣437. 路径总和 III

Problem: 437. 路径总和 III

题目描述

思路

结合题目的特性我们可以想到利用二叉树的后序遍历，将某个节点和其相连的节点的值作为键添加到一个Map集合中，将等于该值存在的路径数作为值存入Map集合；我们从子节点可以推向根节点，最后统计集合中等于目标值的键对应的值即可

解题方法

1.定义变量count用于统计最终的路径数
2.调用并编写后续遍历函数

2.1当root为空时返回一个新的Map集合
2.2unordered_map<long, long> leftValues = dfs(root->left, sum);unordered_map<long, long> rightValues = dfs(root->right, sum);unordered_map<long, long> rootValues;即后续遍历，左-右-根；
2.3rootValues[(long )root->val] = (long )1;即表示当前rootValues集合中路径长度为root->val的初始化会有一条
2.4先遍历leftValues，得到新的键与值，新的键为当前的节点的值加上原来的键值,新的 值 为原来的值，接着检验rootValues中是否已经存在新的键，若存在则让新的值加上rootValues中的新的键对应的值，并将当前新的键与值存入rootValues中；以同样的方法处理rightValues
2.5最后遍历rootValues，若rootValues中的键和给定目标值相等，则count++

复杂度

时间复杂度:

$O(n^2)$;其中$n$为二叉树节点的个数

空间复杂度:

$O(n)$

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    //The final result
    int count = 0;
public:
    /**
     *
     * @param root The root of the binary tree
     * @param targetSum The target
     * @return int
     */
    int pathSum(TreeNode *root, int targetSum) {
        dfs(root, targetSum);
        return count;
    }

private:
    /**
     *
     * @param root The root of the binary tree
     * @param sum The target sum
     * @return unordered_map
     */
    unordered_map<long, long> dfs(TreeNode *root, int sum) {
        if (root == nullptr) {
            return unordered_map<long, long>();
        }
        unordered_map<long, long> leftValues = dfs(root->left, sum);
        unordered_map<long, long> rightValues = dfs(root->right, sum);
        unordered_map<long, long> rootValues;
        rootValues[(long )root->val] = (long )1;
        for (auto &entry: leftValues) {
            long newKey = entry.first + root->val;
            long newValue = entry.second;
            if (rootValues.count(newKey)) {
                newValue += rootValues[newKey];
            }
            rootValues[newKey] = newValue;
        }
        for (auto &entry: rightValues) {
            long newKey = entry.first + root->val;
            long newValue = entry.second;
            if (rootValues.count(newKey)) {
                newValue += rootValues[newKey];
            }
            rootValues[newKey] = newValue;
        }
        for (auto &entry: rootValues) {
            if (entry.first == sum) {
                count += entry.second;
            }
        }
        return rootValues;
    }
};